Entdecke die Welt der Symmetrieachsen: Formen, Beispiele und Zeichentechniken!

Symmetrieachsen sind Linien, die eine Figur in zwei spiegelbildlich gleiche Hälften teilen. Sie sind von großer Bedeutung in der Geometrie und helfen dabei, Symmetrien zu erkennen und zu analysieren. In diesem Artikel werden wir uns genauer mit dem Konzept der Symmetrieachsen befassen und ihre verschiedenen Eigenschaften untersuchen.

Was sind Symmetrieachsen und wie zeichnet man sie ein?

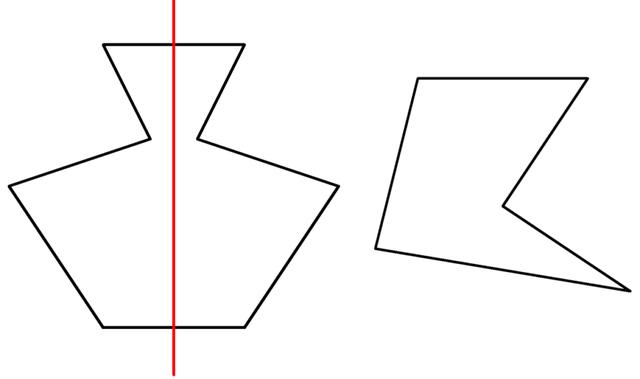
Definition der Symmetrieachse

Eine Symmetrieachse ist eine Linie, entlang der eine Figur oder ein Objekt gespiegelt werden kann, sodass beide Hälften identisch sind. Die Symmetrieachse teilt die Figur in zwei gleich große und spiegelbildliche Teile.

Beispiele für Figuren mit Symmetrieachsen

– Schmetterling: Wenn du die Flügel eines Schmetterlings genau in der Mitte faltest, sehen beide Hälften identisch aus. Die Faltlinie in der Mitte ist die Symmetrieachse.
– Haus: Ein Haus mit einer Tür in der Mitte und jeweils zwei Fenstern rechts und links kann entlang einer Linie an der Dachspitze gefaltet werden, sodass beide Seiten identisch sind. Diese Linie ist die Symmetrieachse.
– Laubblätter: Einige Laubblätter haben eine zentrale Mittelrippe als Symmetrieachse.
– Mond: Der Mond kann entlang einer vertikalen Achse gespiegelt werden, sodass beide Hälften identisch sind.

Einzeichnen einer Symmetrieachse

Um eine Symmetrieachse einzuziehen, musst du die Figur so falten oder spiegeln, dass beide Hälften übereinander liegen und deckungsgleich sind. Die Faltlinie oder Spiegelungslinie ist dann die Symmetrieachse. Es gibt auch Figuren mit mehreren Symmetrieachsen, wie zum Beispiel das Rechteck mit zwei Symmetrieachsen und das Quadrat mit vier Symmetrieachsen.

Symmetrieachsen: Definition, Beispiele und Einzeichnung

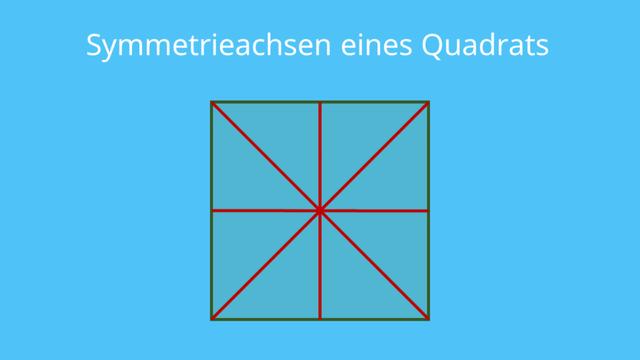
Definition

Eine Symmetrieachse ist eine Linie, entlang der eine Figur in zwei spiegelbildliche Hälften geteilt werden kann. Die beiden Hälften sind dabei genau gleich groß und passen perfekt aufeinander. Die Symmetrieachse wird auch als Spiegelachse bezeichnet, da sie die eine Hälfte der Figur auf die andere Hälfte spiegelt.

Beispiele

– Ein Schmetterling hat eine Symmetrieachse in der Mitte seiner Flügel. Wenn man die Flügel an dieser Achse faltet, sehen beide Hälften genau gleich aus.
– Ein Haus mit einer Tür in der Mitte und jeweils zwei Fenstern rechts und links hat eine Symmetrieachse entlang der Dachspitze. Wenn man das Haus entlang dieser Achse faltet, sind beide Seiten identisch.
– Manche Laubblätter haben ebenfalls eine Symmetrieachse. Wenn man das Blatt entlang dieser Achse faltet, sind beide Hälften gleich.
– Ein Quadrat hat vier Symmetrieachsen: Eine horizontale, eine vertikale und zwei diagonale Achsen. Diese teilen das Quadrat in vier spiegelbildliche Viertel.
– Ein Kreis hat unendlich viele Symmetrieachsen, die alle durch seinen Mittelpunkt verlaufen.

Einzeichnung einer Symmetrieachse

Um eine Symmetrieachse einzuziehen, muss man prüfen, ob eine Figur tatsächlich achsensymmetrisch ist. Dazu kann man die Figur so falten, dass die beiden Hälften genau gleich groß sind und übereinander liegen. Die Faltlinie entspricht dann der Symmetrieachse. Man kann sich die Symmetrieachse auch als Spiegel vorstellen, der eine Hälfte der Figur auf die andere spiegelt.

In der Mathematik gibt es viele verschiedene Figuren mit Symmetrieachsen. Rechtecke haben beispielsweise zwei Symmetrieachsen, während ein Quadrat vier Symmetrieachsen hat. Auch andere Vierecke können symmetrisch zueinander sein. Um herauszufinden, wie viele Symmetrieachsen eine Figur hat, muss man ihre Eigenschaften untersuchen.

Im Alltag begegnen uns zahlreiche Formen mit Symmetrieachsen. Indem wir diese erkennen und einzeichnen, können wir das Konzept der Symmetrie besser verstehen und anwenden.

Figuren mit Symmetrieachsen: Erklärung und Anwendung

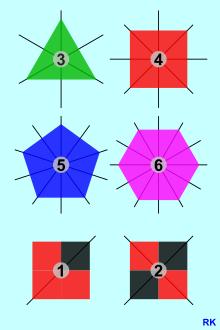
Was ist eine Symmetrieachse?

Eine Symmetrieachse ist eine Linie, die eine Figur in zwei gleich große und spiegelverkehrte Hälften teilt. Diese Hälften passen perfekt aufeinander und sind deckungsgleich oder kongruent. Die Symmetrieachse kann auch als Spiegelachse bezeichnet werden, da sie die Figur wie ein Spiegel spiegelt.

Welche Figuren haben Symmetrieachsen?

Verschiedene Figuren können Symmetrieachsen haben. Einige Beispiele sind:
– Schmetterling: Wenn du die Flügel eines Schmetterlings in der Mitte faltest, sehen beide Hälften genau gleich aus.
– Haus: Wenn du an der Dachspitze eines Hauses eine Linie nach unten ziehst, kannst du die beiden Seiten an dieser Linie falten und sie sehen dann genau gleich aus.
– Laubblätter: Bei einigen Laubblättern kannst du eine Symmetrieachse einzeichnen.
– Mond: Auch beim Mond kannst du eine Symmetrieachse finden.

Wie kannst du eine Symmetrieachse einzeichnen?

Um eine Symmetrieachse einzuziehen, musst du prüfen, ob eine Figur tatsächlich achsensymmetrisch ist. Du kannst dies tun, indem du die Figur so faltest, dass beide Hälften genau gleich groß sind und übereinander liegen. Die Faltlinie ist dann die Symmetrieachse. Alternativ kannst du dir die Symmetrieachse auch als Spiegel vorstellen, der einen Teil der Figur genau auf den anderen spiegelt.

Symmetrieachsen in der Geometrie: Bedeutung und Zeichnung

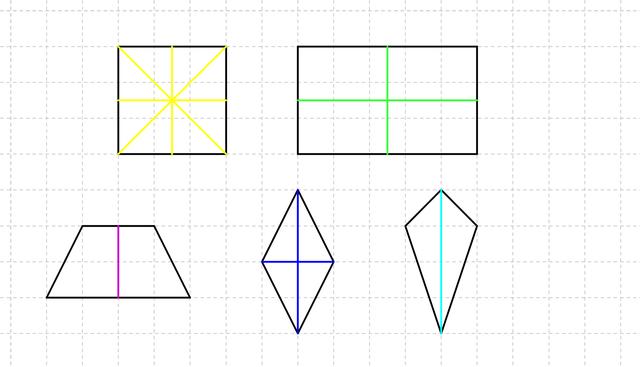
Was ist eine Symmetrieachse?

Eine Symmetrieachse ist eine Linie, an der eine Figur in zwei gleiche Hälften gespiegelt werden kann. Diese Hälften sind deckungsgleich oder kongruent zueinander. Die Symmetrieachse wird auch als Spiegelachse bezeichnet, da sie die Figur wie ein Spiegel spiegelt.

Figuren mit Symmetrieachsen

Verschiedene Figuren können Symmetrieachsen haben. Ein Beispiel dafür ist der Schmetterling, dessen Flügel symmetrisch sind und eine Faltlinie in der Mitte haben. Auch ein Haus mit einer Tür in der Mitte und Fenstern auf beiden Seiten hat eine Symmetrieachse entlang des Daches. Laubblätter und der Mond können ebenfalls Symmetrieachsen haben.

Einzeichnen einer Symmetrieachse

Um eine Symmetrieachse einzuziehen, muss man die Figur so falten, dass beide Hälften genau gleich aussehen und übereinander liegen. Die Faltlinie entspricht dann der Symmetrieachse. Es gibt auch Figuren mit mehr als einer Symmetrieachse, wie zum Beispiel das Rechteck mit zwei Symmetrieachsen oder das Quadrat mit vier Symmetrieachsen. Ein Kreis hat unendlich viele Symmetrieachsen, die alle durch seinen Mittelpunkt gehen.

Zusammenfassend kann man sagen, dass eine Symmetrieachse in der Geometrie eine Linie ist, an der eine Figur in zwei gleiche Hälften gespiegelt werden kann. Man kann sie einzeichnen, indem man die Figur so faltet, dass beide Hälften übereinander liegen. Verschiedene Figuren haben Symmetrieachsen, wie der Schmetterling, das Haus oder auch geometrische Formen wie Rechtecke und Kreise.

Alles über Symmetrieachsen: Beispiele und Vorgehensweise

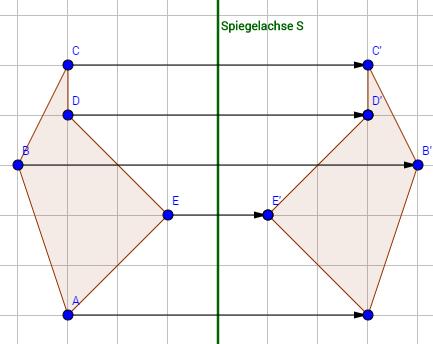
Beispiele für Figuren mit Symmetrieachsen:

– Schmetterling: Wenn du die Flügel eines Schmetterlings in der Mitte faltest, sehen beide Hälften genau gleich aus. Die Faltlinie in der Mitte ist die Symmetrieachse.
– Haus: Ein Haus mit einer Tür in der Mitte und jeweils zwei Fenstern rechts und links kann entlang einer Linie an der Dachspitze gefaltet werden, sodass beide Seiten identisch sind. Die Linie ist die Symmetrieachse.
– Laubblätter: Einige Laubblätter haben eine Symmetrieachse, entlang derer sie gefaltet werden können, um identische Hälften zu erzeugen.
– Mond: Der Mond hat eine Symmetrieachse, entlang derer er gespiegelt werden kann.

Vorgehensweise zum Einzeichnen einer Symmetrieachse:

1. Prüfe, ob die Figur achsensymmetrisch ist, indem du sie so faltest, dass beide Hälften genau gleich groß sind und übereinander liegen.
2. Zeichne die Symmetrieachse an der Faltlinie ein.
3. Beachte, dass eine Spiegelachse oder Symmetrieachse eine Figur in zwei Teile teilt, die genau gleich groß und deckungsgleich sind.

In der Mathematik gibt es verschiedene Figuren mit unterschiedlicher Anzahl von Symmetrieachsen. Rechtecke haben beispielsweise zwei Symmetrieachsen (von rechts nach links oder von oben nach unten), während Quadrate vier Symmetrieachsen haben (auch entlang der Diagonalen). Gleichseitige Dreiecke haben drei Symmetrieachsen, wenn alle Seiten gleich lang sind. Ein Kreis hat unendlich viele Symmetrieachsen, da sie alle durch den Mittelpunkt gehen.

Es gibt auch Figuren, die keine typische Form haben und symmetrisch sein können oder auch nicht. Manche Figuren können sogar mehr als eine Symmetrieachse haben.

Die Bedeutung von Symmetrieachsen in der Mathematik

Symmetrieachsen sind ein wichtiges Konzept in der Mathematik und haben verschiedene Anwendungen. Hier sind einige Bedeutungen von Symmetrieachsen:

– Symmetrieachsen helfen uns dabei, symmetrische Figuren zu erkennen und zu analysieren. Indem wir eine Symmetrieachse einzeichnen, können wir die Figur in zwei identische Hälften teilen und ihre Eigenschaften untersuchen.
– In der Geometrie ermöglichen uns Symmetrieachsen, bestimmte Berechnungen oder Konstruktionen zu vereinfachen. Zum Beispiel können wir die Länge oder Fläche einer symmetrischen Figur berechnen, indem wir nur eine Hälfte betrachten und sie dann verdoppeln.
– Symmetrieachsen spielen auch in der Algebra eine Rolle. Wenn wir eine Funktion graphisch darstellen, können wir anhand ihrer Symmetrien Rückschlüsse auf ihre Gleichungen ziehen. Eine Funktion mit einer vertikalen Symmetrieachse hat beispielsweise eine spezielle Formel.
– In der Kombinatorik können Symmetrien verwendet werden, um bestimmte Probleme zu lösen. Indem man die Anzahl der symmetrischen Anordnungen einer Figur bestimmt, kann man beispielsweise die Anzahl der Möglichkeiten berechnen, wie sich Objekte auf einem Schachbrett anordnen lassen.

Symmetrieachsen sind also nicht nur ein visuelles Konzept, sondern haben auch mathematische Bedeutung und Anwendungen in verschiedenen Bereichen der Mathematik.

In der Mathematik sind Symmetrieachsen imaginäre Linien, die eine Figur in zwei gleichartige Hälften teilen. Sie spielen eine wichtige Rolle bei der Analyse und dem Verständnis von geometrischen Formen und Mustern. Symmetrieachsen helfen uns, Muster zu erkennen, Strukturen zu verstehen und mathematische Probleme zu lösen. Durch die Identifizierung von Symmetrieachsen können wir die Ähnlichkeiten und Unterschiede zwischen verschiedenen Objekten besser erfassen und diese Informationen in vielen Bereichen wie Kunst, Architektur und Naturwissenschaften nutzen.