Eine ganzrationale Funktion ist eine mathematische Funktion, deren Ausdruck aus Polynomen besteht. Sie spielt eine wichtige Rolle in der Mathematik und wird oft zur Modellierung von realen Phänomenen verwendet. In diesem Artikel werden wir uns näher mit ganzrationalen Funktionen befassen und ihre Eigenschaften untersuchen.
Ganzrationale Funktionen: Definition, Eigenschaften und Beispiele
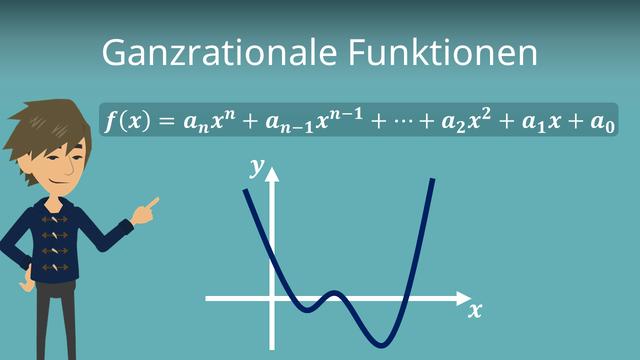
Definition
Ganzrationale Funktionen, auch Polynomfunktionen genannt, sind Funktionen, die aus der Summe einzelner polynomieller Bestandteile in einer Variablen bestehen. Im Gegensatz zu gebrochen rationalen Funktionen enthalten sie keine Brüche.
Eigenschaften
– Der Grad einer ganzrationalen Funktion wird durch den höchsten Exponenten bestimmt. Eine Funktion 4. Grades hat beispielsweise den höchsten Exponenten 4.
– Die Koeffizienten vor den Potenzen werden als Koeffizienten bezeichnet. Der Faktor vor der höchsten Potenz wird Leitkoeffizient genannt.
– Ganzrationale Funktionen mit nur dem Leitkoeffizienten und einer Potenz werden als Potenzfunktionen bezeichnet.
– Konstante Funktionen sind Polynomfunktionen 0. Grades, da sie unabhängig von x sind.
Beispiele
1. Lineare Funktion: f(x) = 2x + 1
– Grad: 1
– Leitkoeffizient: 2
2. Quadratische Funktion: f(x) = x^2 + 3x – 5
– Grad: 2
– Leitkoeffizient: 1
3. Kubische Funktion: f(x) = x^3 – 4x^2 + x + 2
– Grad: 3
– Leitkoeffizient: 1
4. Ganzrationale Funktion 4. Grades: f(x) = 3x^4 – 2x^3 + x^2 – 5x + 1
– Grad: 4
– Leitkoeffizient: 3
Unterscheidung zu Nicht-Polynomfunktionen
Nicht alle Funktionen sind ganzrationale Funktionen. Einige Beispiele für nicht ganzrationale Funktionen sind trigonometrische Funktionen wie Sinus oder Kosinus, Exponentialfunktionen oder Logarithmusfunktionen. Diese unterscheiden sich von ganzrationalen Funktionen in ihrem Funktionsverhalten und ihrer Definition.
Polynomfunktionen: Aufbau und Eigenschaften erklärt
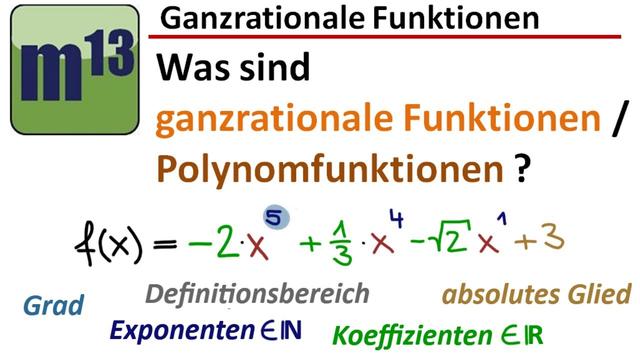
Eine Polynomfunktion ist eine ganzrationale Funktion, die aus der Summe einzelner polynomieller Bestandteile besteht. Je nach den Werten, die für die Variablen eingesetzt werden, erhält man verschiedene Polynomfunktionen mit unterschiedlichen Funktionsgraphen.
Grad der Polynomfunktion
Der Grad einer Polynomfunktion wird durch den höchsten Exponenten bestimmt. Zum Beispiel hat eine Funktion 4. Grades den höchsten Exponenten von 4. Der Grad entscheidet darüber, wie die Funktion global betrachtet aussieht und wie sie sich an den Rändern des Definitionsbereichs verhält.
Koeffizienten einer Polynomfunktion
Die Faktoren vor den Potenzen in einer Polynomfunktion werden als Koeffizienten bezeichnet. Der Faktor vor der höchsten Potenz wird als Leitkoeffizient bezeichnet. Ganzrationale Funktionen, die nur aus dem Leitkoeffizienten und einer Potenz bestehen, werden auch als Potenzfunktionen bezeichnet.
Eigenschaften von Polynomfunktionen
– Lineare Funktionen sind ganzrationale Funktionen 1. Grades.
– Quadratische Funktionen sind ganzrationale Funktionen vom Grad 2 und beschreiben Parabeln im Koordinatensystem.
– Kubische Funktionen sind ganzrationale Funktionen 3. Grades.
– Für ganzrationale Funktion vom Grad 4 gibt es keinen speziellen Namen mehr.
Symmetrie und Grenzwerte von Polynomfunktionen
– Eine Polynomfunktion ist achsensymmetrisch zur x-Achse, wenn sie nur gerade Exponenten enthält.
– Eine Polynomfunktion ist punktsymmetrisch zum Ursprung, wenn sie nur ungerade Exponenten enthält.
– Die Grenzwerte einer Polynomfunktion hängen vom Grad der Funktion und dem Vorzeichen des Leitkoeffizienten ab.
Berechnung von Nullstellen und Extrempunkten
– Für die Berechnung der Nullstellen einer Polynomfunktion gibt es verschiedene Methoden, abhängig vom Grad der Funktion. Im Allgemeinen gilt, dass die Anzahl der reellen Nullstellen kleiner oder gleich dem Grad der Funktion ist.
– Die Anzahl der Extrempunkte einer Polynomfunktion ist maximal gleich dem Grad der Funktion. Zur Bestimmung der Extrempunkte berechnet man die Nullstellen der Ableitungsfunktion.
Dies sind einige grundlegende Eigenschaften und Berechnungsmethoden für Polynomfunktionen. Es gibt noch viele weitere Aspekte zu entdecken und zu erforschen.
Ganzrationale Funktionen: Nullstellen und Grenzwerte verstehen
Ganzrationale Funktionen sind Polynomfunktionen, die aus einzelnen polynomiellen Bestandteilen in einer Variablen bestehen. Je nach den Werten, die für die Variablen eingesetzt werden, ergeben sich verschiedene Funktionsgraphen. Die höchste Potenz in einer ganzrationalen Funktion wird als Ordnung bezeichnet. Die Koeffizienten vor den Potenzen werden als Koeffizienten bezeichnet und der Faktor vor der höchsten Potenz wird als Leitkoeffizient bezeichnet.
Es gibt verschiedene Arten von ganzrationalen Funktionen. Lineare Funktionen haben eine Exponente von 1 und beschreiben eine Gerade im Koordinatensystem. Quadratische Funktionen haben einen Exponente von 2 und beschreiben Parabeln. Kubische Funktionen haben einen Exponente von 3 und beschreiben spezielle Kurven im Koordinatensystem. Ganzrationale Funktionen vom Grad 4 haben keinen besonderen Namen mehr.
Ganzrationale Funktionen können entweder achsensymmetrisch zur x-Achse sein, wenn sie nur gerade Exponente enthalten, oder punktsymmetrisch zum Ursprung sein, wenn sie nur ungerade Exponente enthalten. Wenn eine ganzrationale Funktion sowohl gerade als auch ungerade Exponente enthält, ist sie weder punktsymmetrisch noch achsensymmetrisch.
Die Nullstellen einer Polynomfunktion können auf verschiedene Weise berechnet werden, abhängig vom Grad der Funktion. Bei linearen und quadratischen Funktionen gibt es einfache Lösungsformeln wie die Mitternachts- oder pq-Formel. Bei Polynomfunktionen mit höherem Grad kann eine Polynomdivision oder das Ausklammern verwendet werden, sofern eine Nullstelle bekannt ist.
Ganzrationale Funktionen haben oft mehrere Extrempunkte, wie Minima, Maxima oder Sattelpunkte. Die Anzahl der reellen Nullstellen einer ganzrationalen Funktion ist kleiner oder gleich dem Grad der Funktion.
Es gibt auch gebrochen rationale Funktionen, die als Bruch aus zwei Polynomen definiert sind. Diese Funktionen haben einen Funktionsgraphen in Form einer waagrechten Geraden oder einer Geraden mit Steigung und y-Achsenabschnitt.
Um die Nullstellen und Grenzwerte von ganzrationalen Funktionen zu verstehen, können verschiedene Schritte durchgeführt werden. Dazu gehört das Berechnen der Ableitung, um die Extrempunkte zu bestimmen, sowie das Einsetzen von Werten in die ursprüngliche Funktion, um die zugehörigen y-Koordinaten zu erhalten. Die Art der Extrempunkte kann durch weitere Untersuchungen bestimmt werden.
Unterschied zwischen ganzrationalen und gebrochen rationalen Funktionen
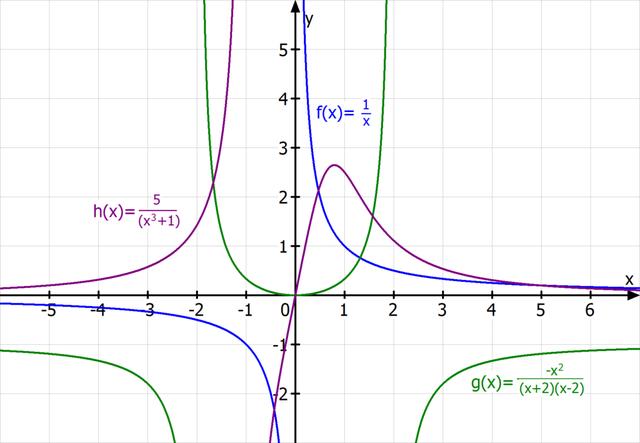
Ganzrationale Funktionen sind Polynomfunktionen, die aus der Summe einzelner polynomieller Bestandteile in einer Variablen bestehen. Sie werden immer in Abgrenzung zu den gebrochen rationalen Funktionen definiert. Bei ganzrationalen Funktionen gibt es verschiedene Begriffe, die man kennen sollte. Der höchste Exponent in der Funktion entscheidet über das Aussehen der Funktion und ihr Verhalten an den Rändern des Definitionsbereichs. Die Faktoren vor den Potenzen werden Koeffizienten genannt und der Faktor vor der höchsten Potenz wird als Leitkoeffizient bezeichnet.
Im Gegensatz dazu bestehen gebrochen rationale Funktionen aus einem Bruch zweier Polynome. Der Funktionsterm ist also ein Bruch aus zwei Polynomen. Gebrochen rationale Funktionen haben oft waagrechte Asymptoten, da sich die Funktionswerte bestimmten Grenzwerten annähern, wenn x gegen positive oder negative Unendlichkeit strebt.
Der Hauptunterschied zwischen ganzrationalen und gebrochen rationalen Funktionen liegt also in ihrer Struktur und ihren Eigenschaften. Ganzrationale Funktionen haben keine Brüche im Funktionsterm und können verschiedene Symmetrien aufweisen, abhängig vom Grad der Funktion. Gebrochen rationale Funktionen hingegen bestehen aus einem Bruch zweier Polynome und haben oft waagrechte Asymptoten.
Zusammenfassend kann man sagen, dass ganzrationale Funktionen Polynomfunktionen sind, während gebrochen rationale Funktionen aus einem Bruch zweier Polynome bestehen.
Symmetrie und Grenzwerte bei ganzrationalen Funktionen
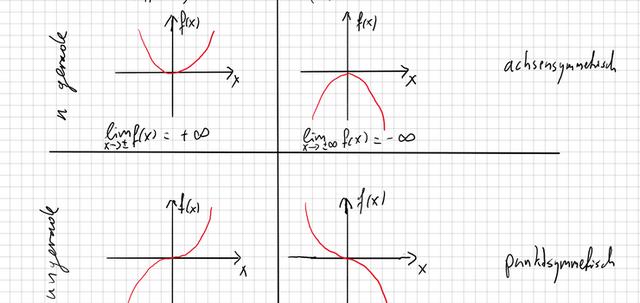
Eine wichtige Eigenschaft von ganzrationalen Funktionen ist ihre Symmetrie. Je nach Grad der Funktion und den Exponenten in ihrer Funktionsgleichung können sie achsensymmetrisch zur x-Achse oder punktsymmetrisch zum Ursprung sein.
– Achsensymmetrie zur x-Achse: Eine ganzrationale Funktion ist genau dann achsensymmetrisch zur x-Achse, wenn sie nur gerade Exponenten in ihrer Funktionsgleichung enthält. Das bedeutet, dass alle negativen Vorzeichen sich gegenseitig aufheben. Ein Beispiel hierfür ist die Funktion f(x) = x^4 – 2x^2 + 3.
– Punktsymmetrie zum Ursprung: Eine ganzrationale Funktion ist punktsymmetrisch zum Ursprung, wenn sie nur ungerade Exponenten in ihrer Funktionsgleichung enthält. Das bedeutet, dass die Funktionswerte für positive und negative x-Werte gleich sind. Ein Beispiel hierfür ist die Funktion g(x) = x^3 – 4x.
Es gibt auch Fälle, in denen eine ganzrationale Funktion weder punktsymmetrisch noch achsensymmetrisch ist. Dies tritt auf, wenn die Funktionsgleichung sowohl gerade als auch ungerade Exponenten enthält.
Die Grenzwerte einer ganzrationalen Funktion hängen ebenfalls vom Grad der Funktion ab und vom Vorzeichen des Leitkoeffizienten, also dem Koeffizienten vor der höchsten Potenz in der Funktionsgleichung.
– Ganzrationale Funktionen mit geradem Exponenten ähneln global betrachtet einer quadratischen Funktion. Die beiden Parabel-Äste laufen in die gleiche Richtung. Es gibt zwei Möglichkeiten: Entweder verläuft der Funktionsgraph nach oben oder nach unten, abhängig vom Vorzeichen des Leitkoeffizienten.
– Ganzrationale Funktionen mit ungeradem Grad zeigen global betrachtet Ähnlichkeit mit dem Graphen einer Funktion 3. Grades. Das Vorzeichen des Leitkoeffizienten bestimmt das Verhalten im Unendlichen. Wenn der Leitkoeffizient positiv ist, steigt die Funktion im Unendlichen an und wenn er negativ ist, fällt die Funktion im Unendlichen ab.
Diese Eigenschaften von Symmetrie und Grenzwerten sind wichtig, um den Verlauf und das Verhalten von ganzrationalen Funktionen besser zu verstehen und analysieren zu können.
Berechnung von Nullstellen und Extrempunkten bei Polynomfunktionen
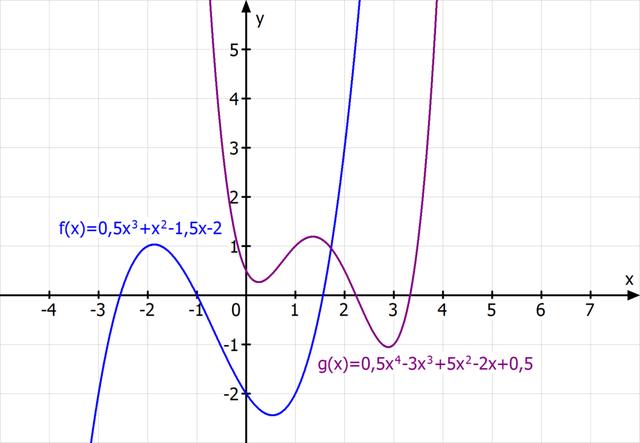
Die Berechnung von Nullstellen und Extrempunkten bei Polynomfunktionen kann mit verschiedenen Methoden erfolgen. Hier sind die Schritte, die du befolgen kannst:
1. Nullstellen berechnen:
– Für lineare Funktionen (Grad 1) kannst du einfach den Funktionswert gleich null setzen und nach x auflösen.
– Bei quadratischen Funktionen (Grad 2) kannst du entweder die Mitternachtsformel oder die pq-Formel verwenden, um die Nullstellen zu berechnen.
– Für Funktionen höheren Grades gibt es keine allgemeine Lösungsformel mehr. Du kannst jedoch versuchen, durch Ausklammern oder eine Polynomdivision eine Nullstelle zu finden und dann den Prozess für das verbleibende Polynom wiederholen.
2. Extrempunkte bestimmen:
– Um die Extrempunkte einer ganzrationalen Funktion zu finden, musst du zuerst die Ableitung der Funktion bilden.
– Setze die Ableitung gleich null und löse nach x auf, um die x-Koordinaten der Extrempunkte zu erhalten.
– Um die y-Koordinate der Extrempunkte zu bestimmen, setze diese x-Werte in den ursprünglichen Funktionsterm ein.
3. Bestimme die Art der Extrempunkte:
– Um festzustellen, ob es sich bei einem Extrempunkt um ein Maximum, Minimum oder einen Sattelpunkt handelt, betrachte das Verhalten der Funktion vor und nach dem Extrempunkt.
– Wenn sich das Vorzeichen der Steigung ändert (von positiv zu negativ oder umgekehrt), handelt es sich um ein Maximum oder Minimum.
– Wenn die Steigung vor und nach dem Extrempunkt gleich bleibt, handelt es sich um einen Sattelpunkt.
Es ist wichtig zu beachten, dass die Anzahl der reellen Nullstellen einer Polynomfunktion kleiner oder gleich dem Grad der Funktion ist. Das bedeutet, dass eine ganzrationale Funktion vom Grad 5 höchstens 5 Nullstellen haben kann.
Zusammenfassend können wir sagen, dass die Berechnung von Nullstellen und Extrempunkten bei Polynomfunktionen je nach Grad der Funktion unterschiedliche Methoden erfordert. Bei linearen und quadratischen Funktionen gibt es einfache Lösungsformeln, während für Funktionen höheren Grades keine allgemeine Lösungsformel existiert. In diesen Fällen musst du entweder Ausklammern oder eine Polynomdivision durchführen, um Nullstellen zu finden. Die Bestimmung der Extrempunkte erfordert die Ableitung der Funktion und das Lösen von Gleichungen.
Zusammenfassend sind ganzrationale Funktionen Polynomfunktionen, die sowohl ganze Zahlen als auch rationale Zahlen als Exponenten haben können. Sie sind durch eine allgemeine Formel dargestellt und weisen charakteristische Merkmale wie Symmetrie und Verhalten im Unendlichen auf. Ganzrationale Funktionen finden in verschiedenen mathematischen Anwendungen Anwendung und ermöglichen es uns, komplexe Phänomene zu analysieren und vorherzusagen.