Eine Symmetrieachse ist eine Linie, um die ein Objekt auf sich selbst abgebildet werden kann. Sie teilt das Objekt in zwei spiegelbildliche Hälften. Diese Achse spielt eine wichtige Rolle in der Geometrie und anderen Bereichen wie Kunst und Natur. In diesem Artikel werden wir die Bedeutung und Eigenschaften einer Symmetrieachse genauer untersuchen.
Was ist eine Symmetrieachse und wie funktioniert sie?
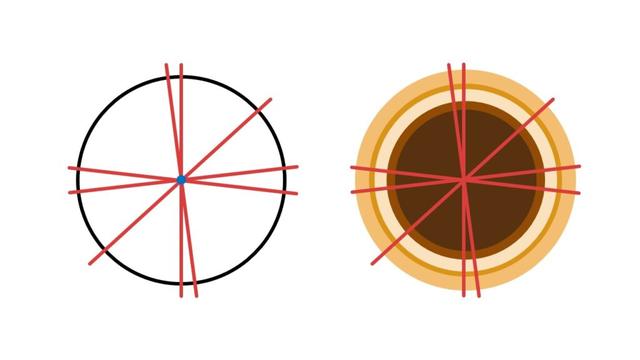
Eine Symmetrieachse ist eine imaginäre Linie, an der eine Figur gespiegelt wird, um Achsensymmetrie zu erzeugen. Diese Achse teilt die Figur in zwei Hälften, die genau übereinstimmen. Durch das Spiegeln entsteht eine Kopie der Originalfigur auf der anderen Seite der Achse.
Um eine Symmetrieachse zu finden, kann man verschiedene Methoden verwenden. Eine Möglichkeit ist es, die Figur auf einem karierten Papier zu zeichnen und vertikale oder horizontale Linien als Orientierungshilfe zu verwenden. Durch das Spiegeln der Figur an diesen Linien kann man die Symmetrieachse bestimmen.
Es gibt verschiedene Arten von Symmetrieachsen. Bei einer Punktachse wird die Figur an einem bestimmten Punkt gespiegelt. Bei einer Spiegelachse wird die Figur entlang einer geraden Linie gespiegelt. Je nach Form der Figur können unterschiedlich viele Symmetrieachsen vorhanden sein.
Ein bekanntes Beispiel für eine Symmetrieachse ist die y-Achse in einem Koordinatensystem. Wenn eine Funktion achsensymmetrisch zur y-Achse ist, bedeutet dies, dass f(x) = f(-x) gilt. Das bedeutet, dass jeder Punkt auf der Kurve der Funktion einen entsprechenden Punkt hat, der auf der anderen Seite der y-Achse liegt.
Insgesamt spielen Symmetrieachsen eine wichtige Rolle bei der Bestimmung von Achsensymmetrie und dem Verständnis von symmetrischen Figuren und Funktionen.
Die Bedeutung einer Symmetrieachse und ihre Anwendung
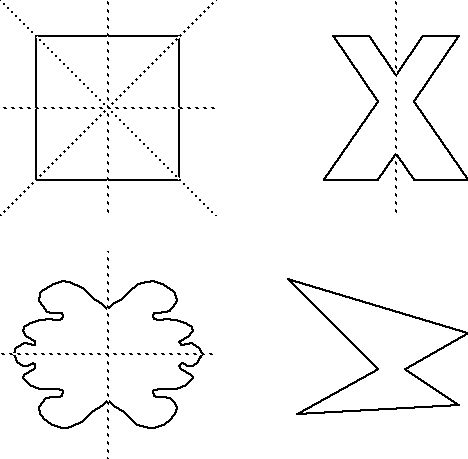
Eine Symmetrieachse ist eine imaginäre Linie, entlang der eine Figur gespiegelt wird und die beiden Hälften der Figur genau übereinstimmen. Die Symmetrieachse wird auch als Spiegelachse bezeichnet. Sie spielt eine wichtige Rolle bei der Betrachtung von symmetrischen Figuren und Funktionen.
Eine Symmetrieachse ermöglicht es uns, bestimmte Eigenschaften einer Figur oder Funktion zu erkennen. Durch das Spiegeln entstehen identische Teile auf beiden Seiten der Achse. Dies kann uns helfen, die Form oder Struktur einer Figur besser zu verstehen oder mathematische Zusammenhänge bei Funktionen zu erkennen.
Symmetrieachsen werden in verschiedenen Bereichen angewendet. In der Geometrie werden sie verwendet, um symmetrische Figuren wie Quadrate, Rechtecke oder Dreiecke zu beschreiben. Durch das Identifizieren von Symmetrieachsen können wir die Anzahl und Position dieser Achsen bestimmen.
In der Mathematik werden Symmetrien auch bei Funktionen betrachtet. Eine Symmetrie zur y-Achse bedeutet, dass die Funktion achsensymmetrisch ist und sich an der y-Achse spiegeln lässt. Dies kann dazu beitragen, bestimmte Eigenschaften einer Funktion wie den Scheitelpunkt oder den Verlauf des Graphen zu bestimmen.
Die Bedeutung einer Symmetrieachse liegt also darin, dass sie uns hilft, Muster und Strukturen in Figuren und Funktionen zu erkennen und mathematische Zusammenhänge besser zu verstehen. Sie ist ein wichtiges Konzept in der Geometrie und der Analysis und findet Anwendung in verschiedenen Bereichen wie Kunst, Design und Naturwissenschaften.
Erklärung der Symmetrieachse und ihre Eigenschaften
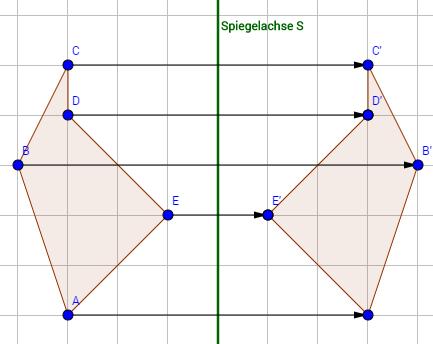
Eine Symmetrieachse ist eine Linie, entlang der eine Figur gespiegelt wird und die zwei identische Hälften erzeugt. Sie wird auch als Spiegelachse bezeichnet. Eine Figur ist achsensymmetrisch, wenn sie sich an einer Symmetrieachse spiegeln lässt und die gespiegelte Hälfte genau mit der anderen Hälfte übereinstimmt.
Hier sind einige Eigenschaften der Symmetrieachsen:
1. Die Symmetrieachse kann vertikal oder horizontal verlaufen. Bei einer vertikalen Symmetrieachse spiegelt sich die Figur nach links und rechts, während bei einer horizontalen Symmetrieachse die Figur nach oben und unten gespiegelt wird.
2. Ein Quadrat hat immer vier Symmetrieachsen. Zwei verlaufen durch die Mitte des Quadrats und teilen es in zwei identische Hälften, während die anderen beiden durch die Ecken des Quadrats verlaufen.
3. Bei einem Rechteck lassen sich zwei Symmetrieachsen einzeichnen. Diese verlaufen jeweils durch die Mittelpunkte der gegenüberliegenden Seiten.
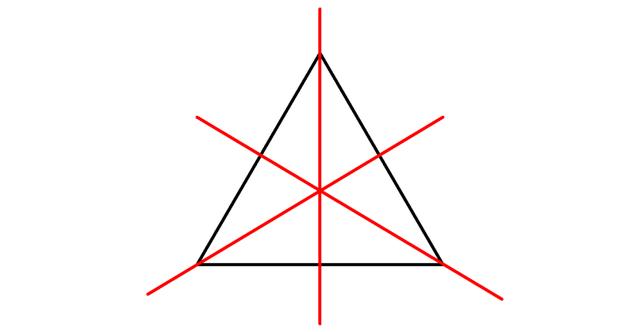
4. Ein gleichseitiges Dreieck hat drei Symmetrieachsen, da es drei gleiche Seiten hat. Diese verlaufen jeweils durch den Mittelpunkt einer Seite und den gegenüberliegenden Eckpunkt.
5. Ein gleichschenkliges Dreieck hat nur eine Spiegelachse, da es zwei gleiche Seiten, aber keine gleichen Winkel hat.
6. Ein Kreis hat unendlich viele Spiegelachsen, da jede Linie durch den Mittelpunkt des Kreises eine Symmetrieachse ist.
Symmetrieachsen sind in vielen Alltagsgegenständen und -formen zu finden. Beispielsweise haben viele Möbelstücke, wie Tische oder Stühle, eine achsensymmetrische Form. Auch in der Natur gibt es zahlreiche Beispiele für Achsensymmetrie, wie zum Beispiel Blütenblätter oder Schneeflocken.
Es ist auch möglich, dass Funktionen achsensymmetrisch sind. Dabei wird die Symmetrie zur y-Achse nachgewiesen, indem man die Funktion mit ihrer negativen Entsprechung vergleicht. Wenn f(x) = f(-x) gilt, ist die Funktion achsensymmetrisch zur y-Achse.
Punktsymmetrie ist ein weiteres Symmetrieverhalten, das bei Figuren und Funktionen auftreten kann. Bei der Punktsymmetrie spiegelt sich die Figur oder Funktion an einem Punkt und erzeugt eine umgedrehte Kopie des Originals.
Das waren einige Erklärungen zur Symmetrieachse und ihren Eigenschaften.
Alles, was du über Symmetrieachsen wissen musst
Was ist eine Symmetrieachse?
Eine Symmetrieachse ist eine Linie, an der eine Figur gespiegelt wird und die beiden Hälften der Figur deckungsgleich sind. Sie wird auch als Spiegelachse bezeichnet. Eine Figur kann mehrere Symmetrieachsen haben, je nach ihrer Form.
Was ist Achsensymmetrie?
Achsensymmetrie wird auch als Spiegelsymmetrie bezeichnet und tritt bei Figuren auf. Eine Figur ist achsensymmetrisch, wenn sie sich an einer Symmetrieachse spiegeln lässt und die gespiegelte Hälfte genau mit der anderen Hälfte übereinstimmt. Ein Beispiel für eine achsensymmetrische Figur ist ein Quadrat, das vier Symmetrieachsen hat.
Wie erkennt man Achsensymmetrie bei Funktionen?
Bei Funktionen wird die Achsensymmetrie zur y-Achse untersucht. Wenn gilt f(x) = f(-x), dann ist die Funktion achsensymmetrisch zur y-Achse. Das bedeutet, dass jeder Punkt auf der Kurve der Funktion bei einer Spiegelung an der y-Achse ebenfalls ein Kurvenpunkt ist.
Was ist Punktsymmetrie?
Punktsymmetrie tritt ebenfalls bei Figuren auf. Dabei wird die Figur an einem Punkt gespiegelt und es entsteht eine umgedrehte Kopie der Originalfigur. Eine punktsymmetrische Funktion spiegelt sich nicht an einer Geraden wie bei der Achsensymmetrie, sondern an einem Punkt. Eine Funktion ist punktsymmetrisch zum Ursprung, wenn gilt -f(x) = f(-x).
Beispiele für achsensymmetrische Figuren
Ein Quadrat hat immer vier Symmetrieachsen. Zwei verlaufen durch die Mitte und zwei durch die Ecken des Quadrates. Bei einem Rechteck lassen sich zwei Symmetrieachsen einzeichnen. Drei Symmetrieachsen sind bei einem gleichseitigen Dreieck zu finden. Ein gleichschenkliges Dreieck hat dagegen nur eine Spiegelachse. Auch ein gleichschenkliges Trapez hat nur eine Spiegelachse. Bei einem Kreis verlaufen die Symmetrieachsen durch den Mittelpunkt und es gibt unendlich viele Spiegelachsen.
Anwendung der Achsensymmetrie im Alltag
Achsensymmetrische Figuren begegnen uns täglich in unserem Alltag. Wenn du dich in deinem Zimmer umsiehst, entdeckst du sicherlich zahlreiche Beispiele für Achsensymmetrie, zum Beispiel an Möbelstücken oder Dekorationen.
Wenn du noch weitere Informationen zum Thema Symmetrieverhalten von Figuren nachlesen möchtest, dann klicke auf den angegebenen Link.
Wie man eine Symmetrieachse bestimmt und nutzt
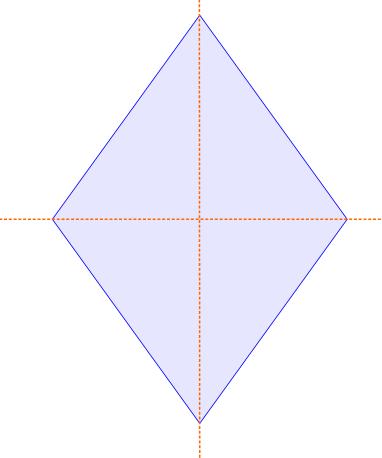
Eine Symmetrieachse ist eine Linie, an der eine Figur gespiegelt wird und die gespiegelte Hälfte genau mit der anderen Hälfte übereinstimmt. Um eine Symmetrieachse zu bestimmen, kann man folgende Schritte befolgen:
1. Betrachte die Figur und suche nach möglichen Spiegelachsen. Bei vielen Figuren wie Quadraten oder Rechtecken sind die Symmetrieachsen leicht zu erkennen, da sie durch die Mitte oder Ecken der Figur verlaufen.
2. Zeichne eine mögliche Symmetrieachse ein und überprüfe, ob die gespiegelte Hälfte genau mit der anderen Hälfte übereinstimmt. Falls dies nicht der Fall ist, versuche eine andere Achse einzufügen.
3. Wenn du unsicher bist, ob deine eingezeichnete Achse tatsächlich eine Symmetrieachse ist, kannst du einen Test machen: Spiegele alle Eckpunkte oder markante Punkte an deiner eingezeichneten Achse und überprüfe, ob sie auf der anderen Seite der Achse liegen.
4. Wenn alle Punkte auf beiden Seiten der Achse übereinstimmen, hast du die richtige Symmetrieachse gefunden.
Eine Symmetrieachse kann verwendet werden, um weitere Eigenschaften einer Figur zu bestimmen oder um das Spiegeln von Figuren zu erleichtern. Durch das Wissen um die Symmetrieachse können wir auch achsensymmetrische Funktionen untersuchen und ihre Eigenschaften bestimmen.
Die Rolle der Symmetrieachse in geometrischen Figuren
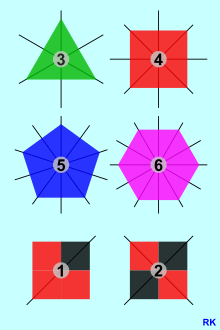
Achsensymmetrie in geometrischen Figuren
Die Achsensymmetrie spielt eine wichtige Rolle in geometrischen Figuren. Eine Figur wird als achsensymmetrisch bezeichnet, wenn sie sich an einer Symmetrieachse spiegeln lässt und die gespiegelte Hälfte genau mit der anderen Hälfte übereinstimmt. Diese Symmetrieachse wird auch als Spiegelachse bezeichnet.
– Ein Quadrat hat immer vier Symmetrieachsen, zwei verlaufen durch die Mitte und zwei durch die Ecken des Quadrates.
– Bei einem Rechteck lassen sich zwei Symmetrieachsen einzeichnen.
– Ein gleichseitiges Dreieck hat drei Symmetrieachsen, während ein gleichschenkliges Dreieck nur eine Spiegelachse besitzt.
– Auch ein gleichschenkliges Trapez hat nur eine Spiegelachse.
– Bei einem Kreis verlaufen die Symmetrieachsen durch den Mittelpunkt. Da ein Kreis unendlich viele Punkte auf der Umfangslinie besitzt, hat er auch unendlich viele Spiegelachsen.
Diese achsensymmetrischen Figuren können wir täglich in unserem Alltag finden. Beispielsweise sind Möbelstücke oder Gebäude oft achsensymmetrisch gestaltet.
Achsensymmetrie bei Funktionen
Auch bei Funktionen spielt die Achsensymmetrie eine wichtige Rolle. Dabei wird die Funktion an der y-Achse gespiegelt. Eine Funktion f(x) ist achsensymmetrisch zur y-Achse, wenn f(x) = f(-x) gilt. Das bedeutet, dass jeder Punkt auf der Funktion bei der Spiegelung an der y-Achse ebenfalls ein Kurvenpunkt ist.
Um die Achsensymmetrie einer Funktion nachzuweisen, kann man die Funktion f(-x) berechnen und mit der ursprünglichen Funktion f(x) vergleichen. Stimmen beide Funktionen überein, ist die Funktion achsensymmetrisch zur y-Achse.
Die Symmetrie zur y-Achse bei Funktionen ist besonders wichtig in der Mathematik und wird häufig verwendet, um bestimmte Eigenschaften von Funktionen zu analysieren und zu beweisen.
Eine Symmetrieachse ist eine imaginäre Linie, die eine Figur in zwei identische Hälften teilt. Sie spielt eine wichtige Rolle in der Geometrie und ermöglicht es uns, Muster und Strukturen zu erkennen. Durch das Verständnis von Symmetrieachsen können wir komplexe Formen analysieren und sie in einfachere Teile zerlegen.

