Eine Dezimalzahl ist eine Zahl, die in unserem Alltag am häufigsten vorkommt. Sie besteht aus Ziffern von 0 bis 9 und einem Dezimaltrennzeichen. Dezimalzahlen ermöglichen präzise Messungen und Berechnungen in verschiedenen Bereichen wie Mathematik, Wirtschaft und Naturwissenschaften. In diesem Artikel werden wir uns genauer mit den Eigenschaften und der Verwendung von Dezimalzahlen befassen.
Was ist eine Dezimalzahl und wie wird sie gerundet?
Eine Dezimalzahl ist eine Zahl, die einen ganzzahligen Anteil und einen dezimalen Anteil hat. Der dezimale Anteil wird durch das Komma oder den Punkt vom ganzzahligen Teil getrennt. Zum Beispiel ist die Zahl 3,14 eine Dezimalzahl, da der ganzzahlige Teil 3 ist und der dezimale Teil 0,14.
Um eine Dezimalzahl zu runden, müssen wir uns auf die Nachkommastelle konzentrieren. Die Nachkommastelle gibt an, wie genau die Zahl ist. Wenn wir eine Dezimalzahl auf- oder abrunden möchten, müssen wir entscheiden, auf welche Stelle wir runden möchten.
Beim Runden einer Dezimalzahl gibt es zwei Möglichkeiten: das Abrunden und das Aufrunden. Beim Abrunden runden wir die Zahl zur nächstkleineren Ganzzahl. Zum Beispiel wird die Zahl 3,14 auf 3 abgerundet. Beim Aufrunden runden wir die Zahl zur nächsthöheren Ganzzahl. In diesem Fall würde die Zahl 3,14 auf 4 aufgerundet werden.
Um zu entscheiden, ob wir eine Dezimalzahl aufrunden oder abrunden sollen, betrachten wir die erste Ziffer nach der gewünschten Rundungsstelle. Ist diese Ziffer kleiner als 5, runden wir ab; ist sie größer oder gleich 5, runden wir auf.
Es ist auch wichtig zu beachten, dass beim Runden von Dezimalzahlen immer ein Verlust an Genauigkeit auftritt. Das bedeutet, dass das gerundete Ergebnis nicht mehr so präzise ist wie die ursprüngliche Zahl. Daher ist es wichtig, die Anzahl der Nachkommastellen zu berücksichtigen und das gerundete Ergebnis entsprechend anzugeben.
Zusammenfassend lässt sich sagen, dass Dezimalzahlen Zahlen mit einem dezimalen Anteil sind, der durch das Komma oder den Punkt vom ganzzahligen Teil getrennt wird. Beim Runden einer Dezimalzahl müssen wir entscheiden, ob wir sie aufrunden oder abrunden möchten, basierend auf der ersten Ziffer nach der gewünschten Rundungsstelle. Es ist auch wichtig zu beachten, dass beim Runden immer ein Verlust an Genauigkeit auftritt.
Die Bedeutung von Dezimalzahlen und wie man sie ordnet.
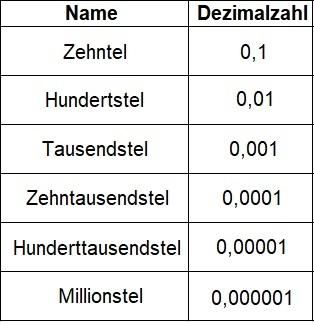
1. Die Bedeutung von Dezimalzahlen
Dezimalzahlen sind Zahlen, die eine Nachkommastelle haben und somit genauer als ganze Zahlen sind. Sie werden verwendet, um Messungen oder Werte darzustellen, die nicht immer ganzzahlig sind. Zum Beispiel können Gewichte, Längen oder Geldbeträge in Dezimalzahlen angegeben werden. Dezimalzahlen ermöglichen es uns, präzisere Informationen zu erhalten.
2. Das Ordnen von Dezimalzahlen
Um Dezimalzahlen zu ordnen, betrachten wir zunächst die Stellen vor dem Komma. Je größer der Wert dieser Stellen ist, desto größer ist auch die Zahl insgesamt. Wenn zwei Dezimalzahlen den gleichen Wert vor dem Komma haben, vergleichen wir die erste Nachkommastelle. Ist diese gleich, schauen wir uns die zweite Nachkommastelle an und so weiter.
Beispiel:
– 0,25
– 0,35
– 0,15
Wir vergleichen zuerst den Wert vor dem Komma: Alle drei Zahlen haben eine Null davor.
Dann vergleichen wir die erste Nachkommastelle: 0,25 < 0,35 < 0,15.
Die geordnete Reihenfolge wäre also: 0,15 – 0,25 – 0,35.
Es ist wichtig zu beachten, dass bei der Reihenfolge von Dezimalzahlen auch negative Zahlen berücksichtigt werden können. In diesem Fall wird das Minuszeichen vor der Zahl berücksichtigt und die gleichen Regeln für das Ordnen gelten.
3. Das Runden von Dezimalzahlen
Beim Runden von Dezimalzahlen geht es darum, eine Zahl auf eine bestimmte Anzahl von Nachkommastellen zu reduzieren. Dies kann hilfreich sein, um genaue Ergebnisse in praktischere oder verständlichere Formate zu bringen.
Es gibt verschiedene Rundungsregeln, aber die gebräuchlichste Methode ist das sogenannte „kaufmännische Runden“. Dabei wird die betrachtete Nachkommastelle um eins erhöht und alle weiteren Nachkommastellen werden abgeschnitten.
Beispiel:
– 2,3456 gerundet auf zwei Nachkommastellen: 2,35
– 7,8129 gerundet auf drei Nachkommastellen: 7,813
Es ist wichtig zu beachten, dass beim Runden auch auf die nächstgelegene ganze Zahl gerundet werden kann. In diesem Fall wird die betrachtete Nachkommastelle um eins erhöht und alle weiteren Nachkommastellen werden auf Null gesetzt.
Beispiel:
– 4,6 gerundet auf die nächstgelegene ganze Zahl: 5
– 8,4 gerundet auf die nächstgelegene ganze Zahl: 8
Das Runden von Dezimalzahlen ermöglicht es uns also, Zahlen übersichtlicher darzustellen und sie an unsere Bedürfnisse anzupassen.
Runden und Ordnen von Dezimalzahlen: Wichtige Aspekte im Umgang mit Zahlen.
1. Runden von Dezimalzahlen
Beim Runden von Dezimalzahlen gibt es verschiedene Verfahren, je nachdem auf welche Stelle gerundet werden soll. Die gängigsten Verfahren sind das Aufrunden und das Abrunden. Beim Aufrunden wird die Zahl zur nächsten größeren Zahl gerundet, während beim Abrunden zur nächsten kleineren Zahl gerundet wird. Dabei ist zu beachten, dass bei einer 5 als Nachkommastelle immer auf- oder abgerundet wird, je nachdem ob die vorhergehende Ziffer gerade oder ungerade ist.
2. Ordnen von Dezimalzahlen
Um Dezimalzahlen zu ordnen, werden sie in der Regel auf dem Zahlenstrahl dargestellt. Dabei werden die Zahlen entsprechend ihrer Größe angeordnet. Es ist wichtig, die Position der Nachkommastelle zu berücksichtigen, da dies den Wert der Zahl beeinflusst. Bei gleicher Vorkommastelle entscheidet die Größe der Nachkommastellen über die Reihenfolge.
3. Genauigkeit und Signifikanz
Bei der Angabe von Ergebnissen oder Messwerten ist es oft nicht notwendig oder möglich, eine unbegrenzte Anzahl an Nachkommastellen anzugeben. Stattdessen wird eine bestimmte Genauigkeit festgelegt, zum Beispiel zwei Nachkommastellen für Centbeträge. Es ist wichtig zu verstehen, dass durch Rundungen oder Begrenzung der Anzahl an Nachkommastellen eine gewisse Ungenauigkeit entstehen kann. Daher sollte die Anzahl der angegebenen Nachkommastellen immer im Kontext betrachtet werden.
4. Rechnen mit Dezimalzahlen
Um mit Dezimalzahlen zu rechnen, müssen die Grundoperationen Addition, Subtraktion, Multiplikation und Division beherrscht werden. Dabei ist es wichtig, die Stellenschreibweise zu beachten und die Zahlen entsprechend auszurichten. Beim Multiplizieren und Dividieren können auch geschätzte Werte verwendet werden, um das Ergebnis zu überprüfen oder einen schnelleren Lösungsweg zu finden.
5. Besonderheiten bei irrationalen Zahlen
Irrationale Zahlen sind nicht abbrechende und nicht periodische Dezimalzahlen wie zum Beispiel die Zahl π. Da sie sich nicht als Bruch darstellen lassen, müssen sie in ihrer Dezimalschreibweise verwendet werden. Es ist wichtig zu verstehen, dass irrationale Zahlen eine unendliche Anzahl an Nachkommastellen haben und daher bei Berechnungen oft gerundet oder auf eine bestimmte Genauigkeit begrenzt werden müssen.
Diese Aspekte sind beim Runden und Ordnen von Dezimalzahlen zu beachten, um korrekte Ergebnisse zu erzielen und ein besseres Verständnis für den Umgang mit Zahlen zu entwickeln.
Wie funktioniert das Runden und Ordnen von Dezimalzahlen?
Runden von Dezimalzahlen
Beim Runden von Dezimalzahlen geht es darum, eine Zahl auf eine bestimmte Anzahl von Nachkommastellen zu reduzieren. Dies kann zum Beispiel sinnvoll sein, wenn man Geldbeträge auf Centbeträge genau angeben möchte. Beim Runden einer Zahl wird die nächste Nachkommastelle betrachtet und je nach Wert dieser Stelle wird die Zahl entsprechend auf- oder abgerundet. Wenn die nächste Nachkommastelle kleiner als 5 ist, wird abgerundet, ansonsten wird aufgerundet.
Ordnen von Dezimalzahlen
Beim Ordnen von Dezimalzahlen geht es darum, Zahlen in einer bestimmten Reihenfolge zu sortieren. Dabei werden die Zahlen nach ihrer Größe geordnet. Die einfachste Methode ist es, die Zahlen auf einem Zahlenstrahl einzuzeichnen und sie dort zu vergleichen. Man kann aber auch die Stellenschreibweise verwenden, um die Zahlen zu ordnen. Dabei werden die Zahlen so geschrieben, dass sie jeweils gleich viele Nachkommastellen haben und dann nach der Anzahl der Vorkommastellen geordnet.
Zusammenfassend ist beim Runden und Ordnen von Dezimalzahlen wichtig, dass man weiß, wie man die richtige Anzahl von Nachkommastellen auswählt und wie man die Zahlen entsprechend ordnet. Durch das Runden und Ordnen können wir unsere Ergebnisse übersichtlicher darstellen und besser vergleichen.
Dezimalzahlen: Rundungsregeln und Ordnung auf dem Zahlenstrahl.
Rundungsregeln für Dezimalzahlen:
– Beim Runden von Dezimalzahlen gibt es bestimmte Regeln zu beachten. Die erste Regel besagt, dass bei einer Nachkommastelle von 5 oder größer aufgerundet wird. Ist die Nachkommastelle kleiner als 5, wird abgerundet.
– Wenn die Nachkommastelle genau 5 ist, wird aufgerundet, wenn die Vorgängerziffer ungerade ist, und abgerundet, wenn sie gerade ist.
– Bei mehreren Nachkommastellen gilt das gleiche Prinzip: Die letzte zu rundende Stelle bestimmt das Ergebnis.
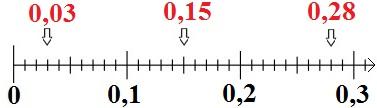
Ordnung von Dezimalzahlen auf dem Zahlenstrahl:
– Um Dezimalzahlen ordnen zu können, nutzen wir den Zahlenstrahl. Dabei werden die Zahlen entsprechend ihrer Größe auf dem Strahl angeordnet.
– Eine größere Dezimalzahl liegt weiter rechts auf dem Zahlenstrahl als eine kleinere Dezimalzahl.
– Wenn zwei Dezimalzahlen gleich viele Vorkommastellen haben, vergleichen wir die erste unterschiedliche Nachkommastelle. Die Zahl mit der größeren ersten unterschiedlichen Nachkommastelle ist größer.
Beispiel:
Angenommen wir haben die Dezimalzahlen 1,234; 1,239; 1,24; und 1,23. Auf dem Zahlenstrahl würden sie wie folgt angeordnet werden:
1,23 – 1,234 – 1,24 – 1,239
Das Runden und Ordnen von Dezimalzahlen ist wichtig, um genaue Ergebnisse zu erhalten und die Zahlen nach ihrer Größe einzuteilen.
Der Umgang mit Dezimalzahlen: Runden und Ordnen leicht gemacht.
Runden von Dezimalzahlen
Beim Runden von Dezimalzahlen ist es wichtig, die gewünschte Genauigkeit zu beachten. Möchtest du beispielsweise eine Dezimalzahl auf zwei Nachkommastellen runden, schaust du dir die dritte Nachkommastelle an. Ist diese kleiner als 5, rundest du ab, ist sie größer oder gleich 5, rundest du auf. Das bedeutet, dass die zweite Nachkommastelle um eins erhöht wird. Die weiteren Nachkommastellen werden einfach gestrichen.
Beispiel:
Die Zahl 3,14159 soll auf zwei Nachkommastellen gerundet werden.
Die dritte Nachkommastelle ist eine 1, also wird abgerundet.
Das Ergebnis lautet 3,14.
Ordnen von Dezimalzahlen
Um Dezimalzahlen zu ordnen, betrachtest du zunächst die Ziffern vor dem Komma. Je größer diese sind, desto größer ist auch die Dezimalzahl. Wenn die Ziffern vor dem Komma gleich sind, schaust du dir die erste nicht-übereinstimmende Ziffer nach dem Komma an. Ist diese kleiner bei einer Zahl als bei der anderen, so ist auch die Zahl kleiner.
Beispiel:
Du möchtest die Dezimalzahlen 0,75; 0,8 und 0,7 in aufsteigender Reihenfolge ordnen.
Die Ziffern vor dem Komma sind alle gleich (0), also betrachtest du die erste nicht-übereinstimmende Ziffer nach dem Komma.
Die erste Ziffer bei 0,75 ist eine 7, bei 0,8 ist sie eine 8 und bei 0,7 ist sie eine 7.
Da die Ziffern bei 0,75 und 0,7 gleich sind, schaust du auf die nächste nicht-übereinstimmende Ziffer.
Die zweite Ziffer bei 0,75 ist eine 5 und bei 0,7 ist sie eine 0.
Daher lautet die aufsteigende Reihenfolge: 0,7; 0,75; 0,8.
Zusammenfassung
Beim Runden von Dezimalzahlen musst du die gewünschte Genauigkeit beachten. Je nachdem ob die nächste Nachkommastelle kleiner oder größer/gleich als fünf ist, rundest du ab oder auf. Beim Ordnen von Dezimalzahlen betrachtest du zunächst die Ziffern vor dem Komma. Sind diese gleich, schaust du dir die erste nicht-übereinstimmende Ziffer nach dem Komma an.
Zusammenfassend kann gesagt werden, dass Dezimalzahlen eine wichtige Darstellungsform von Zahlen sind, bei der sie in Basis 10 dargestellt werden. Sie bestehen aus einer ganzzahligen Zahl und einem Bruchteil, der durch einen Dezimalpunkt getrennt ist. Dezimalzahlen finden in vielen Bereichen Anwendung, wie zum Beispiel in der Mathematik, Finanzwesen und Naturwissenschaften. Ein Verständnis für Dezimalzahlen ist daher grundlegend für das Lösen von mathematischen Aufgaben und den Umgang mit dezimalen Größen im Alltag.