Was ist eine Dezimalzahl? Grundlagen, Arten und Eigenschaften

Eine Dezimalzahl ist eine Zahl, die im Zehnersystem dargestellt wird und sowohl Ganzzahlen als auch Bruchteile darstellen kann. Sie setzt sich aus einer ganzen Zahl und einem dezimalen Teil zusammen, der durch ein Komma oder einen Punkt abgetrennt wird. Dezimalzahlen sind in unserem Alltag weit verbreitet und werden für verschiedene Berechnungen und Messungen verwendet. In diesem Artikel erfährst du mehr über die Eigenschaften und Verwendung von Dezimalzahlen.

Definition und Eigenschaften von Dezimalzahlen

Definition

Dezimalzahlen sind grundsätzlich alle Zahlen, die im Stellensystem mit der Basis 10 (Dezimalsystem) aufgeschrieben werden. Das bedeutet, dass sie für die meisten in der Schule und im Alltag verwendeten Zahlen gelten. Beispiele für Dezimalzahlen sind -1,5, 2 und 3,141.592.653.589.793…

Verwendung in Schulbüchern

In vielen Schulbüchern wird der Begriff „Dezimalzahlen“ jedoch enger verwendet und bezieht sich häufig nur auf Kommazahlen. Genauer gesagt handelt es sich um Dezimalzahlen, die mindestens eine Stelle hinter dem Komma haben, die nicht null ist.

Arten von Dezimalzahlen

Es gibt drei Arten von Dezimalzahlen:

1. Abbrechende Dezimalzahlen: Diese haben nur endlich viele Nachkommastellen, die nicht null sind oder ab einer bestimmten Stelle nur noch Nullen aufweisen. Sie entsprechen den Dezimalbrüchen, also Brüchen mit einer Zehnerpotenz im Nenner.

Beispiel: Die Zahl 7/20 kann als dezimale Darstellung geschrieben werden als 0,35.

2. Periodische Dezimalzahlen: Bei diesen wiederholt sich ab einer bestimmten Stelle hinter dem Komma eine Ziffer oder Ziffernfolge immer weiter bis ins Unendliche. Diese Perioden werden mit einem Überstrich notiert.

Beispiel: Die Zahl 7/6 kann als dezimale Darstellung geschrieben werden als 1,166…

3. Irrationale Zahlen: Diese entsprechen Dezimalzahlen, die weder abbrechen noch eine Periode zeigen. Solche nicht abbrechenden und nicht periodischen Dezimalzahlen können nur angenähert aufgeschrieben werden. Eine exakte Darstellung ist nur durch Symbole wie „e“, „π“ oder „√2“ möglich.

Betrag einer Zahl

Der Betrag einer Zahl gibt den Abstand der Zahl vom Nullpunkt auf der Zahlengeraden an. Er wird auch als absolute Betrag bezeichnet und ist immer eine positive Zahl.

Beispiel: Der Betrag von -5 ist 5 und der Betrag von 8 ist ebenfalls 8.

Es gibt verschiedene Möglichkeiten, den Betrag einer Zahl zu berechnen. Eine gebräuchliche Schreibweise ist |x| für den Betrag der Zahl x.

Zusammenfassend sind Dezimalzahlen Zahlen im Dezimalsystem mit der Basis 10. Sie können abbrechend, periodisch oder irrational sein. Der Betrag einer Zahl gibt den Abstand zur Null auf der Zahlengeraden an und ist immer positiv.

Arten von Dezimalzahlen: Abbrechend, periodisch und irrational

Arten von Dezimalzahlen: Abbrechend, periodisch und irrational

Dezimalzahlen können in verschiedene Arten unterteilt werden, je nachdem ob sie abbrechen, periodisch sind oder irrational.

Abbrechende Dezimalzahlen haben nur endlich viele Nachkommastellen, die nicht null sind. Sie entsprechen den Dezimalbrüchen, also den Brüchen mit einer Zehnerpotenz im Nenner. Ein Beispiel für eine abbrechende Dezimalzahl ist \(0{,}35\), was dem Bruch \(\frac {7}{20}\) entspricht.

Periodische Dezimalzahlen wiederholen sich ab einer bestimmten Stelle hinter dem Komma immer weiter bis ins Unendliche. Diese Wiederholung wird mit einem Überstrich notiert. Ein Beispiel für eine periodische Dezimalzahl ist \(1{,}1\bar6\), was dem Bruch \(\frac {7}{6}\) entspricht.

Abbrechende und periodische Dezimalzahlen sind rationale Zahlen, da sie als Verhältnis zweier ganzer Zahlen dargestellt werden können.

Irrationale Zahlen hingegen entsprechen Dezimalzahlen, die weder abbrechen noch jemals eine Periode zeigen. Solche nicht abbrechenden und nicht periodischen Dezimalzahlen lassen sich immer nur angenähert aufschreiben und exakt ist nur die Angabe eines Symbols wie „\(e\)“, „\(\pi\)“ oder „\(\sqrt 2\)“. Irrationale Zahlen können nicht als Verhältnis zweier ganzer Zahlen dargestellt werden.

Mathematisch genau müsste man solche Dezimalzahlen als Grenzwert einer Folge von abbrechenden oder periodischen Dezimalzahlen definieren.

Einige Mathematikbücher vermeiden den Ausdruck Dezimalzahlen und sprechen stattdessen von Dezimalbrüchen, allerdings fallen darunter nur diejenigen Dezimalzahlen, die nicht periodisch sind.

Unterschied zwischen Dezimalzahlen und Dezimalbrüchen

Der Unterschied zwischen Dezimalzahlen und Dezimalbrüchen liegt in ihrer Darstellung und ihrem Wertebereich.

Dezimalzahlen sind grundsätzlich alle Zahlen, die im Stellensystem mit der Basis 10 (Dezimalsystem) aufgeschrieben werden. Dies umfasst Zahlen wie -1,5, 2 oder 3,141592653589793… Dezimalzahlen können sowohl vor dem Komma als auch nach dem Komma beliebig viele Stellen haben.

Dezimalbrüche sind eine spezielle Art von Dezimalzahlen. Sie sind Bruchzahlen, bei denen der Nenner eine Zehnerpotenz ist. Das bedeutet, dass sie in Zifferndarstellung mindestens eine Stelle hinter dem Komma haben müssen, die nicht null ist. Es gibt drei Arten von Dezimalbrüchen: abbrechende Dezimalbrüche, periodische Dezimalbrüche und nicht abbrechende und nicht periodische Dezimalbrüche.

Abbrechende Dezimalbrüche haben nur endlich viele Nachkommastellen, die nicht null sind. Sie können als Bruchzahl mit einer Zehnerpotenz im Nenner dargestellt werden. Ein Beispiel dafür ist 7/20 = 0,35.

Periodische Dezimalbrüche wiederholen sich ab einer bestimmten Stelle hinter dem Komma immer weiter bis ins Unendliche. Sie werden mit einem Überstrich über der wiederholten Ziffer oder Ziffernfolge notiert. Ein Beispiel dafür ist 7/6 = 1,166…

Nicht abbrechende und nicht periodische Dezimalbrüche sind irrational und können nicht exakt dargestellt werden. Sie lassen sich nur angenähert aufschreiben. Einige Beispiele dafür sind die Zahl e, die Kreiszahl Pi oder die Quadratwurzel von 2.

In einigen Mathematikbüchern wird der Begriff Dezimalzahlen vermieden und stattdessen von Dezimalbrüchen gesprochen. Dabei fallen jedoch nur diejenigen Dezimalzahlen darunter, die nicht periodisch sind. Abbrechende Dezimalbrüche werden also als Dezimalbrüche bezeichnet, während periodische und nicht abbrechende Dezimalbrüche als irrationale Zahlen bezeichnet werden.

Der Betrag einer Zahl ist der Abstand dieser Zahl von der Null auf der Zahlengeraden. Er gibt an, wie weit eine Zahl vom Nullpunkt entfernt ist, unabhängig davon, ob sie positiv oder negativ ist. Der Betrag einer positiven Zahl entspricht einfach der Zahl selbst. Der Betrag einer negativen Zahl ergibt sich durch das Vorzeichenwechseln zu einer positiven Zahl mit dem gleichen Absolutwert. Der Betrag einer Zahl wird oft mit den absoluten Wertstrichen um die Zahl herum dargestellt (z.B. |x|).

Präzise Darstellung von nicht abbrechenden und nicht periodischen Dezimalzahlen

Die präzise Darstellung von nicht abbrechenden und nicht periodischen Dezimalzahlen ist eine Herausforderung in der Mathematik. Solche Zahlen können nicht exakt aufgeschrieben werden, sondern nur approximiert. Eine Möglichkeit, diese Zahlen darzustellen, ist die Verwendung eines Symbols wie „e“, „π“ oder „√2“. Diese Symbole repräsentieren bestimmte irrationale Zahlen, die keine endliche oder sich wiederholende Dezimaldarstellung haben.

Eine andere Methode zur Darstellung solcher Dezimalzahlen besteht darin, sie als Grenzwert einer Folge von abbrechenden oder periodischen Dezimalzahlen zu definieren. Dies bedeutet, dass man eine Folge von Dezimalzahlen betrachtet, die immer näher an die gesuchte Zahl herankommen. Die Genauigkeit der Approximation kann beliebig erhöht werden, indem man mehr Nachkommastellen berücksichtigt.

Es ist wichtig zu beachten, dass nicht abbrechende und nicht periodische Dezimalzahlen irrational sind und daher unendlich viele Nachkommastellen haben. Ihre genaue Darstellung ist daher unmöglich. Die Verwendung von Symbolen oder Grenzwerten ermöglicht es jedoch, diese Zahlen mathematisch korrekt zu beschreiben.

In einigen Mathematikbüchern wird der Begriff „Dezimalbrüche“ anstelle von „Dezimalzahlen“ verwendet, um genau auf diese Art von Zahlen hinzuweisen – Dezimalbrüche, die weder abbrechen noch periodisch sind.

Zusammenfassend lässt sich sagen, dass nicht abbrechende und nicht periodische Dezimalzahlen präzise nur durch Symbole oder als Grenzwert einer Folge von approximierenden Dezimalzahlen dargestellt werden können. Ihre genaue Darstellung ist mathematisch anspruchsvoll, aber durch diese Methoden möglich.

Bedeutung des Betrags einer Zahl in der Mathematik

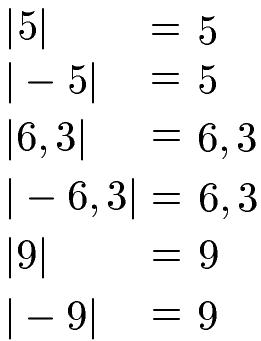
Der Betrag einer Zahl ist ein mathematischer Ausdruck, der angibt, wie weit eine Zahl von der Null entfernt ist. Er wird durch das Symbol „|“ um die Zahl herum dargestellt. Der Betrag einer positiven Zahl entspricht einfach der Zahl selbst, da sie bereits einen Abstand von null hat. Zum Beispiel ist der Betrag von 5 gleich 5.

Für negative Zahlen wird der Betrag verwendet, um den positiven Wert der Zahl darzustellen. Der Betrag einer negativen Zahl ergibt sich also aus dem Vorzeichenwechsel und entspricht dem positiven Wert der Zahl. Zum Beispiel ist der Betrag von -7 gleich 7.

Der Betrag einer Zahl kann auch als Distanz zwischen dieser Zahl und null interpretiert werden. Es spielt keine Rolle, ob die gegebene Zahl positiv oder negativ ist, da beide den gleichen Abstand von null haben. Daher ist der Betrag immer eine positive oder nicht-negative Zahl.

In mathematischen Gleichungen kann der Betrag verwendet werden, um Ungleichungen zu formulieren oder um Bedingungen für bestimmte Bereiche festzulegen. Zum Beispiel könnte man sagen: „Der Betrag von x muss kleiner als 10 sein“, was bedeutet, dass x entweder positiv oder negativ sein kann, aber sein absoluter Wert darf nicht größer als 10 sein.

Der Betrag einer komplexen Zahl in der Mathematik wird durch die Quadratwurzel aus der Summe ihrer quadrierten Real- und Imaginärteile berechnet. Dies ermöglicht es uns, den Abstand zwischen dem Ursprung (Nullpunkt) und dem Punkt in der komplexen Ebene zu bestimmen, an dem sich die komplexe Zahl befindet.

In der Geometrie kann der Betrag einer Zahl als Länge eines Vektors interpretiert werden. Der Betrag eines Vektors gibt an, wie weit er von seinem Ursprung entfernt ist und wird durch die Wurzel aus der Summe seiner quadrierten Komponenten berechnet.

Zusammenfassend lässt sich sagen, dass der Betrag einer Zahl in der Mathematik verwendet wird, um den Abstand dieser Zahl von null darzustellen oder um Bedingungen für bestimmte Bereiche festzulegen. Er kann sowohl für reale Zahlen als auch für komplexe Zahlen und Vektoren berechnet werden.

Anwendungsbereiche von Dezimalzahlen im Alltag und in der Schule

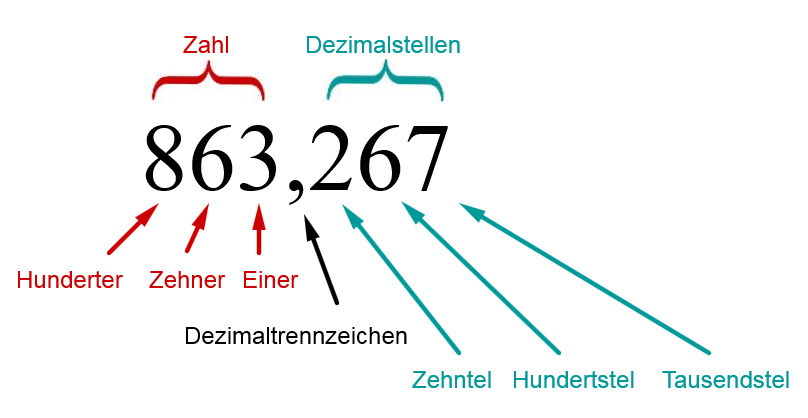
Die Anwendungsbereiche von Dezimalzahlen im Alltag und in der Schule sind vielfältig. Hier sind einige Beispiele:

1. Geld: Dezimalzahlen werden im täglichen Umgang mit Geld verwendet, um Beträge genau darzustellen. Zum Beispiel werden Preise in Geschäften oder Online-Shops oft mit Dezimalzahlen angegeben.

2. Maßeinheiten: Dezimalzahlen werden verwendet, um Längen, Gewichte und andere Maßeinheiten genau zu messen und zu berechnen. Zum Beispiel wird die Länge eines Objekts in Metern mit Dezimalstellen angegeben.

3. Noten: In der Schule werden Dezimalzahlen häufig verwendet, um Noten auszudrücken. Eine Note wie 1,5 zeigt an, dass ein Schüler zwischen einer Eins und einer Zwei liegt.

4. Statistik: Bei der Auswertung von Daten und der Erstellung von Diagrammen werden Dezimalzahlen verwendet, um genaue Prozentsätze oder Verhältnisse darzustellen.

5. Wissenschaftliche Berechnungen: In naturwissenschaftlichen Fächern wie Physik oder Chemie werden Dezimalzahlen verwendet, um genaue Messergebnisse oder Berechnungen darzustellen.

6. Finanzmathematik: Bei der Berechnung von Zinsen, Krediten oder Investitionen werden Dezimalzahlen verwendet, um genaue Ergebnisse zu erzielen.

7. Zeit: Bei der Darstellung von Uhrzeiten können Dezimalstellen verwendet werden, um Minuten und Sekunden genau anzugeben.

8. Kochrezepte: In Kochrezepten werden oft Mengenangaben mit Dezimalstellen verwendet, um die genaue Menge einer Zutat anzugeben.

9. Sport: In einigen Sportarten wie Leichtathletik oder Schwimmen werden Dezimalzahlen verwendet, um genaue Zeiten oder Weiten zu messen und zu vergleichen.

10. Wettervorhersage: Bei der Vorhersage von Temperaturen oder Niederschlagsmengen werden Dezimalzahlen verwendet, um genaue Angaben zu machen.

Diese Anwendungsbereiche zeigen, dass Dezimalzahlen im Alltag und in der Schule eine wichtige Rolle spielen, um genaue Messungen, Berechnungen und Darstellungen zu ermöglichen.

Zusammenfassend lässt sich sagen, dass eine Dezimalzahl eine Zahl ist, die einen ganzzahligen Teil und einen dezimalen Teil hat. Der dezimale Teil wird durch den Dezimalpunkt von der ganzen Zahl getrennt. Dezimalzahlen werden in vielen Bereichen verwendet, insbesondere in Mathematik und Finanzwesen, um Genauigkeit und Präzision zu ermöglichen.