Alles über Punktsymmetrie: Figur und Funktion erkennen (90 characters)

Punktsymmetrie bezieht sich auf die Eigenschaft eines Objekts, eine Achse zu haben, entlang der es symmetrisch ist. Aber was bedeutet es wirklich, punktsymmetrisch zu sein? In diesem Artikel werden wir diese Frage untersuchen und die Konzepte hinter der Punktsymmetrie erklären. Lassen Sie uns gemeinsam in die Welt der Symmetrie eintauchen und herausfinden, was es bedeutet, punktsymmetrisch zu sein.

Punktsymmetrie: Was bedeutet das und wie erkennt man sie bei Figuren und Funktionen?

Was ist Punktsymmetrie?

Punktsymmetrie bezieht sich auf die Eigenschaft einer Figur oder Funktion, dass sie um einen bestimmten Punkt gedreht werden kann, ohne ihr Aussehen zu verändern. Dieser Punkt wird als Spiegelzentrum oder Spiegelpunkt bezeichnet. Daher der Name Punktsymmetrie.

Wie erkennt man Punktsymmetrie bei Figuren?

Um zu überprüfen, ob eine Figur punktsymmetrisch ist, kannst du sie um 180° drehen. Wenn sich die Figur dabei nicht verändert und deckungsgleich bleibt, ist sie punktsymmetrisch um das Symmetriezentrum. Beispiele für punktsymmetrische Figuren sind das Quadrat, das Parallelogramm und der Kreis.

Wie erkennt man Punktsymmetrie bei Funktionen?

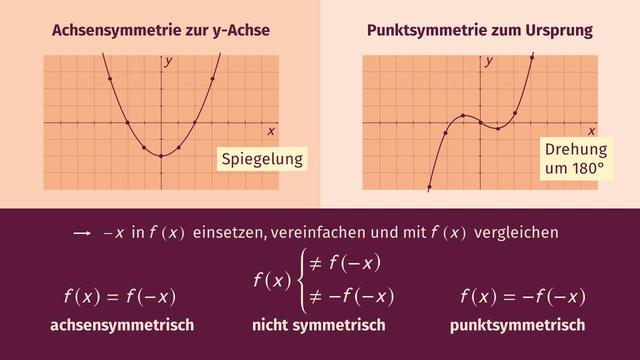
Bei Funktionen kannst du überprüfen, ob sie punktsymmetrisch zum Ursprung sind. Dazu gibt es eine Punktsymmetrie-Formel: Wenn gilt f(-x) = -f(x), ist die Funktion punktsymmetrisch zum Ursprung. Du kannst dies überprüfen, indem du die Funktion für x durch -x ersetzt (f(-x)) und diese mit dem negativen Wert der Funktion (-f(x)) vergleichst. Wenn beide Gleichungen dasselbe Ergebnis liefern, ist die Funktion punktsymmetrisch zum Ursprung.

Punktsymmetrie: Definition, Beispiele und Erkennungsmethoden

Definition:

Die Punktsymmetrie einer Figur oder Funktion bedeutet, dass diese um einen bestimmten Punkt gedreht werden kann, ohne ihr Aussehen zu verändern. Dieser Punkt wird auch als Spiegelzentrum oder Spiegelpunkt bezeichnet. Bei einer Funktion bedeutet Punktsymmetrie, dass die Funktionswerte für x und -x gleich sind.

Beispiele:

– Ein Quadrat ist punktsymmetrisch um sein Symmetriezentrum. Wenn man es um 180° dreht, ändert sich nichts an seiner Form.
– Ein Parallelogramm ist ebenfalls punktsymmetrisch. Es handelt sich dabei um ein „verschobenes“ Rechteck.
– Ein Kreis ist punktsymmetrisch zu seinem Mittelpunkt. Egal wie man ihn dreht, er bleibt immer gleich.

Erkennungsmethoden:

Um herauszufinden, ob eine Funktion punktsymmetrisch zum Ursprung ist, gibt es eine einfache Methode:
1. Berechne f(-x) indem du in der Funktion alle x durch -x ersetzt.
2. Berechne -f(x), indem du ein Minus vor die Funktion schreibst.
3. Vergleiche f(-x) mit -f(x). Wenn beide Gleichungen das gleiche Ergebnis haben, ist die Funktion punktsymmetrisch zum Ursprung.

Es gibt auch noch die Achsensymmetrie, bei der entlang einer bestimmten Achse gespiegelt wird. Es kann hilfreich sein, beide Symmetrien zu kennen und unterscheiden zu können.

Die Bedeutung von Punktsymmetrie bei Figuren und Funktionen verstehen

Was ist Punktsymmetrie?

Punktsymmetrie bezieht sich auf die Eigenschaft einer Figur oder Funktion, dass sie um einen bestimmten Punkt gedreht werden kann, ohne ihr Aussehen zu verändern. Dieser Punkt wird als Spiegelzentrum oder Spiegelpunkt bezeichnet. Wenn eine Figur um 180° gedreht wird, erscheint sie genau so wie vor der Drehung, nur auf dem Kopf stehend. Diese Art der Symmetrie wird als Punktsymmetrie bezeichnet.

Beispiele für punktsymmetrische Figuren

– Ein Quadrat ist ein klassisches Beispiel für eine punktsymmetrische Figur. Wenn man es um 180° dreht, bleibt es unverändert.
– Ein Parallelogramm weist ebenfalls Punktsymmetrie auf. Es ähnelt einem verschobenen Rechteck und behält sein Aussehen bei einer 180°-Drehung.
– Auch ein Kreis ist punktsymmetrisch zu seinem Mittelpunkt. Egal wie man ihn dreht, er sieht immer gleich aus.

Punktsymmetrie bei Funktionen

Auch Funktionen können punktsymmetrisch sein. Um dies zu überprüfen, gibt es eine spezielle Formel: Eine Funktion f ist punktsymmetrisch zum Ursprung, wenn gilt f(-x) = -f(x).

Für die Überprüfung einer Funktion auf Punktsymmetrie zum Ursprung geht man folgendermaßen vor:
1. Berechne f(-x), indem du in der Funktion alle x durch -x ersetzt.
2. Berechne -f(x), indem du ein Minuszeichen vor die Funktion setzt.
3. Vergleiche die beiden Funktionen. Wenn sie gleich sind, erfüllt die Funktion die Punktsymmetrie Formel und ist punktsymmetrisch zum Ursprung.

Es gibt jedoch auch Funktionen, die nicht punktsymmetrisch zum Ursprung sind. In diesem Fall sind f(-x) und -f(x) nicht gleich.

Die Punktsymmetrie ist eine wichtige Eigenschaft bei Figuren und Funktionen, da sie auf eine spezielle Art von Symmetrie hinweist. Sie kann sowohl visuell bei geometrischen Figuren als auch mathematisch bei Funktionen erkannt werden.

Wie erkennt man Punktsymmetrie bei Figuren und Funktionen?

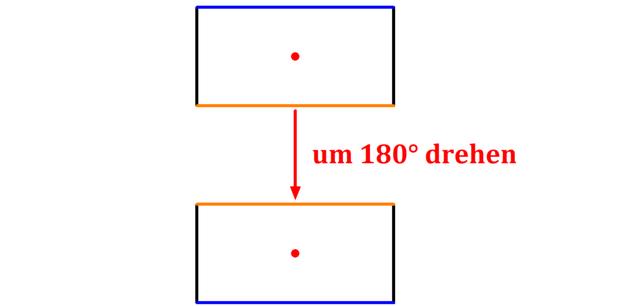
Punktsymmetrie bei Figuren:

– Eine Figur ist punktsymmetrisch, wenn sie um 180° gedreht werden kann, ohne dass sich ihr Aussehen verändert.
– Bei einer 180°-Drehung wird die Figur einfach auf den Kopf gestellt.
– Die Figur wird um ein Spiegelzentrum oder einen Spiegelpunkt gedreht, weshalb sie auch Punktsymmetrie genannt wird.

Beispiele für punktsymmetrische Figuren sind:
– Quadrat: Ein Quadrat bleibt deckungsgleich und punktsymmetrisch um das Symmetriezentrum, wenn es um 180° gedreht wird.
– Parallelogramm: Ein Parallelogramm ist eine Art „verschobenes“ Rechteck und weist ebenfalls Punktsymmetrie auf.
– Kreis: Ein Kreis ist punktsymmetrisch zu seinem Mittelpunkt.

Punktsymmetrie bei Funktionen:

– Auch Funktionen können punktsymmetrisch zum Ursprung sein.
– Um zu überprüfen, ob eine Funktion f punktsymmetrisch zum Ursprung ist, gibt es eine Punktsymmetrie Formel.
– Diese lautet: f(-x) = -f(x).
– Um die Formel anzuwenden, gehst du folgendermaßen vor:
1. Berechne f(-x), indem du alle x in der Funktion mit -x substituierst (denke daran: Minus mal Minus ergibt Plus!).
2. Berechne -f(x), indem du ein Minus vor die Funktion schreibst.
3. Vergleiche die beiden Funktionen. Wenn sie gleich sind, ist die Punktsymmetrie Formel erfüllt und die Funktion ist punktsymmetrisch zum Ursprung.

Beispiel:
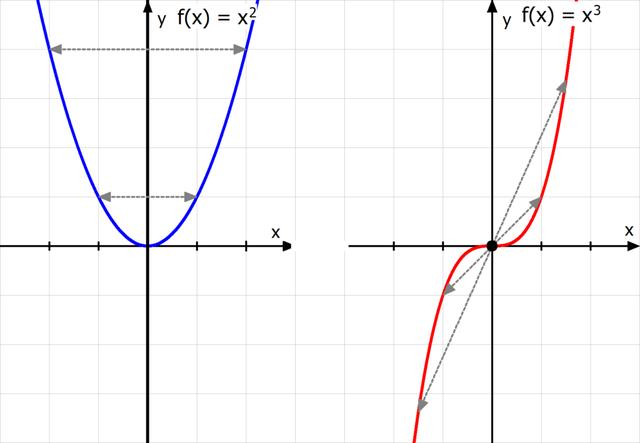
– Wenn du überprüfen sollst, ob die Funktion f(x) = x^2 punktsymmetrisch zum Ursprung ist, gehst du wie folgt vor:
1. Berechne f(-x) = (-x)^2 = x^2.
2. Berechne -f(x) = -(x^2) = -x^2.
3. Vergleiche beide Gleichungen: f(-x) = -f(x). Da sie übereinstimmen, ist die Funktion f(x) = x^2 punktsymmetrisch zum Ursprung.

Es gibt auch noch die Achsensymmetrie, bei der entlang einer bestimmten Achse gespiegelt wird. Diese solltest du für deine nächste Prüfung ebenfalls kennen.

Punktsymmetrie: Beispiele und Erklärungen zur Symmetrieeigenschaft

Was ist Punktsymmetrie?

Die Punktsymmetrie ist eine Symmetrieeigenschaft, bei der eine Figur oder Funktion um 180° gedreht werden kann, ohne ihr Aussehen zu verändern. Dabei wird die Figur um ein Spiegelzentrum oder Spiegelpunkt gedreht. Der Name „Punktsymmetrie“ leitet sich daher ab. Auch Funktionen können punktsymmetrisch zum Ursprung sein.

Beispiele für Punktsymmetrie

– Ein Quadrat ist punktsymmetrisch, da es beim Drehen um 180° auf den Kopf gestellt werden kann, ohne dass sich sein Aussehen ändert.
– Ein Parallelogramm weist ebenfalls Punktsymmetrie auf, da es als eine Art „verschobenes“ Rechteck betrachtet werden kann.
– Ein Kreis ist punktsymmetrisch zu seinem Mittelpunkt.
– Auch Funktionen können punktsymmetrisch sein. Es gibt eine Formel zur Überprüfung der Punktsymmetrie zum Ursprung.

Überprüfung der Punktsymmetrie einer Funktion

Um zu überprüfen, ob eine Funktion punktsymmetrisch zum Ursprung ist, kann man folgende Schritte befolgen:
1. Berechne f(-x), indem du alle x in der Funktion durch -x ersetzt.
2. Berechne -f(x), indem du ein Minus vor die Funktion schreibst.
3. Vergleiche die beiden Gleichungen. Wenn sie gleich sind, erfüllt die Funktion die Punktsymmetrie-Formel und ist somit punktsymmetrisch. Wenn sie nicht gleich sind, ist die Funktion nicht punktsymmetrisch zum Ursprung.

Neben der Punktsymmetrie gibt es auch noch die Achsensymmetrie, bei der eine Figur entlang einer bestimmten Achse gespiegelt wird. Es ist wichtig, beide Symmetrieeigenschaften zu kennen und unterscheiden zu können.

Schau dir das Video an, um das Thema anschaulich erklärt zu bekommen!

Punktsymmetrie: Eine anschauliche Erklärung mit konkreten Beispielen

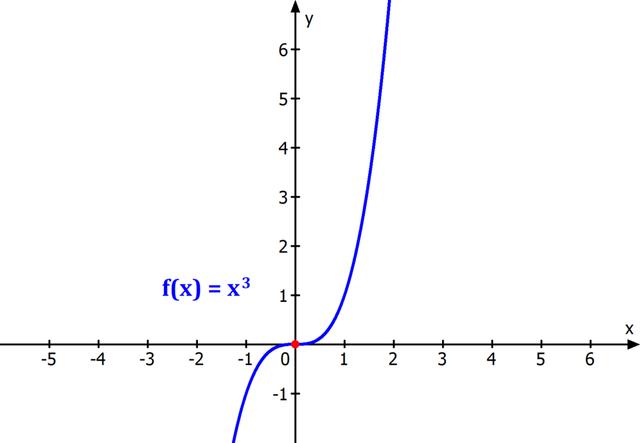
Was versteht man unter Punktsymmetrie?

Die Punktsymmetrie bezieht sich auf die Eigenschaft einer Figur oder Funktion, dass sie um 180° gedreht werden kann, ohne ihr Aussehen zu verändern. Dies bedeutet, dass die Figur oder Funktion deckungsgleich ist, wenn sie um ein Spiegelzentrum oder einen Spiegelpunkt gedreht wird. Daher kommt auch der Name Punktsymmetrie.

Beispiele für punktsymmetrische Figuren

– Ein Quadrat ist punktsymmetrisch um sein Symmetriezentrum. Wenn wir es um 180° drehen, bleibt es unverändert.
– Ein Parallelogramm weist ebenfalls Punktsymmetrie auf. Es ist eine Art „verschobenes“ Rechteck.
– Ein Kreis ist punktsymmetrisch zu seinem Mittelpunkt. Egal wie wir ihn drehen, er bleibt gleich aussehend.

Überprüfung der Punktsymmetrie bei Funktionen

Um zu überprüfen, ob eine Funktion punktsymmetrisch zum Ursprung ist, können wir eine Formel verwenden:
1. Berechne f(-x), indem du alle x in der Funktion durch -x ersetzt.
2. Berechne -f(x), indem du ein Minus vor die Funktion schreibst und die Minus-Klammer auflöst.
3. Vergleiche die beiden Gleichungen. Wenn sie gleich sind, erfüllt die Funktion die Punktsymmetrie Formel und ist punktsymmetrisch zum Ursprung.

Es gibt auch die Achsensymmetrie, bei der eine Figur oder Funktion entlang einer bestimmten Achse gespiegelt wird. Es ist wichtig, sowohl die Punktsymmetrie als auch die Achsensymmetrie zu kennen und unterscheiden zu können.

Schau dir unser Video an, um eine anschauliche Erklärung zur Punktsymmetrie zu erhalten!

Zusammenfassend lässt sich sagen, dass eine Figur punktsymmetrisch ist, wenn sie um einen bestimmten Punkt gespiegelt werden kann und dabei ihre Form beibehält. Dieses Symmetriemerkmal findet sich in vielen geometrischen Figuren wie Kreisen, Quadraten oder Dreiecken wieder und ist von grundlegender Bedeutung in der Mathematik.