Gleichungen sind mathematische Aussagen, die eine Gleichheit zwischen zwei Ausdrücken darstellen. Sie spielen eine bedeutende Rolle in der Mathematik und werden verwendet, um unbekannte Variablen zu lösen. In diesem Artikel werden wir uns mit Gleichungen befassen, ihre Bedeutung verstehen und verschiedene Methoden zur Lösung kennenlernen. Lass uns eintauchen und das Rätsel der Gleichungen entdecken!
Grundlagen der Gleichungen: Was sind mathematische Gleichungen?
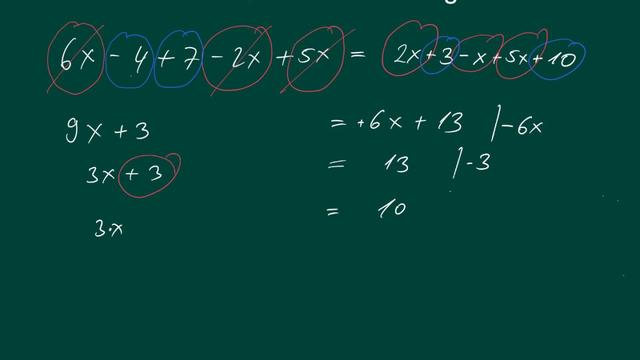
Gleichungen und ihre Bestandteile
Eine mathematische Gleichung besteht aus zwei Teilen, die durch ein Gleichheitszeichen (=) verbunden sind. Der Teil vor dem Gleichheitszeichen wird als linke Seite bezeichnet, während der Teil danach die rechte Seite ist. In einer Gleichung können sowohl Zahlen als auch Buchstaben, sogenannte Variablen, vorkommen. Variablen dienen als Platzhalter für beliebige Zahlen und beeinflussen das Ergebnis der Gleichung.
Lösungsfindung bei Gleichungen
Um herauszufinden, welche Zahl(en) für die Variable eingesetzt werden müssen, um eine richtige Aussage zu erhalten, löst man die Gleichung. Dies kann durch Äquivalenzumformungen erfolgen. Dabei werden beide Seiten der Gleichung so verändert, dass sie gleichwertig bleiben. Durch sukzessive Umformungen kann man schließlich den Wert oder die Werte ermitteln, für die die Aussage richtig ist.
Arten von mathematischen Gleichungen
Mathematische Gleichungen können in verschiedenen Formen auftreten und unterschiedliche Schwierigkeitsgrade haben. Eine einfache Form ist beispielsweise x + 4 = 6. Es gibt jedoch auch komplexere Arten von Gleichungen wie quadratische oder lineare Gleichungen. Je nach Art der Gleichung müssen spezifische Lösungsverfahren angewendet werden.
Durch das Lösen von mathematischen Gleichungen können wir unbekannte Werte ermitteln und Zusammenhänge in verschiedenen Bereichen der Mathematik verstehen.
Variablen und Lösungsmengen in Gleichungen erklärt

Was sind Variablen?
Variablen sind Buchstaben, die in mathematischen Gleichungen verwendet werden, um eine unbekannte Zahl zu repräsentieren. Sie dienen als Platzhalter für eine beliebige Zahl. In einer Gleichung können verschiedene Variablen auftreten, wie zum Beispiel x, y oder z. Indem wir verschiedenen Werten für die Variable einsetzen, können wir herausfinden, welche Zahlen die Gleichung erfüllen.
Beispiel:
In der Gleichung 2x + 5 = 15 ist x die Variable. Wenn wir verschiedene Werte für x ausprobieren, können wir feststellen, dass die Gleichung nur für x = 5 richtig ist.
Was sind Lösungsmengen?
Die Lösungsmenge einer Gleichung besteht aus den Werten, die eingesetzt werden können, um die Aussage der Gleichung wahr zu machen. Es ist die Menge aller möglichen Lösungen einer Gleichung.
Beispiel:
In der Gleichung x^2 – 4 = 0 ist die Lösungsmenge {-2, 2}. Das bedeutet, dass sowohl -2 als auch 2 eingesetzt werden können, um die Aussage der Gleichung wahr zu machen.
Es gibt verschiedene Methoden zur Lösung von Gleichungen und zur Bestimmung ihrer Lösungsmengen. Eine häufig verwendete Methode ist das Lösen durch Äquivalenzumformungen. Dabei werden auf beiden Seiten der Gleichung gleiche Operationen ausgeführt, um die Variable isoliert auf einer Seite zu haben.
Es ist wichtig zu beachten, dass nicht alle Gleichungen eine Lösung haben. Manchmal kann die Lösungsmenge leer sein oder unendlich viele Elemente enthalten.
Zusammenfassend sind Variablen in Gleichungen Platzhalter für unbekannte Zahlen und die Lösungsmenge besteht aus den Werten, die eingesetzt werden können, um die Aussage der Gleichung wahr zu machen. Durch verschiedene Methoden wie Äquivalenzumformungen können wir Gleichungen lösen und ihre Lösungsmengen bestimmen.
Arten von Gleichungen: Mehr als nur x + 4 = 6

Lineare Gleichungen:
Eine lineare Gleichung ist eine Gleichung, bei der die höchste Potenz der Variablen 1 ist. Das bedeutet, dass die Variable nicht quadriert oder mit einer höheren Potenz vorkommt. Ein Beispiel für eine lineare Gleichung ist 2x + 3 = 7.
Quadratische Gleichungen:
Eine quadratische Gleichung ist eine Gleichung, bei der die höchste Potenz der Variablen 2 ist. Sie hat also die Form ax^2 + bx + c = 0, wobei a, b und c Konstanten sind. Um eine quadratische Gleichung zu lösen, kann man die sogenannte quadratische Lösungsformel verwenden: x = (-b ± √(b^2 – 4ac)) / (2a).
Kubische Gleichungen:
Eine kubische Gleichung ist eine Gleichung, bei der die höchste Potenz der Variablen 3 ist. Sie hat also die Form ax^3 + bx^2 + cx + d = 0. Kubische Gleichungen können oft schwieriger zu lösen sein als lineare oder quadratische Gleichungen und erfordern manchmal spezielle Lösungsverfahren.
Es gibt noch viele weitere Arten von Gleichungen, wie zum Beispiel exponentielle oder logarithmische Gleichungen. Jede Art von Gleichung hat ihre eigenen Lösungsverfahren und Eigenschaften. Es lohnt sich also, sich mit den verschiedenen Arten von Gleichungen vertraut zu machen, um sie erfolgreich lösen zu können.
Schritt-für-Schritt-Anleitung zur Lösung von Gleichungen
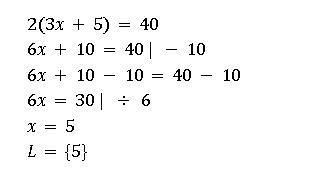
Schritt 1: Sammle alle Variablen auf einer Seite
Um eine Gleichung zu lösen, ist es oft hilfreich, alle Variablen auf einer Seite der Gleichung zu haben. Du kannst dies erreichen, indem du Terme von einer Seite auf die andere Seite bringst. Achte dabei darauf, das Vorzeichen der Terme zu ändern.
Beispiel:
x + 4 = 6
Subtrahiere 4 von beiden Seiten der Gleichung:
x + 4 – 4 = 6 – 4
Das ergibt:
x = 2
Schritt 2: Vereinfache die Gleichung
Manchmal musst du die Gleichung weiter vereinfachen, um die Lösung zu finden. Dies kann beinhalten, dass du Terme zusammenfasst oder ausklammerst.
Beispiel:
2x + 3 = x + 7
Subtrahiere x von beiden Seiten der Gleichung:
2x – x + 3 = x – x + 7
Das ergibt:
x + 3 = 7
Schritt 3: Isoliere die Variable
Um die Variable zu isolieren und die Lösung zu finden, musst du möglicherweise weitere Äquivalenzumformungen durchführen.
Beispiel:
x + 3 = 7
Subtrahiere 3 von beiden Seiten der Gleichung:
x + 3 – 3 = 7 – 3
Das ergibt:
x = 4
Äquivalenzumformung: Der Schlüssel zum Lösen von Gleichungen

Was ist Äquivalenzumformung?
Die Äquivalenzumformung ist eine Methode, die verwendet wird, um Gleichungen zu lösen. Dabei werden mathematische Operationen auf beiden Seiten der Gleichung durchgeführt, um sie in eine äquivalente Form umzuwandeln. Das bedeutet, dass die Lösung der ursprünglichen Gleichung auch die Lösung der umgeformten Gleichung ist.
Wie wendet man Äquivalenzumformungen an?
Um eine Gleichung mit Äquivalenzumformungen zu lösen, müssen verschiedene Schritte befolgt werden. Hier sind einige häufig verwendete Äquivalenzumformungen:
– Addition oder Subtraktion: Du kannst einen Wert zu beiden Seiten der Gleichung addieren oder subtrahieren.
– Multiplikation oder Division: Du kannst beide Seiten der Gleichung mit demselben Wert multiplizieren oder dividieren.
– Umkehren: Du kannst beide Seiten der Gleichung umkehren, indem du sie negierst (positive Zahlen werden zu negativen und umgekehrt).
– Vereinfachen: Du kannst Terme auf beiden Seiten zusammenfassen oder ausklammern, um die Gleichung zu vereinfachen.
Es ist wichtig zu beachten, dass du immer dieselbe Operation auf beiden Seiten der Gleichung durchführen musst, um die Äquivalenz beizubehalten. Dadurch bleibt das Ergebnis korrekt und die Lösungen bleiben gleich.
Durch das Anwenden von Äquivalenzumformungen kannst du schrittweise die Lösung einer Gleichung finden, indem du die Variable isolierst. Am Ende erhältst du eine Gleichung, in der die Variable alleine auf einer Seite steht und somit leicht abgelesen werden kann.
Es ist ratsam, Übungsaufgaben zu lösen und verschiedene Beispiele zu bearbeiten, um ein besseres Verständnis für Äquivalenzumformungen und das Lösen von Gleichungen zu entwickeln.
Durch Ausprobieren zur Lösung: Einfache Gleichungen lösen

Beispiel:
Angenommen, wir haben die Gleichung x + 4 = 6. Wir möchten herausfinden, welchen Wert x haben muss, damit die Aussage richtig ist.
Schritt 1: Setze einen Wert für x ein und überprüfe, ob die Aussage richtig ist. Beginnen wir mit x = 1.
- x + 4 = 6
- 1 + 4 = 6
- 5 = 6
Da die Aussage nicht richtig ist, wissen wir, dass x = 1 keine Lösung ist.
Schritt 2: Setze den nächsten Wert für x ein und überprüfe erneut. Lass uns x = 2 ausprobieren.
- x + 4 = 6
- 2 + 4 = 6
- 6 = 6
In diesem Fall ist die Aussage wahr, also wissen wir, dass x = 2 eine Lösung der Gleichung ist.
Schritt 3: Du kannst diesen Schritt fortsetzen und weitere Werte für x ausprobieren, um sicherzustellen, dass es keine weiteren Lösungen gibt. In diesem Fall haben wir bereits festgestellt, dass x = 2 die einzige Lösung ist.
Durch Ausprobieren verschiedener Werte können wir also herausfinden, welche Zahl für die Variable in der Gleichung eingesetzt werden muss, um eine richtige Aussage zu erhalten.
Zusammenfassend sind Gleichungen mathematische Aussagen, bei denen zwei Ausdrücke miteinander verglichen werden. Sie dienen dazu, Unbekannte zu berechnen und Probleme in verschiedenen Bereichen wie Algebra, Physik und Wirtschaft zu lösen. Das Verständnis von Gleichungen ist daher für das mathematische Denken und die Anwendung in der realen Welt von großer Bedeutung.

