Was ist eine Primzahl? Entdecke die Grundlagen und Eigenschaften!

Eine Primzahl ist eine natürliche Zahl größer als 1, die nur durch 1 und sich selbst ohne Rest teilbar ist. Sie spielt eine wichtige Rolle in der Mathematik und findet Anwendung in verschiedenen Bereichen wie Kryptographie und Zahlentheorie. Erfahren Sie hier mehr über die Eigenschaften und Bedeutung von Primzahlen.

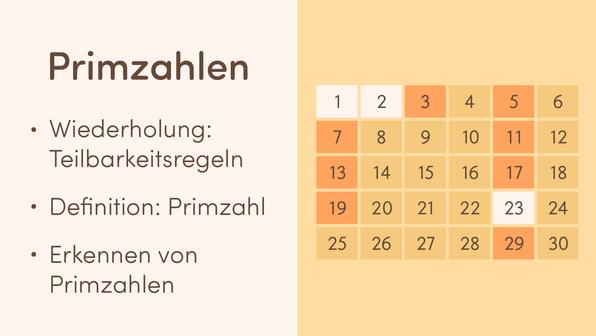
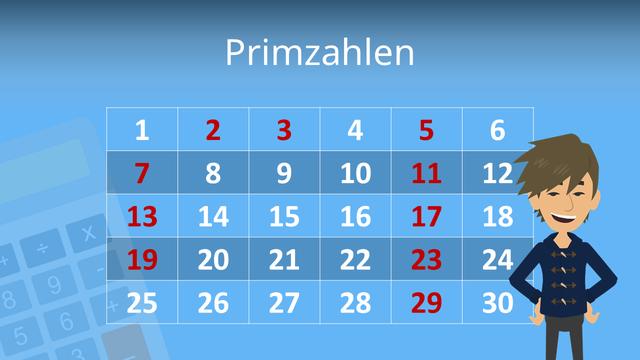
Was sind Primzahlen und wie erkennt man sie?

Primzahlen sind natürliche Zahlen, die genau zwei Teiler haben: sich selbst und 1. Sie können nicht durch andere Zahlen ohne Rest geteilt werden. Ein Beispiel für eine Primzahl ist die Zahl 5, da sie nur durch 1 und 5 teilbar ist. Im Gegensatz dazu ist die Zahl 4 keine Primzahl, da sie neben den Teilern 1 und 4 auch noch durch 2 teilbar ist.

Um zu erkennen, ob eine Zahl eine Primzahl ist, kannst du versuchen, sie durch andere Zahlen als 1 oder sich selbst zu teilen. Wenn dir das nicht gelingt, handelt es sich um eine Primzahl.

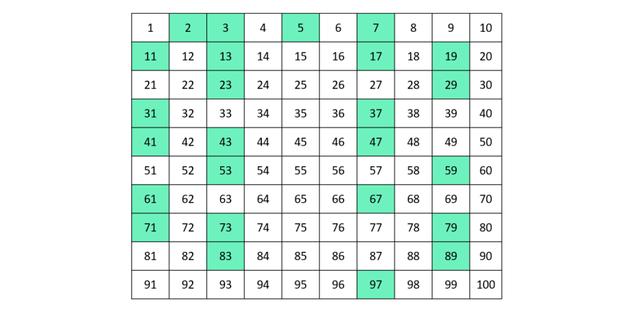
Es gibt verschiedene Methoden zur Bestimmung von Primzahlen. Eine bekannte Methode ist das Sieb des Eratosthenes, mit dem man Primzahlen bis zu einer bestimmten Grenze finden kann. Eine andere Methode ist die Faktorisierung einer Zahl in ihre Primfaktoren. Dabei zerlegt man eine Zahl in ein Produkt aus Primzahlen.

Primzahlen spielen nicht nur in der Mathematik eine wichtige Rolle, sondern haben auch praktische Anwendungen. In der Kryptographie werden beispielsweise große Primzahlen verwendet, um Daten sicher zu verschlüsseln. Außerdem ermöglicht die Eigenschaft von Primzahlen, dass jede natürliche Zahl entweder eine Primzahl ist oder in ein Produkt aus Primzahlen zerlegt werden kann (Fundamentalsatz der Arithmetik), verschiedene Berechnungen wie die Bestimmung des größten gemeinsamen Teilers oder des kleinsten gemeinsamen Vielfachen.

Die Identifizierung von Primzahlen hat also sowohl theoretische als auch praktische Bedeutung und ist ein grundlegendes Konzept in der Mathematik.

Die Bedeutung von Primzahlen in der Mathematik

Primzahlen als Grundbausteine der Zahlenwelt

Primzahlen spielen eine fundamentale Rolle in der Mathematik, da sie als Grundbausteine der Zahlenwelt angesehen werden. Jede natürliche Zahl größer als 1 kann entweder selbst eine Primzahl sein oder als Produkt von Primzahlen dargestellt werden. Dieses Konzept wird als Primfaktorzerlegung bezeichnet und ist ein wichtiger Bestandteil vieler mathematischer Verfahren.

Eindeutigkeit der Primfaktorzerlegung

Die Primfaktorzerlegung einer Zahl ist eindeutig, unabhängig von der Reihenfolge der Faktoren. Das bedeutet, dass jede Zahl nur auf eine einzige Weise als Produkt von Primzahlen dargestellt werden kann. Dieses Konzept ermöglicht es uns, den größten gemeinsamen Teiler zweier Zahlen zu finden und spielt auch eine Rolle bei der Berechnung des kleinsten gemeinsamen Vielfachen.

Anwendungen in der Kryptographie

In der Kryptographie sind Primzahlen von großer Bedeutung für die Verschlüsselung von Daten. Das RSA-Verfahren basiert zum Beispiel darauf, schnell große Primzahlen zu finden. Durch die Verwendung von Primzahlen können komplexe Verschlüsselungsverfahren entwickelt werden, die sicherer vor unbefugtem Zugriff sind.

Weitere Anwendungsbereiche

Primzahlen haben auch in anderen Bereichen Anwendungen. Zum Beispiel werden sie in Algorithmen zur Datenkompression und in der Zahlentheorie verwendet. Sie dienen auch als Grundlage für die Entwicklung von Codes und Verschlüsselungstechniken.

Primzahlen bis 1000

Wenn du mehr über Primzahlen bis 1000 erfahren möchtest, haben wir einen speziellen Beitrag für dich vorbereitet. Dort findest du eine Liste aller Primzahlen bis 1000 und weitere Informationen zu ihrer Bedeutung in der Mathematik.

Primzahlzwillinge und Primzahldrillinge: Besondere Eigenschaften von Primzahlen

Primzahlzwillinge

Primzahlzwillinge sind zwei aufeinanderfolgende Primzahlen, die einen Abstand von 2 haben. Das bedeutet, dass zwischen den beiden Primzahlen keine anderen Primzahlen existieren. Ein Beispiel für ein Primzahlzwillingpaar ist 3 und 5, da sie beide Primzahlen sind und nur eine natürliche Zahl (4) zwischen ihnen liegt. Es ist jedoch unbekannt, ob es unendlich viele Primzahlzwillinge gibt oder ob es einen größten bekannten Abstand zwischen zwei Primzahlpärchen gibt.

Beispiele für weitere Primzahlzwillingpaare sind:
– (11, 13)
– (17, 19)
– (29, 31)

Primzahldrillinge

Primzahldrillinge sind drei aufeinanderfolgende Primzahlen, die alle denselben Abstand von 2 zueinander haben. Das bedeutet, dass zwischen den drei Primzahlen keine weiteren Primzahlen existieren. Ein Beispiel für einen Primzahldrilling ist (3, 5, 7), da sie alle prim sind und jeweils einen Abstand von 2 voneinander haben.

Es ist bekannt, dass der einzige bekannte Primzahldrilling (3, 5, 7) ist. Es ist jedoch nicht bewiesen worden, ob es unendlich viele solcher Drillinge gibt oder ob es andere mögliche Kombinationen von drei aufeinanderfolgenden primen Zahlen mit einem Abstand von genau 2 gibt.

Zusammenfassend sind Primzahlzwillinge und Primzahldrillinge besondere Eigenschaften von Primzahlen, die in der Mathematik von Interesse sind. Ihre genaue Verteilung und Anzahl sind jedoch noch nicht vollständig erforscht.

Die Primfaktorzerlegung: Wie man eine Zahl in Primfaktoren zerlegt

Die Primfaktorzerlegung ist ein mathematisches Verfahren, bei dem eine Zahl in ihre kleinsten Primfaktoren zerlegt wird. Dabei werden die Teiler einer Zahl ermittelt, bis nur noch Primzahlen übrig bleiben.

Wie funktioniert die Primfaktorzerlegung?

Um eine Zahl in Primfaktoren zu zerlegen, beginnt man mit der kleinsten Primzahl und versucht diese als Teiler der gegebenen Zahl zu verwenden. Wenn die Zahl durch diese Primzahl teilbar ist, wird sie durch diese geteilt und der Vorgang wird wiederholt, bis keine weiteren Teiler gefunden werden können. Die erhaltenen Primzahlen sind dann die Faktoren der ursprünglichen Zahl.

Beispiel:
Um die Zahl 30 in ihre Primfaktoren zu zerlegen, startet man mit der kleinsten Primzahl 2. Da 30 durch 2 teilbar ist, ergibt sich als Ergebnis 15. Nun versucht man erneut, die neue Zahl (15) durch die kleinste Primzahl (2) zu teilen. Da dies nicht möglich ist, geht man zur nächsten größeren Primzahl über, in diesem Fall 3. Da 15 durch 3 teilbar ist, ergibt sich als neues Ergebnis 5. Da dies bereits eine Primzahl ist, kann man den Vorgang beenden.

Die Primfaktorzerlegung von 30 lautet also: 2 * 3 * 5.

Warum ist die Primfaktorzerlegung wichtig?

Die Primfaktorzerlegung hat verschiedene Anwendungen in der Mathematik. Zum einen ermöglicht sie es, den größten gemeinsamen Teiler zweier Zahlen zu finden. Dies ist hilfreich bei der Vereinfachung von Brüchen oder dem Lösen von Gleichungen.

Darüber hinaus ist die Primfaktorzerlegung auch in der Kryptographie von großer Bedeutung. Hier werden große Primzahlen verwendet, um Daten sicher zu verschlüsseln und zu entschlüsseln.

Die Primfaktorzerlegung ist also ein wichtiges mathematisches Verfahren, das sowohl in der Schulmathematik als auch in verschiedenen Anwendungsbereichen eine Rolle spielt.

Die Anwendung von Primzahlen in der Kryptographie

RSA-Verfahren

Das RSA-Verfahren ist ein Verschlüsselungsalgorithmus, der auf der Verwendung von Primzahlen basiert. Bei diesem Verfahren werden zwei große Primzahlen ausgewählt und miteinander multipliziert, um ein Produkt zu erzeugen. Diese beiden Primzahlen dienen als Schlüssel für die Verschlüsselung und Entschlüsselung von Daten. Die Sicherheit des RSA-Verfahrens beruht darauf, dass es sehr schwierig ist, das Produkt der beiden Primzahlen zu faktorisieren und somit die ursprünglichen Primzahlen zu berechnen.

Sicherheit in der Kryptographie

Primzahlen spielen auch eine wichtige Rolle bei der Sicherheit anderer kryptographischer Verfahren. Zum Beispiel werden sie verwendet, um sichere Schlüssel zu generieren, die für die Verschlüsselung und Entschlüsselung von Daten verwendet werden. Durch die Wahl großer Primzahlen als Basis für diese Schlüssel wird es praktisch unmöglich gemacht, den privaten Schlüssel aus dem öffentlichen Schlüssel abzuleiten.

Weitere Anwendungen

Neben dem RSA-Verfahren und der Generierung sicherer Schlüssel haben Primzahlen auch in anderen Bereichen der Kryptographie Anwendungen. Sie werden beispielsweise zur Erzeugung von Zufallszahlen verwendet, die für verschiedene kryptographische Zwecke benötigt werden. Darüber hinaus spielen sie eine Rolle bei der Prüfung auf Primzahlentestbarkeit von Zahlen und bei der Berechnung des größten gemeinsamen Teilers zweier Zahlen.

Insgesamt sind Primzahlen ein wesentlicher Bestandteil vieler kryptographischer Verfahren und spielen eine entscheidende Rolle bei der Gewährleistung der Sicherheit von Daten und Kommunikation.

Warum ist 0 keine Primzahl? Eine Erklärung zur Definition von Primzahlen

Was sind Primzahlen?

Primzahlen sind natürliche Zahlen größer als 1, die genau zwei Teiler haben: sich selbst und die Zahl 1. Sie können nicht durch andere Zahlen ohne Rest geteilt werden. Ein Beispiel für eine Primzahl ist die Zahl 5, da sie nur durch 1 und 5 ohne Rest teilbar ist.

Warum ist 0 keine Primzahl?

Die Zahl 0 erfüllt nicht die Voraussetzung einer Primzahl, dass sie genau zwei Teiler hat. Da es nicht erlaubt ist, Zahlen durch 0 zu teilen, kann man bei der Zahl 0 keinen zweiten Teiler finden. Daher wird die Zahl 0 nicht als Primzahl betrachtet.

Warum gibt es unendlich viele Primzahlen?

Der antike Mathematiker Euklid hat vor über 2000 Jahren bewiesen, dass es unendlich viele Primzahlen gibt. Sein Beweis basiert auf dem Widerspruchsprinzip: Angenommen, es gäbe nur endlich viele Primzahlen. Dann könnte man eine neue Zahl bilden, indem man alle bekannten Primzahlen multipliziert und eins addiert. Diese neue Zahl wäre entweder eine weitere Primzahl oder hätte einen neuen Teiler, der bisher noch nicht bekannt ist. In beiden Fällen würde dies zeigen, dass es doch mehr als endlich viele Primzahlen gibt.

Daher kann man sagen, dass es unendlich viele Primzahlen gibt und die Liste der bekannten Primzahlen immer weiter wächst.

Warum ist die Zahl 1 keine Primzahl?

Die Zahl 1 erfüllt nicht die Definition einer Primzahl, da sie nur einen Teiler hat: sich selbst. Eine Primzahl muss jedoch genau zwei Teiler haben, nämlich sich selbst und die Zahl 1. Daher wird die Zahl 1 nicht als Primzahl betrachtet.

Warum sind Primzahlen wichtig?

Primzahlen spielen eine wichtige Rolle in verschiedenen mathematischen Verfahren und Anwendungen. Sie werden zum Beispiel bei der Verschlüsselung von Daten in der Kryptographie verwendet, wie beim RSA-Verfahren. Auch bei der Faktorisierung von Zahlen, dem Finden des größten gemeinsamen Teilers oder dem Berechnen des kleinsten gemeinsamen Vielfachen kommen Primzahlen zum Einsatz.

Durch das Studium von Primzahlen können Mathematiker neue Erkenntnisse gewinnen und diese auf verschiedene Bereiche anwenden. Deshalb ist das Verständnis von Primzahlen für viele mathematische Konzepte und Anwendungen unerlässlich.

Zusammenfassend ist eine Primzahl eine natürliche Zahl größer als 1, die nur durch 1 und sich selbst ohne Rest teilbar ist. Sie spielen eine wichtige Rolle in der Mathematik und haben verschiedene Anwendungen, insbesondere in der Kryptographie. Das Verständnis von Primzahlen ermöglicht es uns, komplexe mathematische Konzepte zu erforschen und zu entwickeln.