Bruchrechnung leicht gemacht: So rechnet man Brüche richtig!

„In diesem Artikel geht es darum, wie man Brüche richtig berechnet. Egal ob Addition, Subtraktion, Multiplikation oder Division von Brüchen – wir zeigen Ihnen Schritt für Schritt, wie Sie die richtige Lösung erhalten. Einfach und verständlich erklärt, werden Sie in kürzester Zeit zum Experten im Rechnen mit Brüchen!“

Grundlagen der Bruchrechnung: Wie rechnet man Brüche?

Die Bruchrechnung ist eine wichtige mathematische Grundlage, die uns hilft, Teile von Ganzen zu beschreiben. Ein Bruch besteht aus einem Zähler (oben), einem Nenner (unten) und einem Bruchstrich dazwischen. Der Zähler gibt an, wie viele Teile wir haben, während der Nenner angibt, in wie viele gleich große Teile das Ganze geteilt ist.

Ein Bruch mit dem gleichen Zähler und Nenner hat einen Wert von 1 und repräsentiert somit ein Ganzes. Je größer der Nenner ist, desto feiner unterteilen wir das Ganze.

Um mit Brüchen zu rechnen, können wir die vier Grundrechenarten verwenden. Bei der Addition und Subtraktion müssen die Nenner gleich sein, während bei der Multiplikation und Division dies keine Rolle spielt.

Wir können Brüche auch kürzen oder erweitern. Beim Kürzen teilen wir sowohl den Zähler als auch den Nenner durch die gleiche Zahl, um den Bruch zu vereinfachen. Beim Erweitern multiplizieren wir sowohl den Zähler als auch den Nenner mit derselben Zahl, um den Bruch zu vergrößern.

Es ist wichtig zu beachten, dass es echte und unechte Brüche gibt. Ein echter Bruch hat einen Zähler kleiner als den Nenner, während ein unechter Bruch einen Zähler hat, der größer oder gleich groß wie der Nenner ist.

Die Grundlagen der Bruchrechnung sind wichtig, um in verschiedenen mathematischen Problemen und im Alltag richtig rechnen zu können. Es ist ratsam, das Rechnen mit Brüchen durch Übungsaufgaben weiter zu festigen.

Schritt-für-Schritt Anleitung: So rechnet man mit Brüchen

Addition und Subtraktion von Brüchen mit gleichem Nenner:

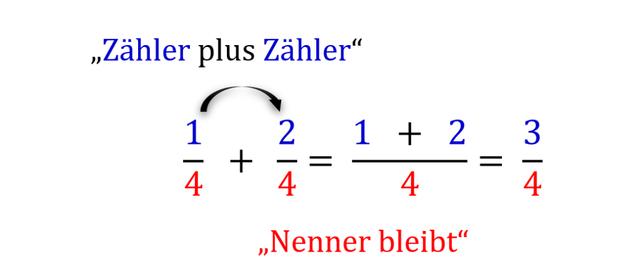
– Um Brüche mit dem gleichen Nenner zu addieren, addiere einfach die Zähler und lasse den Nenner unverändert.
– Beispiel: 1/4 + 2/4 = 3/4
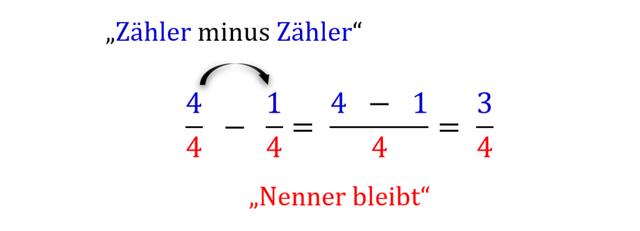
– Um Brüche mit dem gleichen Nenner zu subtrahieren, subtrahiere einfach die Zähler und lasse den Nenner unverändert.
– Beispiel: 5/6 – 2/6 = 3/6

Addition und Subtraktion von Brüchen mit ungleichem Nenner:

– Um Brüche mit unterschiedlichen Nennern zu addieren oder zu subtrahieren, musst du sie auf einen gemeinsamen Nenner bringen.
– Finde den kleinsten gemeinsamen Vielfachen (kgV) der beiden Nenner.
– Erweitere die Brüche jeweils so, dass sie den gemeinsamen Nenner haben.
– Führe dann die Addition oder Subtraktion wie bei gleichnamigen Brüchen durch.
– Beispiel: 1/3 + 1/4 = (4/12) + (3/12) = 7/12

Multiplikation von Brüchen:

– Multipliziere einfach die Zähler miteinander und die Nenner miteinander.
– Beispiel: (2/5) * (3/4) = (2*3)/(5*4) = 6/20

Division von Brüchen:

– Kehre den zweiten Bruch um, indem du Zähler und Nenner vertauschst.
– Multipliziere dann die beiden Brüche wie bei der Multiplikation.
– Beispiel: (2/3) / (4/5) = (2/3) * (5/4) = (2*5)/(3*4) = 10/12

Kürzen von Brüchen:

– Teile den Zähler und den Nenner durch den größten gemeinsamen Teiler (ggT).
– Der ggT ist die größte Zahl, durch die sowohl der Zähler als auch der Nenner ohne Rest teilbar sind.
– Beispiel: 8/12 kann gekürzt werden zu 2/3, da der ggT von 8 und 12 gleich 4 ist.

Erweitern von Brüchen:

– Multipliziere den Zähler und den Nenner mit einer geeigneten Zahl, um einen gewünschten Nenner zu erhalten.
– Beispiel: 1/2 kann erweitert werden auf 3/6, indem man Zähler und Nenner mit 3 multipliziert.

Bruchrechnung leicht erklärt: Rechenregeln und Beispiele

Rechenregeln für Bruchrechnung:

– Brüche mit gleichem Nenner können addiert oder subtrahiert werden, indem man die Zähler addiert oder subtrahiert und den Nenner beibehält.
– Bei der Multiplikation von Brüchen multipliziert man die Zähler miteinander und die Nenner miteinander.
– Bei der Division von Brüchen tauscht man den Zähler des zweiten Bruchs mit dem Nenner und multipliziert dann wie bei der Multiplikation.

Beispiele für Bruchrechnung:

1. Addition:
– 1/4 + 1/4 = 2/4 = 1/2 (gleicher Nenner)
– 1/3 + 1/6 = 2/6 + 1/6 = 3/6 = 1/2 (ungleicher Nenner, vorher auf gleichen Nenner gebracht)

2. Subtraktion:
– 5/8 – 3/8 = 2/8 = 1/4 (gleicher Nenner)
– 7/10 – 2/5 = (7*5)/(10*5) – (2*10)/(5*10) = 35/50 -20/50 =15/50=3 /10 (ungleicher Nenner, vorher auf gleichen Nenner gebracht)

3. Multiplikation:
– (1/2) * (3/4) = (1*3)/(2*4) = 3/8

4. Division:
– (2/3) / (1/5) = (2/3) * (5/1) = (2*5)/(3*1) = 10/3

Wie funktioniert das Rechnen mit Brüchen? Eine einfache Erklärung

Das Rechnen mit Brüchen ist gar nicht so kompliziert, wie es auf den ersten Blick scheinen mag. Hier ist eine einfache Erklärung, wie du mit Brüchen rechnen kannst:

1. Addition und Subtraktion von Brüchen:
– Um Brüche mit dem gleichen Nenner zu addieren oder zu subtrahieren, addierst bzw. subtrahierst du einfach die Zähler und lässt den Nenner unverändert.
– Wenn die Brüche unterschiedliche Nenner haben, musst du sie zuerst auf einen gemeinsamen Nenner bringen, indem du sie erweiterst oder kürzt.

2. Multiplikation von Brüchen:
– Um zwei Brüche zu multiplizieren, multiplizierst du einfach die Zähler miteinander und die Nenner miteinander.
– Wenn einer der Faktoren ein ganzer Zahl ist, wandelst du diese Zahl in einen Bruch um, indem du sie über 1 schreibst (z.B. 3 wird zu 3/1) und dann wie gewohnt multiplizierst.

3. Division von Brüchen:
– Um zwei Brüche zu dividieren, vertauschst du den Zähler des zweiten Bruchs mit seinem Nenner und multiplizierst dann wie bei der Multiplikation.
– Wenn einer der Faktoren ein ganzer Zahl ist, wandelst du diese Zahl in einen Bruch um, indem du sie über 1 schreibst (z.B. 4 wird zu 4/1) und dann wie gewohnt dividierst.

Es ist auch wichtig zu beachten, dass Brüche gekürzt oder erweitert werden können, um sie einfacher darzustellen. Dazu teilst oder multiplizierst du den Zähler und den Nenner mit derselben Zahl.

Mit diesen einfachen Regeln kannst du problemlos mit Brüchen rechnen. Übe am besten anhand von Beispielaufgaben, um sicherer im Umgang mit Brüchen zu werden.

Bruchrechnung verstehen und anwenden: Tipps und Tricks

Die Bruchrechnung ist ein wichtiger Teil der Mathematik und kann in vielen Situationen angewendet werden. Hier sind einige Tipps und Tricks, die dir helfen können, die Bruchrechnung besser zu verstehen und anzuwenden:

Gleichnamige und ungleichnamige Brüche

Es gibt zwei Arten von Brüchen: gleichnamige und ungleichnamige Brüche. Gleichnamige Brüche haben den gleichen Nenner, während ungleichnamige Brüche verschiedene Nenner haben. Beim Addieren oder Subtrahieren von Brüchen müssen die Nenner gleich sein. Wenn sie es nicht sind, musst du die Brüche auf einen gemeinsamen Nenner bringen.

Kürzen und Erweitern von Brüchen

Du kannst einen Bruch kürzen, indem du Zähler und Nenner durch dieselbe Zahl teilst. Dadurch wird der Bruch vereinfacht, behält aber seinen Wert bei. Um einen Bruch zu erweitern, multiplizierst du Zähler und Nenner mit derselben Zahl. Dadurch wird der Wert des Bruchs größer, aber er bleibt immer noch derselbe.

Rechenoperationen mit Brüchen

Du kannst mit Brüchen genauso rechnen wie mit ganzen Zahlen. Bei der Addition oder Subtraktion addierst bzw. subtrahierst du die Zähler der Brüche, während der Nenner gleich bleibt. Bei der Multiplikation multiplizierst du die Zähler und die Nenner der Brüche. Bei der Division vertauschst du den Zähler und den Nenner des zweiten Bruchs und multiplizierst dann.

Üben, üben, üben

Um die Bruchrechnung wirklich zu beherrschen, ist Übung entscheidend. Löse so viele Aufgaben wie möglich und versuche verschiedene Arten von Bruchrechnungen zu verstehen. Je mehr du übst, desto sicherer wirst du im Umgang mit Brüchen.

Praktische Anwendungen

Die Bruchrechnung hat auch praktische Anwendungen im Alltag. Zum Beispiel kannst du mit Brüchen Rezepte umrechnen oder Teile eines Ganzen beschreiben. Indem du die Bruchrechnung anwendest, kannst du Probleme in verschiedenen Situationen lösen.

Die Bruchrechnung kann am Anfang etwas kompliziert erscheinen, aber mit Übung und Verständnis wirst du sie beherrschen. Nutze diese Tipps und Tricks, um deine Fähigkeiten in der Bruchrechnung zu verbessern und erfolgreich damit umzugehen.

Praktische Anwendung von Bruchrechnung: Warum ist es wichtig, Brüche zu beherrschen?

Alltag:

– In vielen Alltagssituationen begegnen uns Brüche. Zum Beispiel beim Kochen, wenn wir Rezepte umrechnen müssen oder wenn wir Mengen in unterschiedliche Portionen aufteilen möchten.
– Auch im Handel werden Brüche verwendet, zum Beispiel bei der Angabe von Preisen pro Kilogramm oder Liter.
– Beim Bauen und Heimwerken können Brüche verwendet werden, um Maße genau anzugeben.

Beruflich:

– In vielen Berufen ist das Verständnis und die Anwendung von Bruchrechnung notwendig. Zum Beispiel in der Gastronomie, im Handwerk oder in technischen Berufen.
– Auch in wissenschaftlichen Bereichen wie der Physik oder Chemie werden oft Brüche verwendet.

Weiterführende Mathematik:

– Die Beherrschung von Bruchrechnung ist eine Grundlage für weiterführende mathematische Themen wie Algebra und Analysis.
– In der Geometrie können Brüche verwendet werden, um Flächenanteile oder Verhältnisse darzustellen.

Es gibt also viele praktische Anwendungen für die Beherrschung von Bruchrechnung sowohl im Alltag als auch beruflich und in weiterführenden mathematischen Themen. Es lohnt sich daher, diese Grundlagen gut zu verstehen und anzuwenden.

Insgesamt kann gesagt werden, dass das Rechnen mit Brüchen durch die Anwendung geeigneter Methoden und Regeln erlernt werden kann. Durch das Verständnis der Grundlagen wie dem Kürzen oder Erweitern von Brüchen sowie dem Umgang mit den verschiedenen Rechenoperationen lassen sich Bruchaufgaben erfolgreich lösen. Es ist wichtig, ausreichend Übung und Geduld aufzubringen, um diese Fähigkeiten zu festigen und anzuwenden. Mit der Zeit wird das Rechnen mit Brüchen immer einfacher und ermöglicht es, mathematische Probleme präzise und genau zu lösen.