Wie multipliziert man Brüche effektiv?

In diesem Artikel geht es darum, wie man Brüche multipliziert. Brüche sind mathematische Ausdrücke, die uns helfen, Teile von Ganzen zu beschreiben. Das Multiplizieren von Brüchen kann manchmal verwirrend sein, aber mit den richtigen Schritten und ein wenig Übung ist es ganz einfach. In diesem Artikel werden wir die Grundlagen des Bruchmultiplikation erklären und einige Beispiele geben, um das Konzept besser zu verdeutlichen. Lass uns loslegen!

Grundlagen der Bruchmultiplikation: Wie multipliziert man Brüche richtig?

Bruchrechnung mit ganzen Zahlen

Beim Multiplizieren von Brüchen mit ganzen Zahlen ist es wichtig, die Zahl zuerst in einen Bruch umzuwandeln. Dazu schreibt man die ganze Zahl als Zähler auf den Bruchstrich und den Nenner als 1. Anschließend multipliziert man den Zähler des Bruchs mit dem Zähler der anderen Zahl und den Nenner des Bruchs mit dem Nenner der anderen Zahl. Das Ergebnis kann anschließend gekürzt werden, falls möglich.

Beispiel:
3 * 2/5 = 6/5

Bruchrechnung mit gemischten Zahlen

Wenn man gemischte Brüche multiplizieren möchte, muss man sie zuerst in einen unechten Bruch umwandeln. Dazu multipliziert man die ganze Zahl mit dem Nenner und addiert den Zähler dazu. Der Nenner bleibt unverändert. Anschließend kann man wie gewohnt die beiden Brüche multiplizieren und das Ergebnis kürzen, falls möglich.

Beispiel:
2 1/3 * 4/5 = (2 * 3 + 1) / 3 * 4/5 = 7/3 * 4/5 = 28/15

Kürzen von Brüchen

Um einen Bruch zu kürzen, müssen Zähler und Nenner einen gemeinsamen Teiler haben. Man teilt sowohl den Zähler als auch den Nenner durch dieselbe Zahl. Dadurch wird der Bruch vereinfacht. Es ist ratsam, bereits vor dem Multiplizieren zu kürzen, um das Rechnen mit großen Zahlen zu vermeiden.

Zusätzlich kann man beim Multiplizieren von Brüchen auch über Kreuz kürzen, indem man die Zähler mit den jeweils gegenüberliegenden Nennern kürzt.

Beispiel:
8/12 * 3/4 = (8 * 3) / (12 * 4) = 24/48 = 1/2

Schritt-für-Schritt Anleitung zur Multiplikation von Brüchen

1. Multiplizieren der Zähler und Nenner

– Um zwei Brüche zu multiplizieren, multiplizierst du den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs.
– Anschließend multiplizierst du den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs.

Beispiel:
1/3 * 2/5
Zähler: 1 * 2 = 2
Nenner: 3 * 5 = 15

Das Ergebnis ist also 2/15.

2. Umwandeln von ganzen Zahlen in Brüche

– Wenn du einen Bruch mit einer ganzen Zahl multiplizieren möchtest, musst du die Zahl zuerst in einen Bruch umwandeln.
– Schreibe die ganze Zahl als Zähler auf den Bruchstrich und setze den Nenner auf 1.

Beispiel:
3 * 1/4
Umwandlung der Zahl 3 in einen Bruch:
Zähler: 3 * 1 = 3
Nenner: 1

Das Ergebnis ist also 3/4.

3. Umformen von gemischten Zahlen in Brüche

– Wenn du einen gemischten Bruch multiplizieren möchtest, musst du ihn zuerst in einen unechten (normalen) Bruch umwandeln.
– Multipliziere die ganze Zahl mit dem Nenner und addiere den resultierenden Wert zum Zähler.
– Der Nenner bleibt unverändert.

Beispiel:
2 1/3 * 2/5
Umwandlung der gemischten Zahl 2 1/3 in einen Bruch:
Zähler: (2 * 3) + 1 = 7
Nenner: 3

Das Ergebnis ist also 7/3.

Bruchrechnung: Die richtige Methode zur Multiplikation von Brüchen

Einführung zur Multiplikation von Brüchen

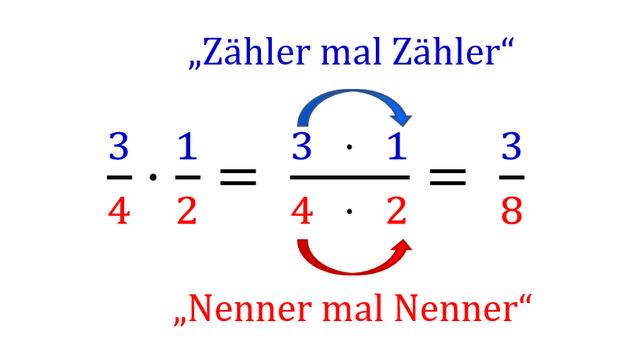
Beim Bruchrechnen ist die Multiplikation eine wichtige Operation. Um zwei Brüche zu multiplizieren, multipliziert man einfach den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs und den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs. Das Ergebnis ist dann der neue Bruch, bei dem der Zähler das Produkt der beiden Zähler ist und der Nenner das Produkt der beiden Nenner.

Beispiel für die Multiplikation von zwei Brüchen

Angenommen, wir möchten die beiden Brüche 1/7 und 2/3 multiplizieren. Zuerst multiplizieren wir den Zähler 1 des ersten Bruchs mit dem Zähler 2 des zweiten Bruchs: 1 * 2 = 2. Dann multiplizieren wir den Nenner 7 des ersten Bruchs mit dem Nenner 3 des zweiten Bruchs: 7 * 3 = 21. Das Ergebnis ist also der neue Bruch 2/21.

Multiplikation von gemischten Zahlen

Wenn wir gemischte Zahlen multiplizieren möchten, müssen wir sie zuerst in einen unechten (oder sogenannten „falschen“) Bruch umwandeln. Dazu multiplizieren wir die ganze Zahl mit dem Nenner und addieren den resultierenden Wert zum bisherigen Zähler. Der Nenner bleibt unverändert. Anschließend können wir wie gewohnt die beiden Brüche multiplizieren.

Kürzen von Brüchen

Um Brüche zu vereinfachen, können wir sie kürzen. Dazu müssen Zähler und Nenner einen gemeinsamen Teiler haben. Indem wir beide durch denselben Teiler teilen, erhalten wir den gekürzten Bruch. Es ist ratsam, bereits vor der Multiplikation zu kürzen, um mit kleineren Zahlen zu rechnen und das Ergebnis übersichtlicher zu gestalten.

Multiplikation von mehr als zwei Brüchen

Die Multiplikation von mehr als zwei Brüchen funktioniert auf die gleiche Weise wie bei zwei Brüchen. Man multipliziert einfach alle Zähler miteinander und alle Nenner miteinander. Anschließend kann man den resultierenden Bruch eventuell noch kürzen.

Das Verständnis und die richtige Anwendung der Multiplikation von Brüchen sind wichtige Grundlagen in der Mathematik. Durch Übung und Anwendung kannst du deine Fähigkeiten in diesem Bereich verbessern und komplexe Aufgaben lösen.

Praktische Tipps zum Multiplizieren von Brüchen

Tipp 1: Zähler mit Zähler und Nenner mit Nenner multiplizieren

Beim Multiplizieren von Brüchen ist es wichtig, den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs zu multiplizieren und den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs. Dadurch erhält man das Produkt der beiden Brüche.

Tipp 2: Ganze Zahlen in einen Bruch umwandeln

Wenn du einen Bruch mit einer ganzen Zahl multiplizierst, musst du die ganze Zahl zuerst in einen Bruch umwandeln. Dazu schreibst du die ganze Zahl als Zähler auf den Bruchstrich und setzt den Nenner auf 1.

Tipp 3: Gemischte Zahlen in einen Bruch umwandeln

Bei der Multiplikation von gemischten Zahlen musst du zuerst die gemischte Zahl in einen unechten Bruch umwandeln. Du multiplizierst die ganze Zahl mit dem Nenner und addierst den bisherigen Zähler dazu. Der Nenner bleibt unverändert.

Tipp 4: Kürzen von Brüchen

Um das Ergebnis eines Produkts von Brüchen zu vereinfachen, kannst du den Zähler und den Nenner kürzen. Dafür müssen beide Teile des Bruchs einen gemeinsamen Teiler haben. Durch das Kürzen wird der Bruch einfacher dargestellt.

Tipp 5: Mehrere Brüche multiplizieren

Wenn du mehr als zwei Brüche multiplizieren musst, multipliziere zuerst alle Zähler miteinander und anschließend alle Nenner miteinander. Streiche dann die gemeinsamen Zahlen im Zähler und Nenner.

Diese praktischen Tipps helfen dir dabei, das Multiplizieren von Brüchen zu verstehen und erfolgreich anzuwenden. Übe weiterhin mit verschiedenen Aufgaben, um deine Fähigkeiten zu verbessern.

Verständliche Erklärung: So funktioniert die Multiplikation von Brüchen

Die Grundregel der Multiplikation von Brüchen

Um zwei Brüche zu multiplizieren, multiplizierst du einfach den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs und den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs. Das Ergebnis ist dann der neue Bruch.

Beispiel:
1/4 * 2/3 = (1 * 2) / (4 * 3) = 2/12

Multiplikation von Brüchen mit ganzen Zahlen

Wenn du einen Bruch mit einer ganzen Zahl multiplizieren möchtest, musst du die ganze Zahl zuerst in einen Bruch umwandeln. Dazu schreibst du die ganze Zahl als Zähler auf den Bruchstrich und den Nenner setzt du auf 1. Anschließend kannst du wie gewohnt die Zähler und Nenner miteinander multiplizieren.

Beispiel:
3 * 1/4 = (3 * 1) / (1 * 4) = 3/4

Multiplikation von gemischten Zahlen

Bei der Multiplikation von gemischten Zahlen musst du zuerst die gemischte Zahl in einen unechten oder zusammengesetzten Bruch umwandeln. Dazu multiplizierst du die ganze Zahl mit dem Nenner des Bruchs und addierst den bisherigen Zähler dazu. Den Nenner lässt du unverändert. Anschließend kannst du wie gewohnt die Zähler und Nenner miteinander multiplizieren.

Beispiel:
2 1/3 * 2/5 = ((2 * 3) + 1) / (3 * 5) = 7/15

Kürzen von Brüchen

Du kannst Brüche vereinfachen, indem du den Zähler und den Nenner durch dieselbe Zahl teilst. Das Ergebnis ist dann ein gekürzter Bruch, der den gleichen Wert hat wie der Ausgangsbruch.

Beispiel:
4/8 kann gekürzt werden zu 1/2, da sowohl der Zähler als auch der Nenner durch 4 teilbar sind.

Beim Multiplizieren von Brüchen kannst du auch über Kreuz kürzen. Das bedeutet, dass du den Zähler eines Bruchs mit dem Nenner des anderen Bruchs kürzen kannst.

Beispiel:
2/3 * 6/8 = (2 * 6) / (3 * 8) = (12 / 24) kann gekürzt werden zu (1 / 2), da sowohl der Zähler als auch der Nenner durch 12 teilbar sind.

Übungsaufgaben zur Bruchmultiplikation: Teste dein Wissen!

Aufgabe 1:

Multipliziere die beiden Brüche 2/3 und 5/6 miteinander.

Lösung:
Um die Brüche zu multiplizieren, multiplizieren wir den Zähler des ersten Bruchs (2) mit dem Zähler des zweiten Bruchs (5) und den Nenner des ersten Bruchs (3) mit dem Nenner des zweiten Bruchs (6).

2/3 * 5/6 = (2 * 5)/(3 * 6) = 10/18

Da sowohl der Zähler als auch der Nenner durch 2 teilbar sind, können wir den Bruch kürzen.

10/18 = 5/9

Die Lösung lautet also 5/9.

Aufgabe 2:

Multipliziere den gemischten Bruch 1 1/4 mit dem Bruch 2/5.

Lösung:
Um den gemischten Bruch zu multiplizieren, wandeln wir ihn zuerst in einen unechten Bruch um. Dazu multiplizieren wir die ganze Zahl (1) mit dem Nenner des gemischten Bruchs (4) und addieren den Zähler des gemischten Bruchs (1).

1 + (1 * 4)/4 = 1 + 4/4 = 1 + 1 = 2

Der gemischte Bruch wird also zu einem unechten Bruch von 2.

Jetzt können wir die beiden Brüche wie gewohnt multiplizieren:

2 * 2/5 = (2 * 2)/(1 * 5) = 4/5

Die Lösung lautet also 4/5.

Aufgabe 3:

Multipliziere die Brüche 3/8, 4/5 und 2/3 miteinander.

Lösung:
Um die Brüche zu multiplizieren, multiplizieren wir alle Zähler miteinander und alle Nenner miteinander.

(3 * 4 * 2)/(8 * 5 * 3) = 24/120

Auch hier können wir den Bruch kürzen. Da sowohl der Zähler als auch der Nenner durch 24 teilbar sind, teilen wir beide durch diese Zahl.

24/120 = 1/5

Die Lösung lautet also 1/5.

Zusammenfassend lässt sich sagen, dass das Multiplizieren von Brüchen eine einfache Methode ist, um das Produkt zweier oder mehrerer Brüche zu erhalten. Man multipliziert einfach die Zähler und die Nenner der Brüche miteinander. Dabei ist es wichtig, die Ergebnisse zu kürzen und gegebenenfalls den gemischten Bruch in einen unechten Bruch umzuwandeln. Mit ein wenig Übung kann das Multiplizieren von Brüchen problemlos gemeistert werden.