In diesem Artikel erfährst du, wie du den Umfang eines Kreises berechnen kannst. Wir werden dir Schritt für Schritt erklären, welche Formel du dafür verwenden musst und wie du die benötigten Werte ermittelst. Egal ob für schulische Aufgaben oder im Alltag – mit unseren Tipps wirst du schnell und einfach den Umfang eines Kreises bestimmen können. Los geht’s!
Kreisumfang berechnen: Formeln und Beispiele
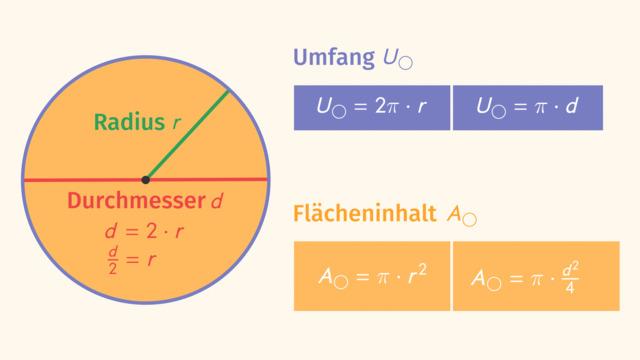
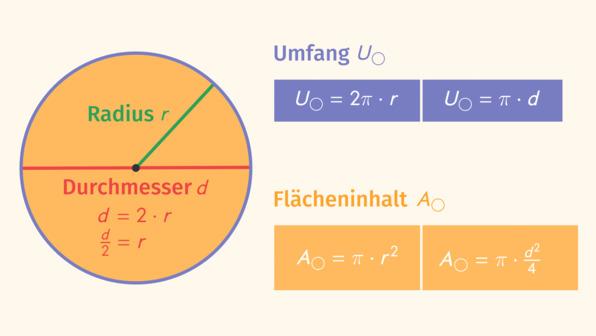
Ein Kreis ist eine runde geometrische Form, bei der jeder Punkt auf der Kreislinie den gleichen Abstand zum Mittelpunkt M hat. Der Umfang U eines Kreises ist die Länge der Kreislinie. Du kannst den Umfang eines Kreises mit Hilfe der Formel U = 2 · r · π oder U = d · π berechnen. Dabei benötigst du entweder den Radius r oder den Durchmesser d des Kreises.
Um den Umfang eines Kreises zu berechnen, musst du den Wert für den Radius oder den Durchmesser in die entsprechende Formel einsetzen und das Ergebnis bestimmen. Beachte dabei, dass der Durchmesser immer doppelt so lang ist wie der Radius (d = 2 · r).
Wenn du statt des Radius den Durchmesser eines Kreises gegeben hast, kannst du eine separate Formel verwenden. Setze einfach den Wert für den Durchmesser in die entsprechende Formel ein und rechne die Werte zusammen.
Manchmal möchtest du auch nur den Umfang eines Halbkreises berechnen. Hierbei musst du sowohl die Linie des Kreisbogens als auch die gerade Linie unten berücksichtigen, die dem Durchmesser entspricht. Die Berechnung erfolgt dann in mehreren Schritten.
Es ist auch möglich, den Umfang eines Kreises aus dem Flächeninhalt zu berechnen. Dafür gibt es eine spezielle Formel, bei der du die Wurzel aus dem Flächeninhalt ziehen musst.
Zusätzlich zu diesen Informationen über das Berechnen des Kreisumfangs gibt es auch Videos, in denen weitere Formeln und Beispiele erklärt werden. Du kannst dir diese Videos anschauen, um dein Wissen zu vertiefen.
Abschließend solltest du die Begriffe Passante, Sekante und Tangente kennen. Eine Passante schneidet den Kreis an keinem Punkt, eine Sekante schneidet den Kreis an genau zwei Punkten und eine Tangente schneidet den Kreis an genau einem Punkt.
Zusammenfassend hast du nun gelernt, wie du den Umfang eines Kreises berechnen kannst. Es gibt verschiedene Formeln für unterschiedliche Gegebenheiten wie Radius oder Durchmesser. Mit Hilfe dieser Formeln und einigen Beispielen kannst du den Umfang eines Kreises problemlos bestimmen.
Schritt-für-Schritt-Anleitung: Wie berechnet man den Umfang eines Kreises?
Schritt 1:
Um den Umfang eines Kreises zu berechnen, benötigst du entweder den Radius (r) oder den Durchmesser (d). Der Radius ist der Abstand von einem Punkt auf der Kreislinie zum Mittelpunkt des Kreises. Der Durchmesser verbindet zwei Punkte auf der Kreislinie und geht immer durch den Mittelpunkt.
Schritt 2:
Wenn du den Radius hast, kannst du die Formel U = 2 · r · π verwenden, um den Umfang zu berechnen. Setze einfach den Wert für den Radius in die Formel ein und berechne das Ergebnis.
Wenn du stattdessen den Durchmesser hast, verwendest du die Formel U = d · π. Beachte dabei, dass der Durchmesser immer doppelt so lang ist wie der Radius (d = 2 · r).
Schritt 3:
Falls dir weder der Radius noch der Durchmesser gegeben sind, kannst du auch den Flächeninhalt des Kreises verwenden, um den Umfang zu berechnen. Die Formel für den Flächeninhalt eines Kreises lautet A = π · r^2 oder A = (π · d^2) / 4.
Löse diese Formel nach dem Radius oder dem Durchmesser auf und setze dann den entsprechenden Wert in die Umfangsformel ein.
Zusammenfassung:
Um den Umfang eines Kreises zu berechnen:
– Wenn der Radius gegeben ist: U = 2 · r · π
– Wenn der Durchmesser gegeben ist: U = d · π (d = 2 · r)
– Wenn der Flächeninhalt gegeben ist: Berechne den Radius oder den Durchmesser aus der Flächenformel und setze ihn in die Umfangsformel ein.
Denke daran, dass die Kreiszahl π ≈ 3,1415 ist und du sie entweder als genauen Wert oder gerundet verwenden kannst.
Umfang eines Kreises ermitteln: Radius oder Durchmesser verwenden
Einleitung
Ein Kreis ist eine runde geometrische Form, bei der jeder Punkt auf der Kreislinie den gleichen Abstand zum Mittelpunkt hat. Der Umfang eines Kreises ist die Länge der Kreislinie und kann mit verschiedenen Formeln berechnet werden.
Berechnung mit dem Radius
Um den Umfang eines Kreises zu berechnen, benötigt man entweder den Radius oder den Durchmesser. Der Radius ist der Abstand von einem Punkt auf der Kreislinie zum Mittelpunkt. Mit der Formel U = 2 · r · π oder U = d · π kann man den Umfang berechnen, wobei π die Kreiszahl Pi (ungefähr 3,1415) ist.
Beispiel:
Gegeben sei ein Kreis mit einem Radius von 5 cm.
U = 2 · 5 cm · π
U = 10 cm · π
U ≈ 31,4159 cm
Berechnung mit dem Durchmesser
Alternativ kann auch der Durchmesser des Kreises verwendet werden. Der Durchmesser verbindet einen Punkt auf der Kreislinie mit dem gegenüberliegenden Punkt und geht immer durch den Mittelpunkt. Da der Durchmesser d genau doppelt so lang wie der Radius r ist (d = 2 · r), kann man eine andere Formel für den Umfang verwenden: U = d · π.
Beispiel:
Gegeben sei ein Kreis mit einem Durchmesser von 10 m.
U = 10 m · π
U ≈ 31,4159 m
Berechnung des Umfangs eines Halbkreises
Für die Berechnung des Umfangs eines Halbkreises verwendet man sowohl den Kreisbogen als auch die gerade Linie unten, die dem Durchmesser entspricht. Der Umfang wird daher in mehreren Schritten berechnet.
Beispiel:
Gegeben sei ein Halbkreis mit einem Durchmesser von 5 cm.
Zuerst wird der gesamte Kreisumfang berechnet: U = 2 · r · π = 2 · (5 cm / 2) · π ≈ 15,7079 cm
Dann wird der Umfang des Halbkreises ermittelt, indem der Kreisbogen mit dem Durchmesser zusammengezählt wird: U = (15,7079 cm / 2) + 5 cm ≈ 12,8539 cm
Berechnung des Umfangs aus dem Flächeninhalt
Es ist auch möglich, den Umfang eines Kreises aus dem Flächeninhalt zu berechnen. Dafür verwendet man die Formel A = π · r^2 oder A = (π · d^2) : 4. Indem man die Formel nach dem Radius auflöst und den gegebenen Flächeninhalt einsetzt, kann man den Radius bestimmen und anschließend den Umfang berechnen.
Beispiel:
Gegeben sei eine Kreisfläche von 25 cm^2.
A = π · r^2
25 cm^2 = π · r^2
r^2 = 25 cm^2 / π
r ≈ √(25 cm^2 / π)
r ≈ √(7,9577 cm)
r ≈ 2,8214 cm
U = 2 · r · π
U = 2 · 2,8214 cm · π
U ≈ 17,7715 cm
Zusammenfassung
Du hast jetzt gelernt, wie man den Umfang eines Kreises berechnet, indem man entweder den Radius oder den Durchmesser verwendet. Du kennst auch die Begriffe Passante, Sekante und Tangente in Bezug auf Geraden am Kreis. Weitere Formeln für den Kreis sind die Berechnung des Flächeninhalts und des Durchmessers.
Berechnung des Kreisumfangs mit Hilfe der Pi-Zahl
Der Umfang eines Kreises kann mithilfe der Pi-Zahl berechnet werden. Dabei gibt es zwei Formeln, die verwendet werden können: U = 2 · r · π oder U = d · π. Hierbei steht U für den Umfang, r für den Radius und d für den Durchmesser des Kreises.
Um den Umfang zu berechnen, benötigt man entweder den Radius oder den Durchmesser. Der Radius ist der Abstand von einem Punkt auf der Kreislinie zum Mittelpunkt M, während der Durchmesser eine Strecke im Kreis ist, die genau doppelt so lang wie der Radius ist.
Die Pi-Zahl (π) hat einen ungefähren Wert von 3,1415 und ist in vielen Taschenrechnern bereits gespeichert. Alternativ kann auch ein gerundeter Wert verwendet werden.
Um den Umfang eines Halbkreises zu berechnen, müssen sowohl die Linie des Kreisbogens als auch die gerade Linie unten berücksichtigt werden, welche dem Durchmesser entspricht. Daher wird hierbei nicht nur eine Formel verwendet, sondern mehrere Schritte sind erforderlich.
Es besteht auch die Möglichkeit, den Umfang eines Kreises aus dem Flächeninhalt zu berechnen. Hierbei muss jedoch beachtet werden, dass Längen immer als positive Zahlen angegeben werden und daher nur der positive Wert aus der Wurzel verwendet wird.
Zusätzlich zu diesen Informationen gibt es noch weitere Formeln und Begriffe im Zusammenhang mit einem Kreis wie Passante, Sekante und Tangente. Diese können genutzt werden, um weitere Berechnungen durchzuführen.
Abschließend kann der Umfang eines Kreises berechnet werden, indem die entsprechenden Werte in die Formel eingesetzt und das Ergebnis ermittelt wird. Es ist auch möglich, den Umfang eines Halbkreises oder den Flächeninhalt eines Kreises zu berechnen, indem verschiedene Schritte durchgeführt werden.
Umfang eines Halbkreises bestimmen: Schritte und Formeln
Schritt 1:
Zuerst bestimmst du den gesamten Umfang des Kreises mit der Formel U = 2 · r · π oder U = d · π.
Schritt 2:
Teile den berechneten Umfang des Kreises durch 2, um die Länge des Halbkreisbogens zu erhalten.
Schritt 3:
Addiere die Länge des Halbkreisbogens mit der Länge der geraden Linie unten, die dem Durchmesser entspricht. So erhältst du den Umfang des Halbkreises.
Formeln:
– Gesamtumfang eines Kreises: U = 2 · r · π oder U = d · π
– Länge des Halbkreisbogens: (U vom gesamten Kreis) / 2
– Umfang eines Halbkreises: (Länge des Halbkreisbogens) + (Länge der geraden Linie unten)
Beispiel:
Angenommen, wir haben einen Halbkreis mit einem Durchmesser von 5 cm.
Schritt 1:
Der gesamte Umfang des Kreises beträgt U = (5 cm) · π ≈ 15,71 cm.
Schritt 2:
Die Länge des Halbkreisbogens beträgt (15,71 cm) / 2 ≈ 7,86 cm.
Schritt 3:
Der Umfang des Halbkreises beträgt (7,86 cm) + (5 cm) ≈ 12,86 cm.
Auf diese Weise kannst du den Umfang eines Halbkreises berechnen, indem du die Formeln und Schritte befolgst.
Kreisumfang aus Flächeninhalt ableiten: Beispiel und Vorgehensweise
Um den Kreisumfang aus dem Flächeninhalt abzuleiten, müssen wir eine bestimmte Formel verwenden. Hier ist ein Beispiel und die Vorgehensweise:
Beispiel:
Gegeben ist der Flächeninhalt eines Kreises mit A = 25 cm². Gesucht ist der Umfang des Kreises.
Vorgehensweise:
1. Schreibe die Formel für den Flächeninhalt eines Kreises auf: A = π · r²
2. Löse die Formel nach dem Radius r auf: r = √(A/π)
3. Setze den gegebenen Wert für den Flächeninhalt ein: r = √(25 cm²/π)
4. Berechne den Wert für den Radius: r ≈ √(7,96 cm) ≈ 2,82 cm
5. Verwende nun die Formel für den Umfang des Kreises: U = 2 · π · r
6. Setze den berechneten Wert für den Radius ein: U ≈ 2 · π · 2,82 cm ≈ 17,75 cm
Der Umfang des Kreises beträgt also ungefähr 17,75 cm.
Das war die Vorgehensweise, um den Kreisumfang aus dem Flächeninhalt abzuleiten.
Insgesamt ist die Berechnung des Umfangs eines Kreises eine einfache und wichtige mathematische Aufgabe. Mit der Formel 2 * π * r kann der Umfang schnell und genau ermittelt werden. Es ist jedoch wichtig, den Radius korrekt zu messen, um genaue Ergebnisse zu erhalten. Die Kenntnis des Umfangs eines Kreises ist nützlich in verschiedenen Bereichen wie Geometrie, Architektur und Technik.

