Effizienter Flächeninhalt berechnen: Tipps und Tricks!

„Der Flächeninhalt ist eine wichtige Berechnung in der Geometrie. In diesem Artikel erfährst du, wie du den Flächeninhalt von verschiedenen Formen berechnen kannst. Erfahre die grundlegenden Formeln und praktische Beispiele, um dein mathematisches Verständnis zu verbessern.“

Schritt-für-Schritt-Anleitung zur Berechnung des Flächeninhalts

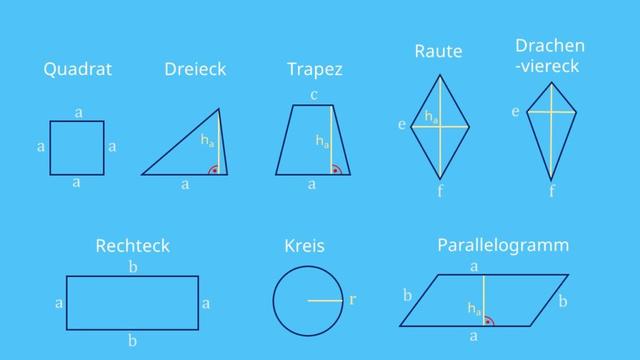
1. Grundlagen verstehen

Bevor man den Flächeninhalt einer Form berechnen kann, ist es wichtig, die Grundlagen zu verstehen. Der Flächeninhalt gibt an, wie groß eine Fläche ist und wird in Quadratmetern (m²) oder Quadratzentimetern (cm²) gemessen. Um den Flächeninhalt zu berechnen, muss man die richtige Formel verwenden, abhängig von der Art der Fläche.

2. Messungen durchführen

Um den Flächeninhalt einer geometrischen Figur zu berechnen, müssen zunächst Messungen durchgeführt werden. Je nach Form können verschiedene Maße benötigt werden, wie beispielsweise Länge, Breite oder Radius. Es ist wichtig, genaue und korrekte Messungen durchzuführen, um ein präzises Ergebnis zu erhalten.

3. Richtige Formel anwenden

Nachdem alle erforderlichen Messungen vorgenommen wurden, kann die richtige Formel angewendet werden, um den Flächeninhalt zu berechnen. Je nach Art der Figur gibt es unterschiedliche Formeln. Zum Beispiel wird für ein Rechteck der Flächeninhalt durch Multiplikation von Länge und Breite berechnet: A = Länge * Breite. Für einen Kreis wird die Formel A = π * Radius^2 verwendet.

Es ist wichtig sicherzustellen, dass die richtige Einheit verwendet wird und alle Berechnungen korrekt durchgeführt werden, um ein genaues Ergebnis für den Flächeninhalt zu erhalten.

Methoden zur Ermittlung des Flächeninhalts erklärt

1. Methode: Rechteckige Flächen

Eine der einfachsten Methoden, um den Flächeninhalt zu berechnen, ist für rechteckige Formen. Der Flächeninhalt eines Rechtecks kann durch Multiplikation der Länge mit der Breite berechnet werden. Zum Beispiel hat ein Rechteck mit einer Länge von 5 cm und einer Breite von 3 cm einen Flächeninhalt von 15 cm².

2. Methode: Dreieckige Flächen

Die Berechnung des Flächeninhalts eines Dreiecks erfordert eine etwas andere Methode. Hierbei wird die Formel „Grundseite mal Höhe geteilt durch 2“ verwendet. Die Grundseite ist die längste Seite des Dreiecks, auf der das Dreieck steht, und die Höhe ist die senkrechte Linie, die von der Spitze des Dreiecks bis zur Grundseite verläuft. Wenn zum Beispiel die Grundseite eines Dreiecks 8 cm lang ist und die Höhe 6 cm beträgt, dann beträgt der Flächeninhalt des Dreiecks (8 cm * 6 cm) / 2 = 24 cm².

3. Methode: Kreisfläche

Die Berechnung des Flächeninhalts eines Kreises erfordert eine spezielle Formel. Der Flächeninhalt eines Kreises kann mit dem Radius berechnet werden, indem man den Radius quadriert und mit Pi multipliziert (Flächeninhalt = r² * Pi). Zum Beispiel hat ein Kreis mit einem Radius von 5 cm einen Flächeninhalt von 25 cm² * Pi ≈ 78,54 cm².

Es gibt noch viele weitere Methoden zur Berechnung des Flächeninhalts, je nach Form und Geometrie der Fläche. Diese drei Methoden sind jedoch grundlegende und häufig verwendete Ansätze, um den Flächeninhalt zu ermitteln.

Wie man den Flächeninhalt richtig berechnet

1. Berechnung des Flächeninhalts eines Rechtecks

Um den Flächeninhalt eines Rechtecks zu berechnen, multipliziert man einfach die Länge der einen Seite mit der Länge der anderen Seite. Die Formel lautet: Flächeninhalt = Länge * Breite. Zum Beispiel, wenn ein Rechteck eine Länge von 5 Metern und eine Breite von 3 Metern hat, beträgt der Flächeninhalt 15 Quadratmeter.

2. Berechnung des Flächeninhalts eines Dreiecks

Um den Flächeninhalt eines Dreiecks zu berechnen, kann man die Formel „Grundseite * Höhe / 2“ verwenden. Die Grundseite ist dabei eine der Seiten des Dreiecks und die Höhe ist die senkrechte Linie, die von dieser Seite zur gegenüberliegenden Ecke gezogen wird. Man multipliziert also die Grundseite mit der Höhe und teilt das Ergebnis durch 2. Zum Beispiel, wenn ein Dreieck eine Grundseite von 6 Metern und eine Höhe von 4 Metern hat, beträgt der Flächeninhalt 12 Quadratmeter.

3. Berechnung des Flächeninhalts eines Kreises

Der Flächeninhalt eines Kreises kann mit Hilfe der Formel „π * Radius^2“ berechnet werden. Dabei steht π für Pi (ungefähr 3,14159) und der Radius ist der Abstand vom Mittelpunkt des Kreises bis zu einem Punkt auf dem Rand. Man quadriert also den Radius und multipliziert das Ergebnis mit Pi. Zum Beispiel, wenn ein Kreis einen Radius von 5 Metern hat, beträgt der Flächeninhalt etwa 78,54 Quadratmeter.

Es gibt natürlich noch viele weitere Formeln und Methoden, um den Flächeninhalt verschiedener geometrischer Figuren zu berechnen. Diese drei Beispiele sollen jedoch einen guten Einstieg bieten und die grundlegenden Prinzipien verdeutlichen.

Formeln und Vorgehensweisen zur Flächenberechnung

Flächenformeln für einfache geometrische Figuren

Die Berechnung des Flächeninhalts verschiedener geometrischer Figuren erfordert das Anwenden spezifischer Formeln. Für einfache Figuren wie Rechtecke, Quadrate und Dreiecke gibt es bekannte Flächenformeln. Zum Beispiel berechnet sich der Flächeninhalt eines Rechtecks durch das Produkt von Länge und Breite: A = Länge * Breite. Bei einem Quadrat mit Seitenlänge a ergibt sich die Fläche einfach durch A = a^2. Für ein Dreieck kann die Formel A = (Grundseite * Höhe) / 2 verwendet werden.

Vorgehensweise bei komplexen Figuren

Bei komplexeren Figuren, wie beispielsweise Kreisen oder unregelmäßigen Vierecken, gestaltet sich die Berechnung des Flächeninhalts etwas schwieriger. Hier ist es hilfreich, die Figur in kleinere Teilfiguren zu zerlegen, für die bereits bekannte Formeln existieren. Anschließend können die einzelnen Flächen addiert werden, um den Gesamtflächeninhalt zu erhalten.

Eine weitere Methode zur Berechnung des Flächeninhalts einer unregelmäßigen Figur ist das Verwenden von Gitternetzen. Indem man ein Gitternetz über die Figur legt und dann zählt, wie viele volle Kästchen innerhalb der Figur liegen und wie viele halbe Kästchen an den Rändern, kann man eine Annäherung des Flächeninhalts erhalten.

Es ist wichtig, die richtige Einheit für den Flächeninhalt zu verwenden. In der Regel wird der Flächeninhalt in Quadratmetern (m²) angegeben, aber je nach Kontext können auch andere Einheiten wie Quadratzentimeter (cm²) oder Quadratkilometer (km²) verwendet werden.

Praktische Tipps für die Berechnung des Flächeninhalts

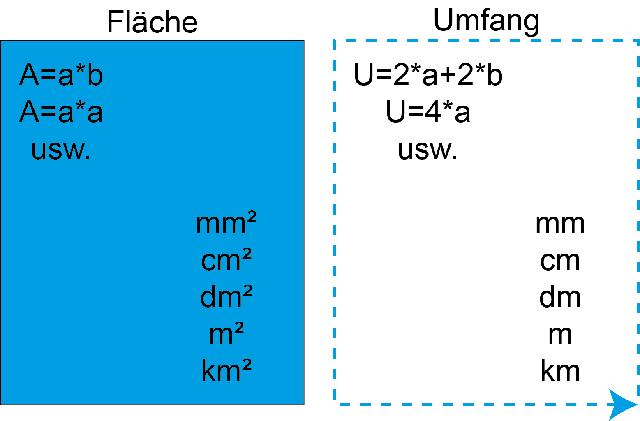
1. Verwende die richtige Formel

Um den Flächeninhalt einer bestimmten Figur zu berechnen, ist es wichtig, die richtige Formel zu verwenden. Jede Figur hat ihre eigene spezifische Formel zur Berechnung des Flächeninhalts. Zum Beispiel kann der Flächeninhalt eines Rechtecks durch die Länge mal Breite berechnet werden, während der Flächeninhalt eines Kreises durch den Radius im Quadrat mal Pi berechnet wird. Stelle sicher, dass du die entsprechende Formel verwendest, um genaue Ergebnisse zu erhalten.

2. Zerlege komplexe Figuren in einfachere Teile

Manchmal kann es schwierig sein, den Flächeninhalt einer komplexen Figur direkt zu berechnen. In solchen Fällen kann es hilfreich sein, die Figur in einfachere Teile zu zerlegen und dann den Flächeninhalt jedes einzelnen Teils zu berechnen. Addiere anschließend alle Teilflächen zusammen, um den Gesamtflächeninhalt der komplexen Figur zu erhalten.

3. Achte auf Einheiten und Genauigkeit

Bei der Berechnung des Flächeninhalts ist es wichtig, auf die Einheiten und Genauigkeit zu achten. Stelle sicher, dass alle Maßeinheiten einheitlich sind (z.B. Meter oder Zentimeter) und konvertiere sie gegebenenfalls in eine gemeinsame Einheit. Außerdem solltest du bei deinen Berechnungen eine angemessene Genauigkeit beibehalten, um genauere Ergebnisse zu erzielen.

Diese praktischen Tipps können dir dabei helfen, den Flächeninhalt von verschiedenen Figuren korrekt zu berechnen. Indem du die richtige Formel verwendest, komplexe Figuren in einfachere Teile zerlegst und auf Einheiten und Genauigkeit achtest, kannst du genaue Ergebnisse erzielen und mathematische Probleme effektiv lösen.

Die wichtigsten Schritte zur Bestimmung des Flächeninhalts

1. Bestimmen der Form und Abmessungen der Fläche

Um den Flächeninhalt einer Figur zu berechnen, ist es zunächst wichtig, die Form und die Abmessungen der Fläche zu bestimmen. Je nachdem, um welche Art von Figur es sich handelt, gibt es unterschiedliche Formeln zur Berechnung des Flächeninhalts. Beispielsweise hat ein Rechteck einen anderen Berechnungsansatz als ein Dreieck oder ein Kreis.

2. Anwenden der entsprechenden Formel

Sobald die Form und die Abmessungen der Fläche bekannt sind, kann die entsprechende Formel zur Berechnung des Flächeninhalts angewendet werden. Für einfache geometrische Figuren wie Rechtecke oder Quadrate ist dies relativ einfach, da es dafür bekannte Formeln gibt. Bei komplexeren Figuren wie Trapezen oder Kreisen müssen spezifischere Formeln verwendet werden.

3. Einsetzen der Werte und Berechnen des Ergebnisses

Nachdem die richtige Formel ausgewählt wurde, müssen die bekannten Werte für Länge, Breite, Radius oder andere Abmessungen in die entsprechenden Variablen eingesetzt werden. Anschließend kann mit Hilfe von mathematischen Operationen der Flächeninhalt berechnet werden. Es ist wichtig sicherzustellen, dass alle Einheiten einheitlich sind (z.B. Meter oder Quadratmeter), um korrekte Ergebnisse zu erhalten.

Zusammenfassend sind dies die drei wichtigsten Schritte zur Bestimmung des Flächeninhalts einer Figur. Indem man die Form und Abmessungen der Fläche bestimmt, die richtige Formel anwendet und die Werte einsetzt, kann der Flächeninhalt berechnet werden. Es ist ratsam, sich mit den verschiedenen Formeln für unterschiedliche Figuren vertraut zu machen, um in der Lage zu sein, den Flächeninhalt effektiv zu berechnen.

Zusammenfassend lässt sich sagen, dass der Flächeninhalt einer geometrischen Figur durch unterschiedliche Formeln berechnet werden kann. Die Art der Figur bestimmt die jeweilige Formel, die angewendet werden muss. Es ist wichtig, die richtige Formel zu verwenden, um genaue Ergebnisse zu erzielen. Durch das Verständnis und die Anwendung dieser Berechnungsmethoden können wir den Flächeninhalt verschiedener Figuren problemlos bestimmen.