Prismen sind geometrische Körper mit einer besonderen Form, die oft in der Optik und Physik verwendet werden. Sie bestehen aus einem Material mit unterschiedlichem Brechungsindex, was dazu führt, dass Lichtstrahlen beim Durchgang durch den Prismenkörper gebrochen oder reflektiert werden. Diese Eigenschaften ermöglichen es Prismen, Licht zu brechen und zu streuen, wodurch sie in vielen Anwendungen wie Spektroskopie und Bildgebung unverzichtbar sind. Lernen Sie mehr über die faszinierenden Eigenschaften und Anwendungen von Prismen!
Alles über Prismen: Eigenschaften und Anwendungen
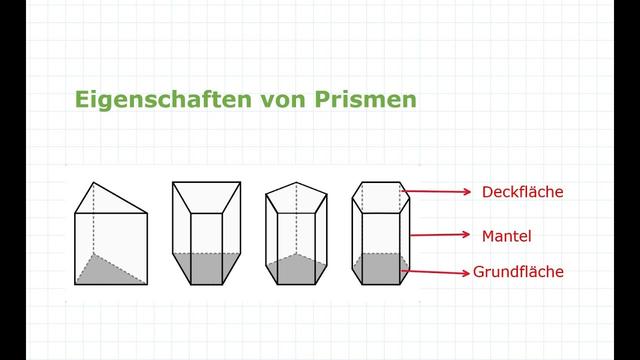
Prismen sind dreidimensionale Körper, die aus einer Grundfläche, einer Deckfläche und einer Mantelfläche bestehen. Die Grundfläche und die Deckfläche liegen parallel zueinander und haben dieselbe Form. Diese Form kann bei jedem Prisma unterschiedlich sein, muss aber mindestens drei Ecken haben. Ein klassisches Beispiel ist ein dreieckiges Prisma oder ein sechseckiges Prisma.
Prismen begegnen uns nicht nur in der Mathematik, sondern auch im Alltag als Gegenstände. Zum Beispiel ist das Dach vieler Häuser ein liegendes dreieckiges Prisma. In der Physik spielen Prismen eine wichtige Rolle bei der Lichtbrechung.
Um ein Prisma in der Geometrie zu erkennen, muss man wissen, dass es sich um eine spezielle Gruppe von Körpern handelt. Die Grundfläche kann unterschiedlich viele Ecken haben. Das bekannteste ist das dreieckige Prisma, aber auch Prismen mit anderen Vielecken als Grundfläche gehören zu dieser Gruppe.
Die Mantelfläche eines Prismas besteht immer aus mehreren Rechtecken, unabhängig von der Form der Grundfläche. Quader und Würfel können ebenfalls als eine besondere Art von Prismen betrachtet werden, da ihre Grundfläche ein Viereck ist.
Um den Flächeninhalt der Mantelfläche eines Prismas zu berechnen, multipliziert man den Umfang der Grundfläche mit der Höhe des Prismas.
Das Volumen eines Prismas wird berechnet, indem man den Flächeninhalt der Grundfläche mit der Höhe des Prismas multipliziert.
Der Oberflächeninhalt eines Prismas setzt sich aus der Grundfläche, der Deckfläche und der Mantelfläche zusammen. Man berechnet den Flächeninhalt dieser drei Teile und addiert sie.
Es gibt auch schräge Prismen, bei denen die Kanten nicht senkrecht auf der Grundfläche stehen. In diesem Fall liegt die Höhe außerhalb des Prismas.
Prismen sind in verschiedenen Anwendungen wichtig, sowohl in der Mathematik als auch in anderen Bereichen wie Architektur oder Physik.
Grundlagen zu Prismen: Formen, Mantelfläche und mehr
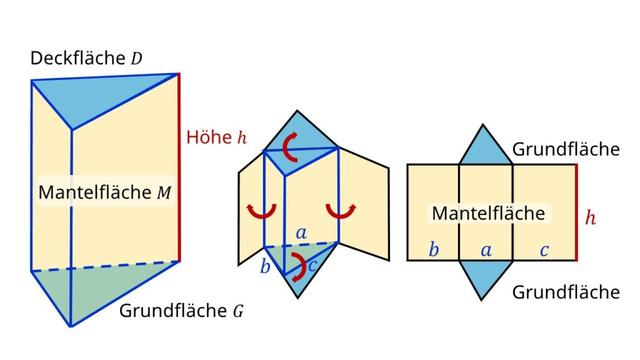
Ein Prisma ist ein dreidimensionaler Körper, der aus einer Grundfläche, einer Deckfläche und einer Mantelfläche besteht. Die Grundfläche und die Deckfläche sind parallel zueinander und haben dieselbe Form, die bei jedem Prisma unterschiedlich sein kann. Sie muss jedoch mindestens drei Ecken haben.
In der Geometrie bezeichnet man mit „Prismen“ nicht nur einen ganz speziellen Körper, sondern gleich eine ganze Gruppe von Körpern. Diese Gruppe umfasst Prismen mit unterschiedlich vielen Ecken auf der Grundfläche. Das bekannteste Prisma ist das dreieckige Prisma, aber auch Prismen mit anderen Vielecken als Grundfläche gehören dazu.
Die Mantelfläche eines Prismas besteht immer aus Rechtecken, unabhängig von der Form der Grundfläche. Quader und Würfel können ebenfalls als eine besondere Art von Prismen betrachtet werden, da sie als Grundfläche ein Viereck haben.
Eigenschaften eines Prismas:
- Dreidimensionaler Körper
- Besteht aus einer Grundfläche, einer Deckfläche und einer Mantelfläche
- Grund- und Deckfläche liegen parallel zueinander und haben dieselbe Form
- Grundfläche hat mindestens drei Ecken
- Mantelfläche besteht aus Rechtecken
Berechnung des Flächeninhalts der Mantelfläche:
Um die Mantelfläche eines Prismas zu berechnen, multipliziert man den Umfang der Grundfläche mit der Höhe des Prismas. Der Umfang der Grundfläche ergibt sich aus der Addition der Längen aller Kanten.
Berechnung des Volumens:
Das Volumen eines Prismas erhält man, indem man den Flächeninhalt der Grundfläche mit der Höhe des Prismas multipliziert.
Berechnung des Oberflächeninhalts:
Der Oberflächeninhalt eines Prismas setzt sich aus dem Flächeninhalt der Grundfläche, dem Flächeninhalt der Deckfläche und dem Flächeninhalt der Mantelfläche zusammen. Die Formel lautet: Oberflächeninhalt = 2 * (Flächeninhalt Grundfläche) + (Flächeninhalt Mantelfläche).
Es gibt auch schräge Prismen, bei denen die Kanten nicht senkrecht auf der Grundfläche stehen und die Höhe außerhalb des Prismas liegt.
Prisma in der Geometrie: Erkennungsmerkmale und Berechnungen
Ein Prisma ist ein dreidimensionaler Körper, der aus einer Grundfläche, einer Deckfläche und einer Mantelfläche besteht. Die Grundfläche und die Deckfläche liegen parallel zueinander und haben dieselbe Form. Diese Form kann bei jedem Prisma unterschiedlich sein, muss aber mindestens drei Ecken haben. Ein klassisches Beispiel für ein Prisma ist ein dreieckiges Prisma oder ein sechseckiges Prisma.
Prismen begegnen uns nicht nur in der Mathematik, sondern auch im Alltag als Gegenstände. Das Dach vieler Häuser zum Beispiel ist ein liegendes dreieckiges Prisma. In der Physik spielen Prismen eine besonders wichtige Rolle bei der Lichtbrechung.
Um ein Prisma in der Geometrie zu erkennen, musst du wissen, dass es sich um einen geometrischen Körper handelt. Andere dreidimensionale Körper, die dir vielleicht schon bekannt sind, sind die Kugel, der Zylinder oder der Quader. Allerdings bezeichnet man mit „Prismen“ in der Geometrie nicht nur einen speziellen Körper, sondern eine ganze Gruppe von Körpern. Die Grundfläche kann nämlich unterschiedlich viele Ecken haben. Das bekannteste ist das dreieckige Prisma, aber auch Prismen mit anderen Vielecken als Grundfläche gehören zu dieser Gruppe.
Alle Prismen haben gemeinsam, dass ihre Mantelfläche aus Rechtecken besteht – unabhängig von der Form der Grundfläche. Übrigens kannst du den Quader und den Würfel auch als eine besondere Art von Prismen betrachten, da ihre Grundfläche ein Viereck ist.
Um die Mantelfläche eines Prismas zu berechnen, multiplizierst du den Umfang der Grundfläche mit der Höhe des Prismas. Der Umfang der Grundfläche ergibt sich einfach durch die Addition der Längen aller Kanten. Als Höhe des Prismas verwendest du die Länge einer Kante, die die Grund- und Deckfläche verbindet.
Das Volumen eines Prismas berechnest du, indem du den Flächeninhalt der Grundfläche mit der Höhe des Prismas multiplizierst. Der Oberflächeninhalt setzt sich aus dem Flächeninhalt der Grundfläche, dem Flächeninhalt der Deckfläche und dem Flächeninhalt der Mantelfläche zusammen.
Es gibt auch schräge Prismen, bei denen die Kanten nicht senkrecht auf der Grundfläche stehen. Hier musst du bei der Berechnung auch aufpassen, da die Höhe außerhalb des Prismas liegt.
Jetzt bist du bestens vorbereitet, um Prismen in der Geometrie zu erkennen und alle wichtigen Größen eines Prisma zu berechnen!
Prismen in der Physik: Bedeutung bei der Lichtbrechung
Prismen spielen eine wichtige Rolle bei der Lichtbrechung in der Physik. Wenn Licht auf eine Prismenoberfläche trifft, wird es gebrochen und in verschiedene Farben aufgespalten. Dieser Effekt ist bekannt als Dispersion. Das liegt daran, dass das Licht beim Übergang von einem Medium zum anderen seine Richtung ändert und sich dadurch die verschiedenen Farben des Lichtspektrums voneinander trennen.
Ein bekanntes Beispiel für die Anwendung von Prismen bei der Lichtbrechung ist das Prisma im Regenbogen. Wenn Sonnenlicht durch Regentropfen fällt, wird es von den Wassertropfen gebrochen und in seine verschiedenen Farben aufgeteilt. Dadurch entsteht der beeindruckende Anblick eines Regenbogens.
In der Optik werden Prismen auch verwendet, um Lichtstrahlen zu lenken oder zu korrigieren. Zum Beispiel werden sie in Kameralinsen oder Ferngläsern eingesetzt, um das einfallende Licht so zu brechen, dass ein scharfes Bild entsteht.
Prismen haben also nicht nur in der Geometrie, sondern auch in der Physik eine große Bedeutung bei der Untersuchung und Manipulation von Licht. Sie ermöglichen uns, die Eigenschaften des Lichts besser zu verstehen und haben zahlreiche praktische Anwendungen in verschiedenen Bereichen wie Optik, Fotografie und Astronomie.
Volumen und Oberflächeninhalt von Prismen berechnen
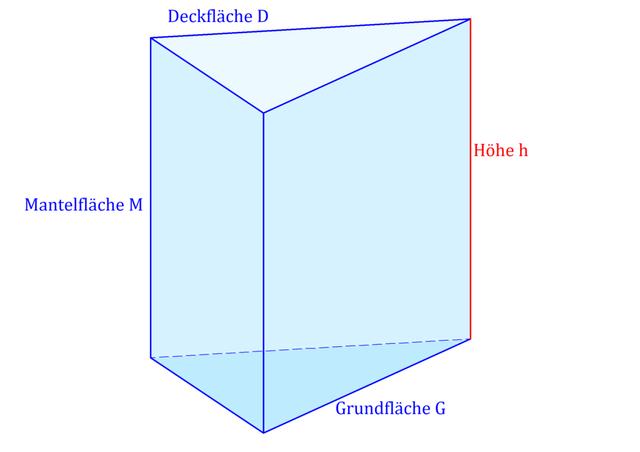
Ein Prisma ist ein dreidimensionaler Körper, der aus einer Grundfläche, einer Deckfläche und einer Mantelfläche besteht. Die Grundfläche und die Deckfläche liegen parallel zueinander und haben dieselbe Form. Diese Form kann bei jedem Prisma unterschiedlich sein, muss aber mindestens drei Ecken haben. Beispiele für Prismen mit verschiedenen Grundflächen sind das dreieckige Prisma oder das sechseckige Prisma.
Prismen begegnen uns nicht nur in der Mathematik, sondern auch im Alltag. Ein bekanntes Beispiel ist das Dach vieler Häuser, welches ein liegendes dreieckiges Prisma darstellt. In der Physik spielen Prismen eine besonders wichtige Rolle bei der Lichtbrechung.
Um ein Prisma in der Geometrie zu erkennen, muss es bestimmte Eigenschaften aufweisen. Es handelt sich um einen geometrischen Körper, der zu einer Gruppe von Körpern gehört. Diese Gruppe umfasst verschiedene Prismen mit unterschiedlichen Anzahlen von Ecken auf der Grundfläche. Die Mantelfläche eines Prismas besteht immer aus mehreren Rechtecken, unabhängig von der Form der Grundfläche.
Quader und Würfel können ebenfalls als spezielle Arten von Prismen betrachtet werden, da ihre Grundfläche ein Viereck ist.
Um den Flächeninhalt der Mantelfläche eines Prismas zu berechnen, multipliziert man den Umfang der Grundfläche mit der Höhe des Prismas. Der Umfang der Grundfläche ergibt sich durch die Addition aller Kantenlängen der Grundfläche.
Das Volumen eines Prismas berechnet man, indem man den Flächeninhalt der Grundfläche mit der Höhe des Prismas multipliziert. Die Höhe entspricht dabei der Länge einer Kante, die die Grund- und Deckfläche verbindet.
Der Oberflächeninhalt eines Prismas setzt sich aus dem Flächeninhalt der Grundfläche, dem Flächeninhalt der Deckfläche und dem Flächeninhalt der Mantelfläche zusammen. Da die Grund- und Deckfläche deckungsgleich sind, haben sie den gleichen Flächeninhalt. Der Oberflächeninhalt ergibt sich also durch die Addition dieser drei Teilflächen.
Es gibt auch schräge Prismen in der Geometrie, bei denen die Kanten nicht senkrecht auf der Grundfläche stehen. Hier muss man bei der Berechnung des Volumens und des Oberflächeninhalts darauf achten, dass die Höhe außerhalb des Prismas liegt.
Mit diesem Wissen bist du nun bestens vorbereitet, um das Volumen und den Oberflächeninhalt von Prismen zu berechnen.
Gerade und schiefe Prismen: Unterschiede und Anwendungen
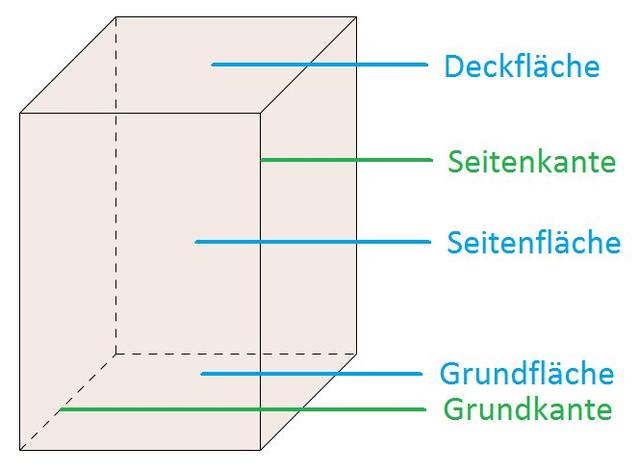
Ein gerades Prisma ist ein Prisma, bei dem die Kanten senkrecht auf der Grundfläche stehen. Die Höhe des Prismas liegt innerhalb des Prismas, und die Mantelfläche wird durch gleichlange, parallele Kanten verbunden. Gerade Prismen sind in der Geometrie am häufigsten anzutreffen und haben viele praktische Anwendungen.
Ein schiefes Prisma hingegen hat Kanten, die nicht senkrecht auf der Grundfläche stehen, sondern schräg. Bei schiefen Prismen liegt die Höhe außerhalb des Prismas. Die Mantelfläche wird immer noch durch parallele Kanten gebildet, aber sie sind nicht mehr gleich lang. Schiefe Prismen sind weniger gebräuchlich als gerade Prismen, finden aber dennoch in einigen Bereichen Anwendung.
Gerade Prismen werden oft in der Architektur verwendet, zum Beispiel als Dachform für Gebäude oder als Säulenkonstruktionen. Sie bieten eine stabile Struktur und können verschiedene Formen haben, je nach den Anforderungen des Designs.
Schiefe Prismen werden seltener verwendet, finden aber dennoch Verwendung in bestimmten Konstruktions- oder Designprojekten. Sie können interessante visuelle Effekte erzeugen und werden manchmal in Kunstwerken oder Skulpturen eingesetzt.
Insgesamt bieten sowohl gerade als auch schiefe Prismen vielfältige Möglichkeiten für kreative Gestaltung und praktische Anwendungen in verschiedenen Bereichen wie Architektur, Design und Kunst.
Zusammenfassend sind Prismen geometrische Formen, die aus einer Basis, Seitenflächen und Spitzen bestehen. Sie werden in verschiedenen Bereichen wie Optik und Mathematik verwendet und haben verschiedene Arten, je nach der Anzahl der Seitenflächen. Prismen spielen eine wichtige Rolle bei der Lichtbrechung und -reflexion sowie bei der Berechnung von Volumen und Oberfläche.