Was sind Primfaktoren? Eine einfache Erklärung und Beispiele

Primfaktoren sind die grundlegenden Faktoren, aus denen eine Zahl zusammengesetzt ist. Sie sind die kleinsten Zahlen, die diese Zahl ohne Rest teilen können. Das Verständnis der Primfaktoren hilft uns, komplexe Zahlen in ihre einfachsten Bestandteile zu zerlegen und sie besser zu analysieren. In diesem Artikel werden wir uns näher mit dem Konzept der Primfaktoren befassen und lernen, wie wir sie berechnen können.

Primfaktoren: Was sie sind und wie man sie berechnet

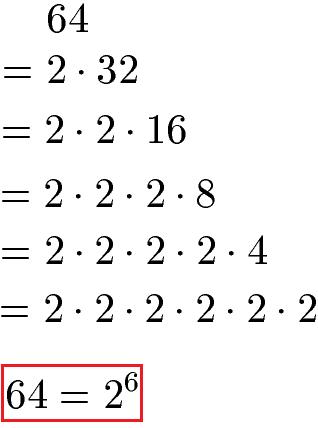
Was sind Primfaktoren?

Primfaktoren sind die Faktoren einer Zahl, die Primzahlen sind. Eine Primzahl ist eine natürliche Zahl größer als 1, die nur durch 1 und sich selbst ohne Rest teilbar ist. Bei der Primfaktorzerlegung wird eine Zahl als das Produkt ihrer Primfaktoren dargestellt.

Wie berechnet man Primfaktoren?

Um die Primfaktoren einer Zahl zu berechnen, testet man einfach, durch welche Primzahlen sich die Zahl ohne Rest teilen lässt. Man beginnt mit der kleinsten Primzahl (meistens 2) und teilt die Zahl so lange durch diese Primzahl, bis sie nicht mehr ohne Rest teilbar ist. Dann geht man zur nächsten größeren Primzahl über und wiederholt den Vorgang. Dies wird solange fortgesetzt, bis das Divisionsergebnis eine Primzahl ist.

Beispiel:
Angenommen, wir möchten die Primfaktoren von 48 berechnen.
Zuerst testen wir 48 auf Teilbarkeit durch 2. Da 48 durch 2 ohne Rest teilbar ist, ergibt sich das Divisionsergebnis 24. Wir setzen also unsere Berechnung fort und teilen nun 24 erneut durch 2: 24/2 = 12. Auch hier ist das Ergebnis ohne Rest teilbar, also setzen wir fort: 12/2 = 6. Nun teilen wir weiter: 6/2 = 3. Da die Zahl jetzt eine Primzahl ist (und keine weiteren Faktoren hat), können wir unseren Berechnungsvorgang abschließen. Die Primfaktorzerlegung von 48 lautet also: 2 * 2 * 2 * 2 * 3.

Ein weiteres Beispiel ist die Primfaktorzerlegung von 18.
Hier testen wir zuerst auf Teilbarkeit durch 2: 18/2 = 9. Da das Ergebnis nicht ohne Rest teilbar ist, gehen wir zur nächsten Primzahl über, in diesem Fall die Zahl 3. Wir teilen also weiter: 9/3 = 3. Auch hier handelt es sich um eine Primzahl, daher endet unsere Berechnung. Die Primfaktorzerlegung von 18 lautet somit: 2 * 3 * 3.

Die Primfaktorzerlegung ermöglicht es uns, komplexe Zahlen in ihre grundlegenden Bestandteile zu zerlegen und bietet eine wichtige Grundlage für weitere mathematische Berechnungen und Analysen.

Die Bedeutung von Primfaktoren und ihre Berechnung

Die Primfaktorzerlegung ist eine wichtige mathematische Methode, um eine Zahl in ihre Grundbausteine, die Primzahlen, zu zerlegen. Diese Zerlegung ermöglicht es uns, komplexe Zahlen zu analysieren und zu verstehen.

Warum sind Primfaktoren wichtig?

Primzahlen sind Zahlen, die nur durch 1 und sich selbst ohne Rest teilbar sind. Sie spielen eine entscheidende Rolle in der Mathematik, da sie die Grundbausteine für alle anderen Zahlen darstellen. Durch die Identifizierung der Primfaktoren einer Zahl können wir ihr eindeutiges Muster erkennen und sie besser analysieren.

Wie berechnet man Primfaktoren?

Um die Primfaktoren einer Zahl zu berechnen, teilen wir sie so lange wie möglich durch die kleinste mögliche Primzahl. Wenn wir eine Teilung ohne Rest erhalten, haben wir einen Primfaktor gefunden. Wir wiederholen diesen Schritt mit dem Divisionsergebnis, bis wir nur noch Primzahlen übrig haben.

Zum Beispiel nehmen wir die Zahl 48:

1. Wir testen 48 auf Teilbarkeit durch 2: 48 / 2 = 24
2. Dann testen wir 24 auf Teilbarkeit durch 2: 24 / 2 = 12
3. Weiter testen wir 12 auf Teilbarkeit durch 2: 12 / 2 =6
4. Danach testen wir 6 auf Teilbarkeit durch 2: 6 / 2 =3

Da 3 eine Primzahl ist, können wir aufhören. Die Primfaktorzerlegung von 48 lautet also: 2 * 2 * 2 * 2 * 3.

Ein weiteres Beispiel ist die Zahl 18:

1. Wir testen 18 auf Teilbarkeit durch 2: nicht teilbar
2. Dann testen wir es auf Teilbarkeit durch die nächste Primzahl, nämlich 3:18 /3 =6

Da wir nun eine Primzahl haben, können wir mit der Berechnung abschließen. Die Primfaktorzerlegung von 18 lautet also: 2 *3 *3.

Primfaktoren erklärt: Wie man eine Zahl in Primzahlen zerlegt

Was ist eine Primfaktorzerlegung?

Eine Primfaktorzerlegung ist eine Methode, um eine natürliche Zahl als Produkt von Primzahlen darzustellen. Dabei werden die einzelnen Faktoren, aus denen das Produkt besteht, als Primfaktoren bezeichnet. Die Primfaktordarstellung einer Zahl ist bis auf die Reihenfolge der Primfaktoren eindeutig.

Wie macht man eine Primfaktorzerlegung?

Die Durchführung einer Primfaktorzerlegung ist recht einfach. Man testet nacheinander, durch welche Primzahlen sich die Zahl ohne Rest teilen lässt. Beginnend mit der kleinsten Primzahl (2) wird geprüft, ob die Zahl durch diese teilbar ist. Falls ja, wird das Divisionsergebnis erneut auf Teilbarkeit getestet und dieser Vorgang wiederholt, bis nur noch eine Primzahl übrig bleibt.

Beispiel:
Wir möchten die Zahl 48 in ihre Primfaktoren zerlegen.
1. Schritt: 48 ist durch 2 teilbar. Somit gilt: 48 = 2 * 24.
2. Schritt: Auch 24 ist durch 2 teilbar. Es ergibt sich: 24 = 2 * 12.
3. Schritt: Weiterhin kann man feststellen, dass auch 12 durch 2 teilbar ist. Somit gilt nun: 12 = 2 * 6.
4. Schritt: Nun lässt sich erkennen, dass auch die Zahl 6 durch die kleinste verbleibende Primzahl (2) teilbar ist. Es ergibt sich: 6 = 2 * 3.
5. Schritt: Da die Zahl 3 eine Primzahl ist, kann man den Vorgang hier beenden.
Die Primfaktorzerlegung von 48 lautet also: 48 = 2 * 2 * 2 * 2 * 3.

Ein weiteres Beispiel:
Wir möchten die Zahl 18 in ihre Primfaktoren zerlegen.
1. Schritt: Die Zahl ist nicht durch die kleinste Primzahl (2) teilbar.
2. Schritt: Nun testen wir, ob die Zahl durch die nächste Primzahl (3) teilbar ist. Tatsächlich gilt: 18 = 3 * 6.
3. Schritt: Auch die verbleibende Zahl (6) lässt sich nochmals durch die Primzahl (3) teilen. Somit ergibt sich: 6 = 3 * 2.
Die Primfaktorzerlegung von 18 lautet also: 18 = 2 * 3 * 3.

Die Primfaktorzerlegung ermöglicht es uns, komplexe Zahlen auf ihre grundlegenden Bestandteile zurückzuführen und erleichtert dadurch das Verständnis und weitere Berechnungen mit diesen Zahlen.

Alles über Primfaktoren: Definition und Berechnungsmethoden

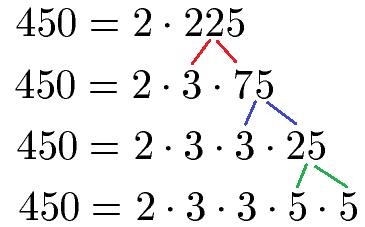
Definition von Primfaktoren

Bei der Primfaktorzerlegung wird eine natürliche Zahl als das Produkt ihrer Primfaktoren dargestellt. Ein Primfaktor ist dabei ein Faktor, der eine Primzahl ist. Eine Primzahl ist eine natürliche Zahl größer als 1, die nur durch 1 und sich selbst ohne Rest teilbar ist.

Die Primfaktordarstellung einer Zahl ist bis auf die Reihenfolge der Primfaktoren eindeutig. Das bedeutet, dass jede natürliche Zahl eindeutig als Produkt ihrer Primfaktoren dargestellt werden kann.

Berechnungsmethoden für die Primfaktorzerlegung

Es gibt verschiedene Methoden, um die Primfaktorzerlegung einer Zahl zu berechnen. Eine einfache Methode besteht darin, die Zahl nacheinander durch alle möglichen Primzahlen zu teilen und dabei zu prüfen, ob sie ohne Rest teilbar ist.

1. Teste die Teilbarkeit durch 2: Wenn die Zahl gerade ist, dann teile sie durch 2 und notiere den Faktor 2.
2. Teste die Teilbarkeit durch 3: Addiere alle Ziffern der Zahl und prüfe, ob diese Summe durch 3 ohne Rest teilbar ist. Wenn ja, teile die Zahl durch 3 und notiere den Faktor 3.
3. Teste die Teilbarkeit durch weitere Primzahlen: Teile die Zahl nacheinander durch alle weiteren bekannten Primzahlen und notiere jeden gefundenen Faktor.

Wiederhole diese Schritte, bis das Divisionsergebnis eine Primzahl ist. Die Primfaktorzerlegung der Zahl besteht dann aus allen notierten Faktoren.

Beispiel:
Wir möchten die Primfaktorzerlegung der Zahl 48 berechnen.
1. 48 ist durch 2 ohne Rest teilbar, also notieren wir den Faktor 2 und teilen die Zahl durch 2: 48 = 2 * 24.
2. Auch 24 ist durch 2 ohne Rest teilbar, also notieren wir erneut den Faktor 2 und teilen die Zahl erneut durch 2: 24 = 2 * 12.
3. Weiterhin ist auch 12 durch 2 ohne Rest teilbar: 12 = 2 *6.
4. Nun ist aber die Zahl nicht mehr durch 2 ohne Rest teilbar. Wir testen nun die Teilbarkeit durch die nächste Primzahl, also durch die Zahl 3. Da sich auch hierbei keine Teilbarkeit ergibt, können wir aufhören zu testen.
Die Primfaktorzerlegung von 48 lautet daher: 48 = 2 *2 *2 *3.

Für komplexere Zahlen kann es erforderlich sein, weitere Primzahlen zu testen und den Prozess fortzusetzen, bis das Divisionsergebnis eine Primzahl ist. Mit diesen Berechnungsmethoden lässt sich jedoch jede natürliche Zahl eindeutig als Produkt ihrer Primfaktoren darstellen.

Schritt-für-Schritt-Anleitung zur Bestimmung von Primfaktoren

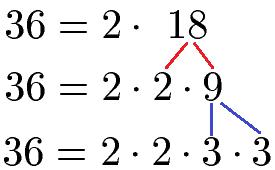
Schritt 1: Wähle eine natürliche Zahl

Wähle eine beliebige natürliche Zahl aus, die du in Primfaktoren zerlegen möchtest.

Schritt 2: Beginne mit der kleinsten Primzahl

Starte mit der kleinsten Primzahl, das ist die Zahl 2. Überprüfe, ob die gewählte Zahl ohne Rest durch 2 teilbar ist.

– Falls ja: Teile die Zahl durch 2 und notiere den Faktor 2.
– Falls nein: Gehe zum nächsten Schritt.

Schritt 3: Teste die nächste Primzahl

Gehe zur nächsten Primzahl nach der Reihe (also 3, 5, 7, usw.) und überprüfe erneut, ob die verbleibende Zahl ohne Rest durch diese Primzahl teilbar ist.

– Falls ja: Teile die Zahl durch diese Primzahl und notiere den Faktor.
– Falls nein: Gehe zur nächsten Primzahl weiter.

Schritt 4: Wiederhole Schritt 3

Fahre fort mit Schritt 3, bis du alle möglichen Primzahlen getestet hast oder das Divisionsergebnis selbst eine Primzahl ist.

Schritt 5: Notiere die Ergebnisse

Notiere alle gefundenen Primfaktoren in der Reihenfolge, in der du sie gefunden hast. Die Reihenfolge spielt für das Ergebnis keine Rolle.

Das war’s! Du hast erfolgreich eine Primfaktorzerlegung durchgeführt.

Primfaktorzerlegung einfach erklärt: So funktioniert es

Was ist eine Primfaktorzerlegung?

Bei der Primfaktorzerlegung wird eine Zahl als das Produkt ihrer Primfaktoren dargestellt. Das bedeutet, dass man die Zahl nur als Produkt von Primzahlen schreibt. Jede natürliche Zahl kann eindeutig als solches Produkt ausgedrückt werden. Die einzelnen Faktoren, aus denen das Produkt besteht, nennt man Primfaktoren.

Wie mache ich eine Primfaktorzerlegung?

Die Primfaktorzerlegung einer Zahl erfolgt durch einfaches Testen, durch welche Primzahlen sich die Zahl ohne Rest teilen lässt. Man beginnt mit der kleinsten Primzahl und testet nacheinander alle größeren Primzahlen. Wenn die Zahl durch eine bestimmte Primzahl teilbar ist, teilt man sie durch diese und notiert den Faktor. Anschließend wiederholt man den Vorgang mit dem Ergebnis der Division, bis man nur noch eine Primzahl erhält.

Beispiel:
Um die Primfaktorzerlegung von 48 zu berechnen, testet man zuerst die Teilbarkeit durch 2. Da 48 ohne Rest durch 2 teilbar ist, ergibt sich der Faktor 2. Man dividiert nun das Ergebnis (24) erneut durch 2 und erhält wieder den Faktor 2. Diesen Schritt wiederholt man so lange, bis keine weitere Teilbarkeit mehr möglich ist. In diesem Fall ergibt sich die Zerlegung 48 = 2 * 2 * 2 * 2 * 3.

Ein weiteres Beispiel ist die Primfaktorzerlegung von 18. Hier testet man zuerst die Teilbarkeit durch 2, jedoch ist 18 nicht durch 2 teilbar. Man geht also zur nächsten Primzahl über, in diesem Fall die Zahl 3. Da 18 ohne Rest durch 3 teilbar ist, ergibt sich der Faktor 3. Die Zerlegung lautet somit 18 = 2 * 3 * 3.

Die Primfaktorzerlegung ermöglicht es uns, komplexe Zahlen auf ihre grundlegenden Bestandteile zurückzuführen und erleichtert damit weitere Rechenoperationen oder das Finden von Teilmengen bestimmter Zahlen.

Die Primfaktoren sind die kleinsten und unteilbaren Teiler einer Zahl. Sie spielen eine wichtige Rolle in der Mathematik und ermöglichen es uns, große Zahlen auf ihre grundlegenden Bestandteile zu reduzieren. Das Wissen über Primfaktoren hilft uns bei der Lösung von mathematischen Problemen und ist auch in anderen Bereichen wie Kryptographie von großer Bedeutung.