Nullstellen sind die Wurzeln oder Lösungen einer Gleichung, bei denen der Funktionswert null ist. Sie spielen eine wichtige Rolle in der Mathematik und werden verwendet, um den Verlauf von Funktionen zu analysieren und Probleme zu lösen. In diesem Artikel werden wir uns genauer mit dem Konzept der Nullstellen und ihrer Bedeutung beschäftigen.
Definition und Bedeutung von Nullstellen in Funktionen
Eine Nullstelle einer Funktion ist ein x-Wert, für den der Funktionswert gleich null ist. Es handelt sich um einen Schnitt- oder Berührpunkt des Funktionsgraphen mit der x-Achse. Um die Nullstellen einer Funktion zu finden, löst man die Gleichung f(x) = 0. Es kann vorkommen, dass eine bestimmte Stelle mehrfach als Lösung ermittelt wird, insbesondere bei rationalen oder Potenzfunktionen.
Beispiel: Die Funktion f(x) = x+1 hat die einfache Nullstelle x = -1. Der Graph schneidet die x-Achse also bei (-1|0).
In der Differenzialrechnung betrachtet man auch die Nullstellen der Ableitungen einer Funktion. Nullstellen der ersten Ableitung können Extremstellen sein, während Nullstellen der zweiten Ableitung Wendepunkte anzeigen.
Die Funktion f(x) = (2-x)e^x hat eine Nullstelle bei x = 2. Der Graph schneidet die x-Achse also bei (2|0).
Die Bedeutung von Nullstellen liegt darin, dass sie uns Informationen über das Verhalten des Funktionsgraphen geben. Sie zeigen uns Punkte, an denen die Funktion den Wert null annimmt und somit wichtige Schnitt- oder Berührungspunkte mit der x-Achse sind.
Es gibt verschiedene Methoden zur Bestimmung von Nullstellen, wie zum Beispiel das Lösen von Gleichungen algebraisch oder numerische Verfahren wie das Newton-Verfahren.
Nullstellen spielen auch eine Rolle in anderen mathematischen Gebieten wie der Physik oder Wirtschaftswissenschaften, wo sie zum Beispiel das Auftreten von Gleichgewichtspunkten oder das Erreichen bestimmter Werte anzeigen können.
Wie man Nullstellen einer Funktion findet und interpretiert
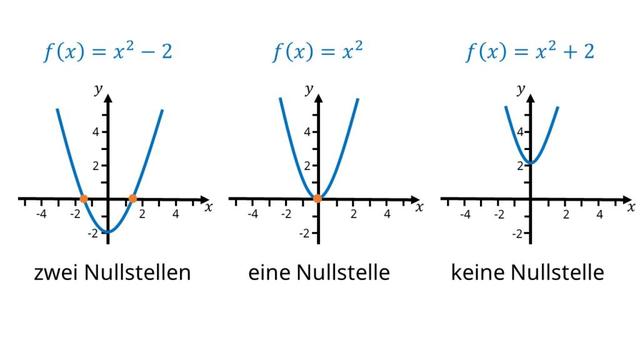
Die Nullstellen einer Funktion sind die x-Werte, für die der Funktionswert gleich null ist. Sie können gefunden werden, indem man die Gleichung f(x) = 0 löst. Bei rationalen oder Potenzfunktionen kann es vorkommen, dass eine bestimmte Stelle mehrfach als Lösung ermittelt wird. In solchen Fällen hat der Funktionsgraph an dieser Stelle einen Berührpunkt mit der x-Achse.
Ein Beispiel dafür ist die Funktion f(x) = x+1. Die Nullstelle dieser Funktion kann durch Lösen der Gleichung x+1=0 gefunden werden, was zu x=-1 führt. Der Graph von f schneidet also die x-Achse bei (-1|0).
In der Differenzialrechnung betrachtet man auch die Nullstellen der Ableitungen einer Funktion. Die Nullstellen der ersten Ableitung können Extremstellen sein, während die Nullstellen der zweiten Ableitung Wendepunkte sind.
Ein weiteres Beispiel ist die Funktion f(x) = (2-x)e^x. Die Graphen von f und ihrer Ableitungsfunktion f‘ sind in der Abbildung dargestellt.
In einem anderen Beispiel wird das Ölfeld seit Beginn des Jahres 1990 mit Bohrungen in mehreren Erdöl führenden Schichten erschlossen. Die momentane Förderrate aus diesem Ölfeld im Zeitraum von Anfang 1990 bis Ende 2009 kann durch eine Funktion modelliert werden. Der Graph dieser Funktion zeigt den Verlauf der Förderrate über die Zeit.
Ein ähnliches Modell wird verwendet, um den Zufluss von Wasser in ein Staubecken oberhalb eines Bergdorfes zu beschreiben. Hierbei kann die momentane Zuflussrate durch eine Funktion modelliert werden, deren Graph den Verlauf des Zuflusses über die Zeit zeigt.
In manchen Fällen fließen zwei Bäche in das Staubecken. In solchen Situationen können die momentanen Zuflussraten aus den beiden Bächen durch separate Funktionen beschrieben werden. Die Gesamtzuflussrate aus beiden Bächen kann dann durch eine weitere Funktion modelliert werden.
Es ist wichtig zu beachten, dass die Lösungsvorschläge nicht in der Verantwortung des Kultusministeriums liegen und dass diese Informationen nur als Beispiel dienen.
Anwendung der Nullstellen in der Differentialrechnung
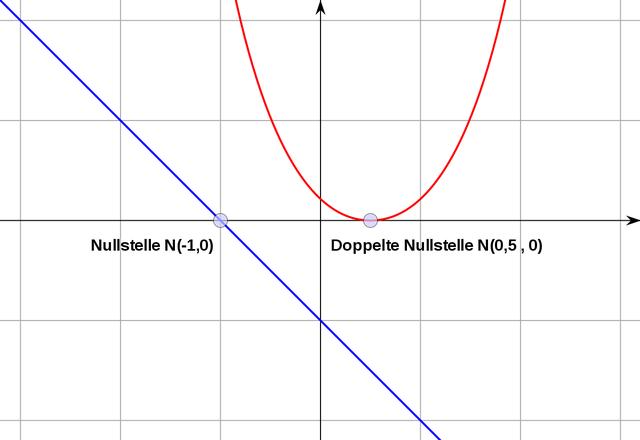
Die Nullstellen einer Funktion spielen eine wichtige Rolle in der Differentialrechnung. Sie können uns Informationen über das Verhalten des Funktionsgraphen geben.
Wenn wir die Nullstellen der Ableitung einer Funktion finden, können wir herausfinden, wo sich Extremstellen befinden. Eine Nullstelle der ersten Ableitung kann entweder ein Minimum oder ein Maximum sein. Eine Nullstelle der zweiten Ableitung wird als Wendepunkt bezeichnet.
Ein Beispiel für die Anwendung von Nullstellen in der Differentialrechnung ist die Funktion \(f(x) =(2-x)\cdot e^x\). Der Graph dieser Funktion und ihrer Ableitungsfunktion sind in der Abbildung dargestellt. Die Nullstellen der Ableitungsfunktion können uns Informationen über mögliche Extremstellen und Wendepunkte geben.
In einem anderen Beispiel betrachten wir ein Ölfeld, das seit 1990 mit Bohrungen erschlossen wird. Die momentane Förderrate aus diesem Ölfeld kann durch die Funktion \(f(t)=(1020-40t) \cdot e^{0,1 \cdot t}\) modelliert werden. Hierbei steht \(t\) für die Anzahl der Jahre seit 1990 und \(f(t)\) für die Förderrate in Tonnen pro Jahr. Durch das Finden von Nullstellen der Ableitungen dieser Funktion können wir mögliche Extremstellen im Zeitraum von 1990 bis 2009 identifizieren.
Ein weiteres Beispiel betrifft den Zufluss eines Baches in ein Staubecken während eines starken Regenfalls. Die momentane Zuflussrate aus dem Bach kann durch die Funktion \(f(t) = \frac14 t^3 -12t^2 +144t +250\) modelliert werden. Hierbei steht \(t\) für die Anzahl der Stunden seit Beginn des Regenfalls und \(f(t)\) für die Zuflussrate in Kubikmetern pro Stunde. Durch das Finden von Nullstellen der Ableitungen dieser Funktion können wir mögliche Extremstellen im Beobachtungszeitraum identifizieren.
In einem letzten Beispiel betrachten wir den Zufluss aus zwei Bächen in ein Staubecken. Die momentanen Zuflussraten aus den beiden Bächen können durch Funktionen \(f_a(t)\) und \(g_a(t)\) modelliert werden. Die Gesamtzuflussrate aus beiden Bächen kann durch eine Funktion \(h_a(t)\) modelliert werden. Durch das Finden von Nullstellen der Ableitungen dieser Funktionen können wir mögliche Extremstellen im Beobachtungszeitraum identifizieren.
Die Nullstellen einer Funktion sind also wichtige Punkte, um Informationen über das Verhalten des Funktionsgraphen zu erhalten und Extremstellen oder Wendepunkte zu finden.
Beispiel: Finden und interpretieren Sie die Nullstelle einer gegebenen Funktion
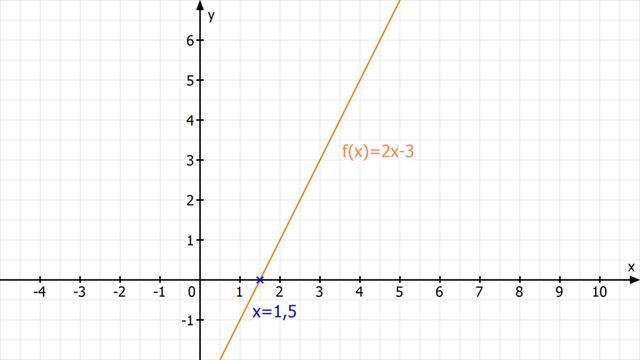
Eine Nullstelle einer Funktion ist ein x-Wert, bei dem der Funktionswert gleich null ist. Es handelt sich also um einen Schnitt- oder Berührpunkt des Funktionsgraphen mit der x-Achse. Um die Nullstellen einer Funktion zu finden, löst man die Gleichung f(x) = 0. Bei bestimmten Funktionen können mehrere Lösungen auftreten, zum Beispiel bei rationalen oder Potenzfunktionen. In diesem Fall kann eine bestimmte Stelle als Lösung mehrfach ermittelt werden.
Ein Beispiel für eine einfache Nullstelle ist die Funktion f(x) = x + 1. Um die Nullstelle zu finden, setzt man f(x) gleich null und löst die Gleichung auf: x + 1 = 0. Die Lösung ist x = -1. Der Graph von f schneidet also die x-Achse im Punkt (-1|0).
In der Differentialrechnung betrachtet man auch die Nullstellen der Ableitungen einer Funktion. Die Nullstellen der ersten Ableitung können Extremstellen sein, während die Nullstellen der zweiten Ableitung Wendepunkte darstellen.
Der gegebene Funktionsterm f(x) = (2-x)e^x beschreibt den Graphen einer Funktion. Die Abbildung zeigt sowohl den Graphen von f als auch den Graphen ihrer Ableitungsfunktion f‘. Die Lösungen zu den Aufgaben liegen nicht in der Verantwortung des Kultusministeriums.
Ein Ölfeld wird seit Anfang 1990 mit Bohrungen in verschiedenen Erdölschichten erschlossen. Die momentane Förderrate aus diesem Ölfeld kann durch die Funktion f(t) = (1020-40t)e^(0,1t) modelliert werden, wobei t die Anzahl der Jahre seit Beginn des Jahres 1990 ist. Der Graph von f zeigt die Förderrate im Zeitraum von 1990 bis 2009.
In einem Staubecken oberhalb eines Bergdorfes fließt ein Bach. Die momentane Zuflussrate aus diesem Bach kann durch die Funktion f(t) = (1/4)t^3 -12t^2 +144t +250 modelliert werden, wobei t die Anzahl der Stunden seit Beginn des Beobachtungszeitraums ist. Der Beobachtungszeitraum dauert von t = 0 bis t = 24.
Wenn zwei Bäche in das Staubecken fließen, können ihre momentanen Zuflussraten durch die Funktionen f_a(t) und g_a(t) beschrieben werden. Die Gesamtzuflussrate aus beiden Bächen wird durch die Funktion h_a(t) modelliert. Die genauen Funktionsgleichungen sind gegeben und hängen von einem Parameter a ab.
Die Lösungsvorschläge zu den Aufgaben liegen nicht in der Verantwortung des Kultusministeriums.
Modellierung von Zufluss- und Förderraten mit Hilfe von Funktionen und deren Nullstellen
Die Modellierung von Zufluss- und Förderraten mit Hilfe von Funktionen und deren Nullstellen ist ein wichtiger Aspekt in der Mathematik. Dabei werden mathematische Funktionen verwendet, um den Verlauf von Zufluss- oder Förderraten über einen bestimmten Zeitraum zu beschreiben.
Ein Beispiel für die Modellierung einer Förderrate ist das Ölfeld, das seit Beginn des Jahres 1990 mit Bohrungen erschlossen wird. Die momentane Förderrate aus diesem Ölfeld kann durch die Funktion \(f(t)=(1020-40t) \cdot e^{0,1 \cdot t}\) modelliert werden. Hierbei wird \(t\) als Maßzahl zur Einheit 1 Jahr und \(f(t)\) als Maßzahl zur Einheit 1000 Tonnen pro Jahr aufgefasst. Der Zeitpunkt \(t=0\) entspricht dem Beginn des Jahres 1990.
Um die Nullstellen dieser Funktion zu finden, setzt man \(f(t)\) gleich null und löst die Gleichung nach \(t\) auf. In diesem Fall erhält man eine Gleichung der Form \((1020-40t) \cdot e^{0,1 \cdot t} = 0\). Durch Lösen dieser Gleichung kann man die Zeitpunkte ermitteln, zu denen keine Förderung stattfindet.
Ein ähnliches Prinzip gilt auch für die Modellierung von Zuflussraten. Zum Beispiel fließt in ein Staubecken oberhalb eines Bergdorfes ein Bach. Die momentane Zuflussrate aus diesem Bach kann an einem Tag mit starken Regenfällen durch die Funktion \(f(t) = \frac14 t^3 -12t^2 +144t +250\) modelliert werden. Hierbei wird \(t\) als Maßzahl zur Einheit 1 Stunde und \(f(t)\) als Maßzahl zur Einheit \(\frac{m^3}{h}\) aufgefasst. Der Beobachtungszeitraum beginnt zum Zeitpunkt \(t = 0\) und endet zum Zeitpunkt \(t = 24\).
Um die Nullstellen dieser Funktion zu finden, setzt man \(f(t)\) gleich null und löst die Gleichung nach \(t\) auf. In diesem Fall erhält man eine Gleichung der Form \(\frac14 t^3 -12t^2 +144t +250 = 0\). Durch Lösen dieser Gleichung kann man die Zeitpunkte ermitteln, zu denen kein Zufluss aus dem Bach stattfindet.
Die Nullstellen einer Funktion sind also von großer Bedeutung bei der Modellierung von Zufluss- und Förderraten. Sie geben die Zeitpunkte an, zu denen keine Zuflüsse oder Förderungen stattfinden. Durch das Lösen der entsprechenden Gleichungen können diese Nullstellen ermittelt werden.
Zusammenhang zwischen Nullstellen und dem Verhalten von Funktionen im Unendlichen
Der Zusammenhang zwischen Nullstellen und dem Verhalten von Funktionen im Unendlichen ist eng miteinander verknüpft. Wenn eine Funktion eine Nullstelle hat, bedeutet dies, dass der Funktionsgraph die x-Achse schneidet oder berührt. Dies kann anhand des Funktionswertes f(x0) = 0 festgestellt werden.
Wenn eine Funktion eine doppelte, vierfache, sechsfache usw. Nullstelle hat, bedeutet dies, dass der Funktionsgraph einen Berührpunkt mit der x-Achse hat. Bei einer einfachen, dreifachen, fünffachen usw. Nullstelle schneidet der Funktionsgraph die x-Achse.
Ein Beispiel hierfür ist die Normalparabel y = x^2. Der Ursprung (0|0) ist eine doppelte Nullstelle, da der Funktionswert f(0) = 0 ist. Der Graph schneidet die x-Achse jedoch nicht an dieser Stelle.
In der Differenzialrechnung betrachtet man auch die Nullstellen der Ableitungen einer Funktion. Die Nullstellen der ersten Ableitung können Extremstellen sein und die Nullstellen der zweiten Ableitung können Wendestellen sein.
Zum Beispiel betrachten wir die Funktion f(x) = (2-x)e^x. Ihr Graph und der Graph ihrer Ableitungsfunktion sind in Abbildung dargestellt.
Es liegt in Ihrer Verantwortung zu überprüfen, ob Ihre Lösungsvorschläge korrekt sind.
Zusammenfassend sind Nullstellen in der Mathematik die Werte, die einer Funktion entsprechen, wenn sie den Wert Null annimmt. Sie sind von großer Bedeutung für die Analyse und Lösung mathematischer Probleme, da sie Informationen über Schnittpunkte und Gleichgewichtspunkte liefern können. Durch das Finden von Nullstellen können wir auch Graphen zeichnen und Funktionen lösen.

