Alles über Diagonalen: Entdecke die verschiedenen Arten!

Diagonalen sind eine wichtige geometrische Eigenschaft von Figuren. Sie verbinden nicht benachbarte Ecken und schaffen dadurch neue Beziehungen im Raum. In diesem Artikel werden wir uns eingehend mit dem Konzept der Diagonalen befassen und ihre Bedeutung in verschiedenen mathematischen und geometrischen Zusammenhängen untersuchen. Wir werden erkunden, wie Diagonalen in Quadraten, Rechtecken, Dreiecken und anderen Figuren auftreten können und welche interessanten Eigenschaften sie besitzen. Lassen Sie uns gemeinsam die faszinierende Welt der Diagonalen entdecken!

Die Bedeutung von Diagonalen in Vielecken und Körpern

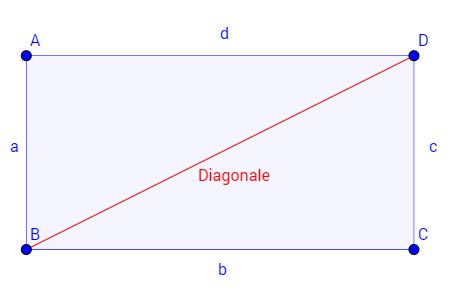
Vielecke:

Eine Diagonale ist eine Strecke, die zwei nicht benachbarte Eckpunkte in einem Vieleck miteinander verbindet. Sie schneidet dabei keine Seiten des Vielecks. Eine Diagonale kann sowohl innerhalb des Vielecks liegen als auch außerhalb davon verlaufen. Diagonalen spielen eine wichtige Rolle in der Geometrie von Vielecken, da sie zusätzliche Informationen über die Struktur und Symmetrie des Vielecks liefern können.

In einem Dreieck gibt es beispielsweise drei Diagonalen, die jeweils von einem Eckpunkt zu dem gegenüberliegenden Eckpunkt führen. Diese Diagonalen teilen das Dreieck in drei kleinere Dreiecke auf und haben verschiedene Eigenschaften wie Länge und Winkel.

Körper:

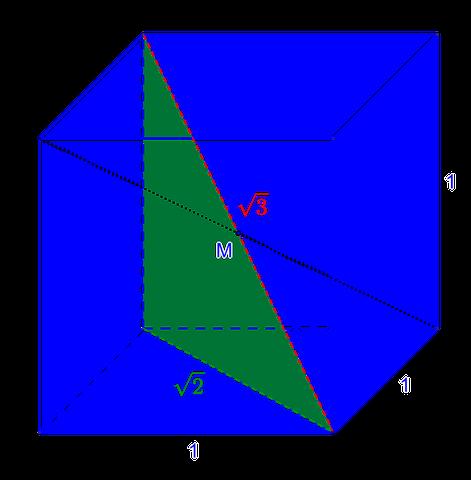
Auch in Körpern wie Quadern oder Würfeln spielen Diagonalen eine bedeutende Rolle. Im Quader gibt es beispielsweise verschiedene Arten von Diagonalen: die Flächendiagonale und die Raumdiagonale.

Die Flächendiagonale erstreckt sich diagonal über eine Rechtecksfläche des Quaders. Sie taucht auf jeder Seite des Quaders zweimal auf und hat immer die gleiche Länge. Die Flächendiagonalen teilen den Quader in vier gleich große Dreiecke auf.

Die Raumdiagonale hingegen bildet die größte Strecke, die in einem Würfel oder Quader gezogen werden kann. Sie erstreckt sich vom einen Eckpunkt zum räumlich gegenüberliegenden Eckpunkt und verläuft durch den Mittelpunkt des Körpers. Die Raumdiagonale teilt den Quader in zwei Pyramiden auf und hat eine größere Länge als die Flächendiagonalen.

Insgesamt tragen Diagonalen dazu bei, die Struktur und Symmetrie von Vielecken und Körpern besser zu verstehen und können bei der Berechnung von Eigenschaften wie Länge, Winkel und Volumen helfen.

Arten von Diagonalen: Flächendiagonalen und Raumdiagonalen

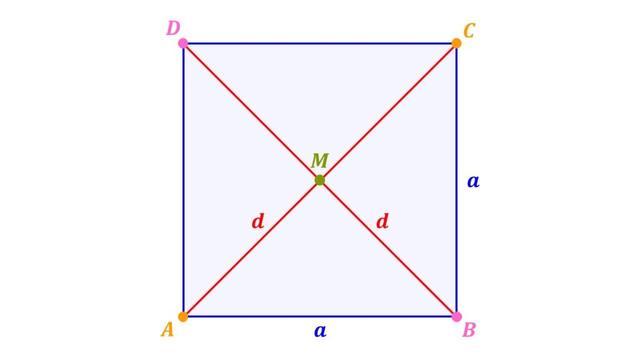
Flächendiagonalen

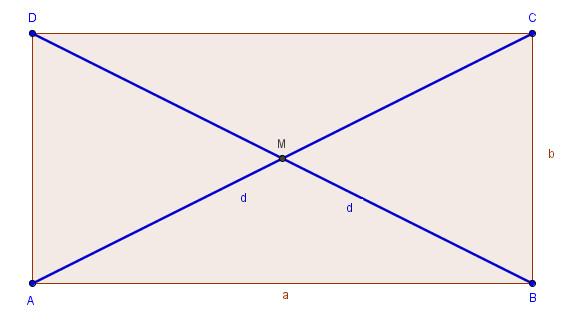
Flächendiagonalen sind Diagonalen, die sich innerhalb einer Fläche eines Vielecks oder eines Körpers erstrecken. Sie verbinden zwei nicht benachbarte Eckpunkte miteinander. Eine Flächendiagonale ist zum Beispiel eine Strecke, die in einem Rechteck von einer Ecke zur gegenüberliegenden Ecke verläuft. Im Quader gibt es mehrere Flächendiagonalen, die sich diagonal über eine Rechtecksfläche erstrecken.

– Flächendiagonalen verlaufen innerhalb einer Ebene.
– Sie können auf jeder Seite des Körpers zweimal auftreten.
– Die Anzahl der Flächendiagonalen in einem n-Eck kann mit einer Formel berechnet werden.

Raumdiagonalen

Raumdiagonalen sind Diagonalen, die sich im Raum erstrecken und den gesamten Körper durchqueren. Sie verbinden zwei nicht benachbarte Eckpunkte miteinander und bilden die längste Strecke, die in einem Würfel oder Quader gezogen werden kann.

– Raumdiagonalen verlaufen durch den gesamten Körper.
– Sie treffen sich genau in der Mitte zwischen den beiden Endpunkten.
– Die Anzahl der Raumdiagonalen in einem n-Eck kann ebenfalls mit einer Formel berechnet werden.

Zusammenfassend gibt es also zwei Arten von Diagonalen: Flächendiagonalen, die innerhalb eines Vielecks oder eines Körpers verlaufen, und Raumdiagonalen, die den gesamten Körper durchqueren. Beide Diagonalen verbinden zwei nicht benachbarte Eckpunkte miteinander und haben unterschiedliche Eigenschaften.

Beispiele für Diagonalen im Quader

Flächendiagonalen

Im Quader gibt es Flächendiagonalen, die sich diagonal über eine Rechtecksfläche erstrecken. Sie verbinden jeweils zwei gegenüberliegende Eckpunkte des Rechtecks. Da der Quader sechs Rechtecksflächen hat, gibt es insgesamt vier Flächendiagonalen. Diese Diagonalen haben alle die gleiche Länge und sind in der Farbe Türkis markiert.

Raumdiagonale

Die Raumdiagonale ist die größte Strecke, die in einem Quader gezogen werden kann. Sie verbindet den einen Eckpunkt des Quaders mit dem räumlich gegenüber liegenden Eckpunkt. Die Raumdiagonale erstreckt sich durch den gesamten Körper und teilt ihn in zwei gleich große Pyramiden auf. Der Mittelpunkt des Quaders liegt genau in der Mitte dieser Diagonale.

Es gibt mehrere Raumdiagonalen im Quader, da es verschiedene Möglichkeiten gibt, zwei gegenüberliegende Eckpunkte zu verbinden. Jede Raumdiagonale hat dieselbe Länge und ist in Rot markiert.

Durch die Flächendiagonalen und Raumdiagonalen entsteht ein Netzwerk von Verbindungen innerhalb des Quaders, das seine Struktur und Symmetrie ausmacht.

Wie man die Anzahl der Diagonalen in einem n-Eck berechnet

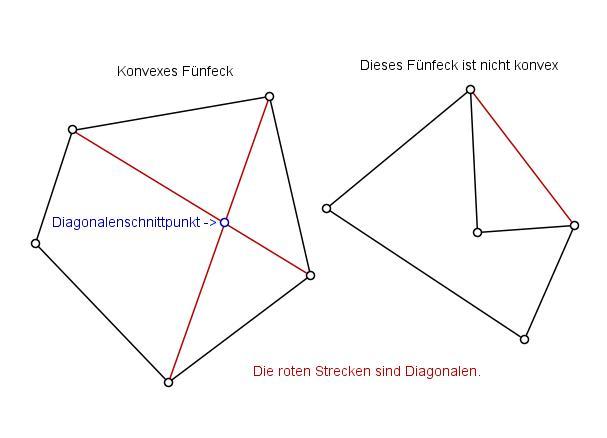
Einführung

In einem n-Eck, auch Polygon genannt, können Diagonalen gezogen werden. Eine Diagonale ist eine Strecke, die zwei nicht benachbarte Eckpunkte des Polygons verbindet. Die Anzahl der Diagonalen in einem n-Eck kann mit einer Formel berechnet werden.

Formel zur Berechnung der Anzahl der Diagonalen

Die Formel zur Berechnung der Anzahl der Diagonalen in einem n-Eck lautet: D = (n * (n – 3)) / 2. Dabei steht D für die Anzahl der Diagonalen und n für die Anzahl der Seiten des Polygons.

Beispiel:
Angenommen, wir haben ein Fünfeck (n = 5). Wir setzen den Wert von n in die Formel ein: D = (5 * (5 – 3)) / 2 = (5 * 2) / 2 = 10 / 2 = 5. In einem Fünfeck gibt es also insgesamt fünf Diagonalen.

Anwendung der Formel

Die Formel kann verwendet werden, um die Anzahl der Diagonalen in beliebigen n-Ecken zu berechnen. Es ist wichtig zu beachten, dass eine Seite des Polygons nicht als Diagonale betrachtet wird.

Zusammenfassend lässt sich sagen, dass die Anzahl der Diagonalen in einem n-Eck mit Hilfe der Formel D = (n * (n – 3)) / 2 berechnet werden kann.

Die Rolle von Diagonalen in der Geometrie

Bedeutung von Diagonalen in Vielecken und Körpern

Diagonalen spielen eine wichtige Rolle in der Geometrie, insbesondere in Vielecken und Körpern. Eine Diagonale ist eine Strecke, die zwei nicht benachbarte Eckpunkte miteinander verbindet. Sie ermöglicht es uns, verschiedene Eigenschaften und Beziehungen innerhalb des geometrischen Objekts zu untersuchen.

In einem Vieleck können Diagonalen dazu verwendet werden, um die Anzahl der möglichen Dreiecke zu bestimmen, die durch Verbinden der Eckpunkte entstehen. Je nach Art des Vielecks gibt es unterschiedliche Formeln zur Berechnung der Anzahl der Diagonalen.

Auch in Körpern wie dem Quader spielen Diagonalen eine wichtige Rolle. Hier gibt es zwei Arten von Diagonalen: die Flächendiagonale und die Raumdiagonale. Die Flächendiagonale erstreckt sich diagonal über eine Rechtecksfläche und taucht auf jeder Seite des Quaders zweimal auf. Sie kann dazu verwendet werden, um den Abstand zwischen den gegenüberliegenden Ecken zu berechnen.

Die Raumdiagonale hingegen bildet die längste Strecke, die in einem Würfel oder Quader gezogen werden kann. Sie erstreckt sich vom einen Ende des Körpers zum räumlich gegenüberliegenden Punkt. Die Raumdiagonale teilt den Körper genau in der Mitte und ermöglicht es uns, den Mittelpunkt zu bestimmen.

Anwendung der Formel zur Berechnung der Anzahl von Diagonalen

In einem n-Eck kann die Anzahl der Diagonalen mit folgender Formel berechnet werden: (n * (n-3)) / 2. Diese Formel ergibt sich aus der Tatsache, dass jede Ecke mit jeder anderen Ecke verbunden werden kann, jedoch die Diagonalen zwischen benachbarten Eckpunkten nicht gezählt werden.

Um die Anzahl der Diagonalen in einem n-Eck zu berechnen, multiplizieren wir die Anzahl der Eckpunkte (n) mit der Anzahl der möglichen Verbindungen zu den anderen Eckpunkten (n-3). Da jede Verbindung zweimal gezählt wird und wir nur eine Hälfte davon zählen möchten, teilen wir das Ergebnis durch 2.

Diese Formel ist sehr nützlich, um schnell die Anzahl der Diagonalen in verschiedenen Vielecken zu bestimmen und ermöglicht es uns, weitere Eigenschaften und Beziehungen innerhalb des geometrischen Objekts zu erforschen.

Praktische Anwendungen von Diagonalen in verschiedenen Formen und Figuren

Anwendungen von Diagonalen im Quader:

– Die Flächendiagonale im Quader kann verwendet werden, um die Länge einer Rechtecksfläche zu berechnen. Sie ist nützlich, wenn man beispielsweise die Größe eines Bildschirms oder die Diagonale eines Fernsehers bestimmen möchte.
– Die Raumdiagonale im Quader kann verwendet werden, um den Abstand zwischen zwei gegenüberliegenden Ecken zu messen. Dies kann zum Beispiel bei der Planung eines Raumes oder beim Bau von Möbelstücken hilfreich sein.

Anwendungen von Diagonalen im Würfel:

– Die Raumdiagonale im Würfel kann verwendet werden, um den Abstand zwischen zwei gegenüberliegenden Ecken zu messen. Dies ist besonders nützlich, wenn man den Platzbedarf für einen Gegenstand in einem Würfelraum berechnen möchte.
– Die Raumdiagonale kann auch dazu verwendet werden, die maximale Länge einer Strecke innerhalb des Würfels zu bestimmen. Dies ist wichtig, wenn man beispielsweise eine Kabelverbindung in einem Würfelraum verlegen muss.

Die Verwendung von Diagonalen in verschiedenen Formen und Figuren ermöglicht es uns also, verschiedene Berechnungen durchzuführen und Entfernungen zu messen. Sie sind daher ein wichtiges Konzept in der Geometrie und haben praktische Anwendungen in verschiedenen Bereichen wie Architektur, Design und Ingenieurwesen.

Zusammenfassend sind Diagonalen Linien, die zwei nicht benachbarte Eckpunkte einer geometrischen Figur verbinden. Sie spielen eine wichtige Rolle in vielen Bereichen wie Mathematik, Geometrie und Architektur. Diagonalen können zur Berechnung von Längen, Flächen und Winkeln verwendet werden und tragen zur Strukturierung und Visualisierung von Formen bei. Durch ihr vielfältiges Anwendungspotenzial sind Diagonalen ein grundlegendes Konzept in der Welt der Geometrie.