Dezimalzahlen sind eine Art von Zahlen, die wir im Alltag ständig verwenden. Sie bestehen aus einer Ganzzahl und einem Bruchteil, der durch ein Dezimaltrennzeichen dargestellt wird. In diesem Artikel erfahren Sie mehr über die Eigenschaften und Verwendung von Dezimalzahlen.
- Taxipreise für 20 km: Kosten und Berechnung | Experteninterview
- Ab wann können Babys die Babybjörn Wippe bedenkenlos nutzen?
- Selber Wölfe im Live-Ticker: Spannende Spiele und Überraschungen
- Wann kommt Wednesday Staffel 2 raus? Starttermin und Besetzung
- Wie Männer mit der Auffliegen einer Affäre umgehen: Tipps und Ratschläge
Einführung in Dezimalzahlen: Definition und Eigenschaften
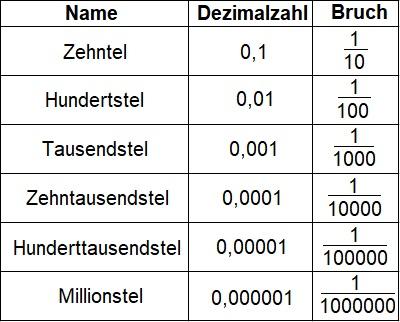
Definition von Dezimalzahlen
Dezimalzahlen sind Zahlen, die im Stellensystem mit der Basis 10 (Dezimalsystem) aufgeschrieben werden. Im Alltag und in der Schule verwenden wir meistens Dezimalzahlen. Eine Dezimalzahl kann positive oder negative Werte haben und sowohl ganze als auch gebrochene Zahlen sein.
Eigenschaften von Dezimalzahlen
– Abbrechende Dezimalzahlen: Dies sind Dezimalzahlen, die nur endlich viele Nachkommastellen haben, die nicht null sind. Sie entsprechen den Brüchen mit einer Zehnerpotenz im Nenner. Zum Beispiel ist 0,35 eine abbrechende Dezimalzahl.
– Periodische Dezimalzahlen: Bei diesen Zahlen wiederholt sich ab einer bestimmten Stelle hinter dem Komma eine Ziffer oder eine Ziffernfolge immer weiter bis ins Unendliche. Diese periodischen Zahlen werden mit einem Überstrich notiert. Zum Beispiel ist 1,1666… eine periodische Dezimalzahl.
– Irrationale Zahlen: Dies sind Dezimalzahlen, die weder abbrechen noch jemals eine Periode zeigen. Solche nicht abbrechenden und nicht periodischen Dezimalzahlen können nur angenähert aufgeschrieben werden.
– Betrag einer Zahl: Der Betrag einer Zahl gibt den Abstand der Zahl zum Nullpunkt auf der Zahlengeraden an. Der Betrag einer positiven Zahl ist einfach die Zahl selbst, während der Betrag einer negativen Zahl das Vorzeichen entfernt und sie positiv macht.
Es gibt noch weitere Eigenschaften und Begriffe im Zusammenhang mit Dezimalzahlen, aber diese grundlegenden Definitionen und Eigenschaften sollten dir helfen, ein besseres Verständnis für Dezimalzahlen zu entwickeln.
Arten von Dezimalzahlen: Abbrechend, periodisch und irrational
Arten von Dezimalzahlen: Abbrechend, periodisch und irrational
Dezimalzahlen können in verschiedene Arten unterteilt werden, je nachdem, ob sie abbrechend, periodisch oder irrational sind.
Abbrechende Dezimalzahlen haben nur endlich viele Nachkommastellen, die nicht null sind. Sie können als Bruchzahl dargestellt werden und entsprechen den Brüchen mit einer Zehnerpotenz im Nenner. Ein Beispiel für eine abbrechende Dezimalzahl ist 0,35, was dem Bruch \(\frac{7}{20}\) entspricht.
Periodische Dezimalzahlen wiederholen sich ab einer bestimmten Stelle hinter dem Komma immer weiter. Diese Wiederholung wird mit einem Überstrich notiert. Zum Beispiel ist \(\frac{7}{6} = 1,1\bar6\) eine periodische Dezimalzahl.
Abbrechende und periodische Dezimalzahlen sind rationale Zahlen, da sie als Brüche dargestellt werden können.
Irrationale Zahlen hingegen sind Dezimalzahlen, die weder abbrechen noch jemals eine Periode zeigen. Sie lassen sich nicht als Bruchzahl darstellen und können nur angenähert aufgeschrieben werden. Beispiele für irrationale Zahlen sind \(e\), \(\pi\) und \(\sqrt{2}\).
Der Betrag einer Zahl gibt den Abstand der Zahl von der Null auf der Zahlengeraden an. Der Betrag einer positiven Zahl ist gleich der Zahl selbst, während der Betrag einer negativen Zahl gleich der positiven Form dieser Zahl ist. Der Betrag einer Zahl kann mit Hilfe der Betragsfunktion berechnet werden.
Insgesamt gibt es also verschiedene Arten von Dezimalzahlen, abhängig davon, ob sie abbrechend, periodisch oder irrational sind. Der Betrag einer Zahl gibt den Abstand der Zahl von der Null an.
Darstellung von Dezimalzahlen: Zifferndarstellung und Überstrichnotation
Die Darstellung von Dezimalzahlen kann auf zwei Arten erfolgen: Zifferndarstellung und Überstrichnotation.
Bei der Zifferndarstellung werden Dezimalzahlen als eine Reihe von Ziffern dargestellt, wobei die Stellenwerte von rechts nach links zunehmen. Die erste Stelle hinter dem Komma repräsentiert den Wert \(10^{-1}\), die zweite Stelle \(10^{-2}\) usw. Jede Ziffer in der Zahl hat also einen bestimmten Stellenwert, der durch die Position bestimmt wird.
Beispiel:
Die Zahl \(123{,}45\) wird in der Zifferndarstellung als \(1 \cdot 10^2 + 2 \cdot 10^1 + 3 \cdot 10^0 + 4 \cdot 10^{-1} + 5 \cdot 10^{-2}\) dargestellt.
Bei der Überstrichnotation wiederholt sich ab einer bestimmten Stelle hinter dem Komma eine Ziffer oder eine Ziffernfolge immer weiter bis ins Unendliche. Diese wiederholte Folge wird dann mit einem Überstrich über den betreffenden Zahlen notiert.
Beispiel:
Die Zahl \(\frac{7}{6}\) wird in der Überstrichnotation als \(1{,}1\bar6\) dargestellt, da die Ziffernfolge „6“ ab der zweiten Stelle hinter dem Komma immer wiederholt wird.
Die Wahl zwischen Zifferndarstellung und Überstrichnotation hängt vom Kontext und persönlichen Vorlieben ab. Beide Darstellungsformen haben ihre eigenen Vorteile und Anwendungen.
Rationale Dezimalzahlen: Abbrechende und periodische Dezimalbrüche

Rationale Dezimalzahlen sind Zahlen, die im Dezimalsystem mit der Basis 10 geschrieben werden können. Es gibt zwei Arten von rationalen Dezimalzahlen: abbrechende und periodische Dezimalbrüche.
Abbrechende Dezimalzahlen sind solche, die nur endlich viele Nachkommastellen haben, die nicht null sind. Sie entsprechen den Dezimalbrüchen, also den Brüchen mit einer Zehnerpotenz im Nenner. Ein Beispiel für eine abbrechende Dezimalzahl ist 0,35, was dem Bruch 7/20 entspricht.
Periodische Dezimalzahlen hingegen wiederholen sich ab einer bestimmten Stelle hinter dem Komma immer weiter. Diese Wiederholung wird mit einem Überstrich notiert. Zum Beispiel entspricht die periodische Dezimalzahl 1,1666… dem Bruch 7/6.
Beide Arten von rationalen Dezimalzahlen sind Teil der Menge der rationalen Zahlen, da sie als Brüche dargestellt werden können. Irrationale Zahlen hingegen sind solche Dezimalzahlen, die weder abbrechen noch jemals eine Periode zeigen.
Es ist wichtig zu beachten, dass nicht alle dezimalen Darstellungen von rationalen Zahlen abbrechend oder periodisch sein müssen. Einige rationale Zahlen können auch in nicht-terminierender und nicht-periodischer Form dargestellt werden. In diesem Fall kann die dezimale Darstellung nur approximiert werden und ist nicht exakt.
In der Mathematik wird oft der Begriff „Dezimalbruch“ anstelle von „Dezimalzahl“ verwendet, um klar zwischen den beiden Arten von rationalen Dezimalzahlen zu unterscheiden. Abbrechende Dezimalzahlen werden als Dezimalbrüche bezeichnet, während periodische Dezimalzahlen als periodische Dezimalbrüche bezeichnet werden.
Der Betrag einer Zahl ist der positive Wert dieser Zahl, unabhängig davon, ob sie negativ oder positiv ist. Der Betrag einer Zahl wird durch das Symbol „|“ um die Zahl herum dargestellt. Zum Beispiel ist der Betrag von -5 gleich 5 und der Betrag von 7 gleich 7.
Insgesamt sind rationale Dezimalzahlen ein wichtiger Teil der Mathematik und haben viele Anwendungen in verschiedenen Bereichen wie Finanzen, Wissenschaft und Technik.
Irrationale Dezimalzahlen: Nicht abbrechende und nicht periodische Zahlen
Irrationale Dezimalzahlen sind Zahlen, die weder abbrechen noch eine sich wiederholende Periode haben. Das bedeutet, dass sie keine endliche oder periodische Darstellung haben. Stattdessen gehen diese Zahlen ins Unendliche und lassen sich nicht genau darstellen.
Ein bekanntes Beispiel für eine irrationale Dezimalzahl ist die Zahl Pi (\(\pi\)). Diese Zahl hat unendlich viele Nachkommastellen, die sich nicht wiederholen. Eine Näherung von Pi ist 3,14159…, aber dies ist nur eine Annäherung und nicht exakt.
Eine weitere bekannte irrationale Dezimalzahl ist die Wurzel aus 2 (\(\sqrt{2}\)). Auch diese Zahl hat unendlich viele Nachkommastellen, die sich nicht wiederholen lassen. Eine Näherung von \(\sqrt{2}\) ist 1,41421…, aber auch hier handelt es sich um eine Annäherung.
Irrationale Dezimalzahlen sind wichtige Konzepte in der Mathematik und spielen eine Rolle in vielen Bereichen wie Geometrie und Analysis. Sie zeigen uns, dass es Zahlen gibt, die nicht durch Brüche oder endliche Dezimaldarstellungen dargestellt werden können.
Der Betrag einer Zahl: Absolute Wertbestimmung bei positiven und negativen Zahlen
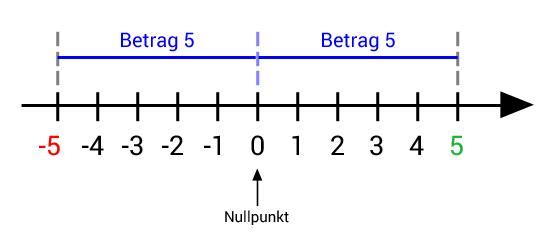
Der Betrag einer Zahl ist ein mathematischer Ausdruck, der den Abstand dieser Zahl von der Null auf einer Zahlenlinie beschreibt. Er gibt an, wie weit eine Zahl von null entfernt ist, unabhängig davon, ob sie positiv oder negativ ist. Der Betrag einer Zahl wird oft durch zwei senkrechte Striche um die Zahl herum dargestellt.
Für positive Zahlen entspricht der Betrag einfach der Zahl selbst. Zum Beispiel ist der Betrag von 5 gleich 5.
Für negative Zahlen wird der Betrag durch das Entfernen des Vorzeichens bestimmt. Dies bedeutet, dass der Betrag einer negativen Zahl immer positiv ist. Zum Beispiel ist der Betrag von -3 gleich 3.
Der Betrag einer Zahl kann auch als absolute Wertbestimmung bezeichnet werden. Es handelt sich um eine Funktion, die jede reelle Zahl auf ihre positive Entsprechung abbildet.
Um den Betrag einer Zahl zu berechnen, muss man das Vorzeichen ignorieren und nur den numerischen Wert betrachten. Der resultierende Wert ist immer nicht-negativ.
Der Betrag einer Zahl kann in verschiedenen mathematischen Bereichen verwendet werden, zum Beispiel bei Ungleichungen oder beim Lösen von Gleichungen mit absoluten Werten.
Zusammenfassend lässt sich sagen, dass der Betrag einer Zahl den Abstand dieser Zahl von null beschreibt und unabhängig vom Vorzeichen immer einen nicht-negativen Wert ergibt.
Dezimalzahlen sind Zahlen, die im Dezimalsystem dargestellt werden und eine Nachkommastelle haben können. Sie spielen eine wichtige Rolle in der Mathematik und im Alltag, da sie uns ermöglichen, genaue Messungen und Berechnungen durchzuführen. Dezimalzahlen können positiv oder negativ sein und werden oft mit Kommazahlen oder Brüchen in Beziehung gesetzt. Ein Verständnis für Dezimalzahlen ist daher unerlässlich, um mathematische Probleme zu lösen und Informationen präzise darzustellen.

