Was sind Pseudotetraden im BCD-Code?

Pseudotetraden im BCD-Code sind eine besondere Art von Zahlenkombinationen. In diesem kurzen Einführungstext werden wir erklären, was Pseudotetraden sind und wie sie im BCD-Code verwendet werden.

Die Bedeutung von Pseudotetraden im BCD-Code

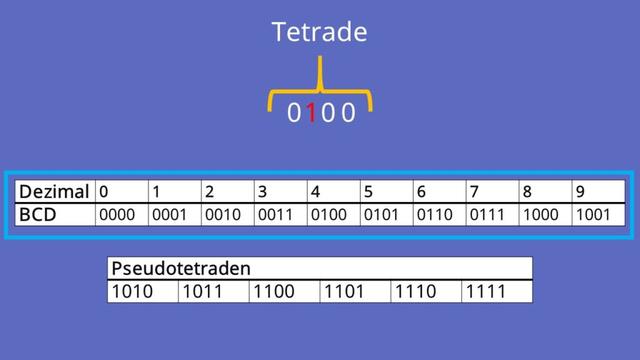
Die Pseudotetraden im BCD-Code haben keine Funktion und gehören nicht zu den eigentlichen Tetraden. Sie werden auch nicht im BCD-Code verwendet oder dürfen nicht auftreten. Insgesamt werden für die 10 Dezimalziffern nur 10 Tetraden benötigt. Die übrigen 6 Tetraden sind Pseudotetraden.

Im BCD-Code wird jede Dezimalziffer durch eine eigene 4-Bit-Dualzahl bzw. binären Code dargestellt. Eine Tetrade besteht aus 4 Bits, die eine Vierergruppe bilden. Für eine dreistellige Dezimalzahl von 0 bis 999 benötigt man als Dualzahl 10 Bit (1111100111). Als binär codierte Dezimalzahl benötigt man jedoch 12 Bit (0011 1110 0111 BCD).

Da der BCD-Code relativ verschwenderisch ist und der Speicher zu stark genutzt wird, werden in der Praxis andere Codes verwendet. Diese sind effizienter und sparsamer im Umgang mit dem Speicher. Die BCD-Arithmetik wird daher nur noch selten angewendet.

Allerdings gibt es immer noch Bereiche wie das Finanzwesen und die Wissenschaft, in denen eine sehr hohe Genauigkeit gefordert ist, die über die Gleitkommadarstellung hinausgeht. Hier kommen spezielle Codierungen wie das Densely Packed Decimal Encoding zum Einsatz.

In der Digitaltechnik und bei digitalen Anzeigen findet die BCD-Codierung Verwendung. Zum Beispiel werden Digitaluhren im Inneren mit dem BCD-Code betrieben und auch die Uhrzeit im DCF77-Signal ist als BCD-Code kodiert.

Um den 4-Bit-Dualcode als Dezimalzahl anzeigen zu können, wird ein BCD-Decoder und eine 7-Segment-Anzeige verwendet. Der BCD-Decoder wandelt den BCD-Code auf die 7 Segmente um, die wiederum die Dezimalziffern darstellen.

Die Elektronik-Fibel ist ein Buch, das sich mit den Grundlagen der Elektronik, Bauelementen, Schaltungstechnik und Digitaltechnik beschäftigt. Sie bietet eine einfache und verständliche Erklärung dieser Themen und ist besonders für Auszubildende geeignet.

Zusätzlich zum Buch kann man auch einen Online-Workshop zum Elektronik-Set buchen. Diese Workshops sind praxisorientiert und bieten eine fundierte Einarbeitung in die Elektronik.

Kundenmeinungen zu der Elektronik-Fibel sind sehr positiv. Ein Kunde bezeichnet sie als genial und lobt ihre Einfachheit und Verständlichkeit. Ein anderer Kunde gibt an, dass er sich mit dem Timer-Buch viel Zeit gespart hätte, wenn er es früher gehabt hätte.

Das Elektronik-Set enthält unter anderem ein Steckbrett mit 400 Kontakten, Verbindungskabel zum Stecken, einen Batterie-Clip für einen 9-Volt-Block sowie einen Micro-USB-Adapter für ein USB-Netzteil. Damit kann man ohne Lötkolben experimentieren und Bauteile einfach stecken.

Verwendung und Funktion von Pseudotetraden im BCD-Code

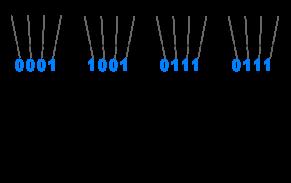
Im BCD-Code werden 10 Tetraden verwendet, um die Dezimalziffern 0 bis 9 darzustellen. Die restlichen 6 Tetraden werden als Pseudotetraden bezeichnet und haben keine Funktion im BCD-Code. Sie sind überflüssig und treten nicht auf.

Der Grund für die Verwendung von Pseudotetraden liegt darin, dass die binäre Darstellung einer dreistelligen Dezimalzahl mit dem BCD-Code 10 Bit benötigen würde. Da dies relativ ineffizient ist, werden in der Praxis andere Codes verwendet, die sparsamer sind.

Die BCD-Arithmetik wird heutzutage nur noch selten angewendet, da der Speicher zu verschwenderisch genutzt wird. Zudem bieten BCD-Zahlen im Vergleich zu 32-Bit-Gleitkommazahlen nur eine geringfügig höhere Genauigkeit.

Allerdings gibt es immer noch Anwendungsgebiete wie das Finanzwesen und die Wissenschaft, in denen eine sehr hohe Genauigkeit gefordert ist. Hier kommen spezielle Codierungen wie das Densely Packed Decimal Encoding zum Einsatz.

In der Digitaltechnik und bei digitalen Anzeigen findet die BCD-Codierung Verwendung. Zum Beispiel werden Digitaluhren im Innern mit dem BCD-Code betrieben. Auch die Uhrzeit im DCF77-Signal wird als BCD-Code kodiert.

Um den 4-Bit-Dualcode als Dezimalzahl anzeigen zu können, wird ein BCD-Decoder und eine 7-Segment-Anzeige verwendet. Der Decoder wandelt den BCD-Code in die entsprechenden Signale für die 7 Segmente um, sodass die Dezimalzahl angezeigt werden kann.

Die Elektronik-Fibel ist ein Buch, das grundlegende Informationen über Elektronik, Bauelemente, Schaltungstechnik und Digitaltechnik vermittelt. In Kombination mit dem Elektronik-Set Starter Edition bietet der Online-Workshop eine praxisorientierte Einführung in die Elektronik.

Kundenmeinung: „Die Elektronik-Fibel ist einfach genial. Sie ist leicht verständlich und enthält alles, was man als Azubi braucht. Danke für dieses großartige Werk.“

Das Elektronik-Set Starter Edition beinhaltet ein Steckbrett mit 400 Kontakten, Verbindungskabel zum Stecken, einen Batterie-Clip für einen 9-Volt-Block und einen Micro-USB-Adapter für ein USB-Netzteil.

Kundenmeinung: „Hätte ich das Timer-Buch schon früher gehabt, dann hätte ich mir die Rumfrickelei am NE555 sparen können.“

Mit der Elektronik-Fibel erhält man schnell ein Verständnis für Bauteile und Schaltsymbole. Zudem ermöglicht das Set Experimente ohne Lötkolben, da die Bauteile einfach gesteckt werden können.

Der 8-4-2-1-BCD-Code und seine Pseudotetraden

Was ist der 8-4-2-1-BCD-Code?

Der 8-4-2-1-BCD-Code, auch bekannt als Binary Coded Decimals (binär-kodierte Dezimalziffern), ist ein Code zur digitalen Darstellung und Verarbeitung von Zahlen. Es handelt sich um dualkodierte Zahlen, bei denen jede Dezimalziffer durch 4 Bit der entsprechenden dualen Zahl dargestellt wird. Die Bezeichnung „8-4-2-1“ bezieht sich auf die dezimale Wertigkeit der dualen Stellen im Code.

Wie funktioniert der 8-4-2-1 BCD Code?

Für jede Dezimalziffer einer Dezimalzahl wird eine eigene 4-Bit-Dualzahl bzw. binärer Code verwendet. Diese 4 Bit werden auch als Tetrade bezeichnet. Insgesamt werden für die zehn Dezimalziffern nur zehn Tetraden benötigt. Die restlichen sechs Tetraden werden Pseudotetraden genannt und haben keine Funktion im BCD-Code.

Warum wird der BCD Code nicht häufig verwendet?

In der Praxis werden oft andere Codes verwendet, da der BCD Code zu verschwenderisch im Speicher ist. Für eine dreistellige Dezimalzahl von 0 bis 999 würde man beispielsweise 12 Bit benötigen. Im Vergleich dazu bieten andere Codes eine effizientere Nutzung des Speichers. Zudem liefern BCD-Zahlen gegenüber 32-Bit-Gleitkommazahlen nur eine geringfügig höhere Genauigkeit. Dennoch gibt es im Finanzwesen und in der Wissenschaft weiterhin Bedarf an einer sehr hohen Genauigkeit, die über die Gleitkommadarstellung hinausgeht.

Verwendung des BCD-Codes

Der BCD-Code wird in der Digitaltechnik und bei digitalen Anzeigen eingesetzt. Beispielsweise werden Digitaluhren im Inneren mit dem BCD-Code betrieben. Auch die Uhrzeit im DCF77-Signal wird als BCD-Code kodiert. Um den 4-Bit-Dualcode als Dezimalzahl anzeigen zu können, wird ein BCD-Decoder und eine 7-Segment-Anzeige verwendet. Die 7-Segment-Anzeige besteht aus sieben Leuchtstreifen, die wie ein „8“ angeordnet sind. Der BCD-Decoder wandelt den 4-Bit-Dualcode in die entsprechenden Signale für die Segmente um.

Insgesamt bietet der BCD-Code eine Möglichkeit zur digitalen Darstellung von Dezimalzahlen, jedoch wird er aufgrund seiner ineffizienten Speichernutzung und geringfügig höheren Genauigkeit gegenüber anderen Codes nur noch selten angewendet.

Warum Pseudotetraden im BCD-Code nicht benötigt werden

Die Verwendung von Pseudotetraden im BCD-Code ist nicht erforderlich, da sie keine Funktion haben und somit verschwendet wären. Der BCD-Code repräsentiert dezimale Zahlen durch 4-Bit-Dualzahlen, wobei jede Dezimalziffer ihre eigene 4-Bit-Dualzahl hat. Für die 10 Dezimalziffern werden nur 10 Tetraden benötigt, während die übrigen 6 Tetraden als Pseudotetraden bezeichnet werden.

In der Praxis werden diese Pseudotetraden nicht verwendet, da sie keinen Nutzen haben und den Speicherplatz unnötig beanspruchen würden. Stattdessen werden andere Codes verwendet, die effizienter sind. Die BCD-Arithmetik wird heutzutage nur noch selten angewendet, da sie zu verschwenderisch mit dem Speicher umgeht.

BCD-Zahlen bieten gegenüber 32-Bit-Gleitkommazahlen nur eine geringfügig höhere Genauigkeit. In Bereichen wie dem Finanzwesen und der Wissenschaft besteht jedoch immer noch Bedarf an einer sehr hohen Genauigkeit, die über die Gleitkommadarstellung hinausgeht. Hier kommen spezielle Codierungen wie das Densely Packed Decimal Encoding zum Einsatz.

Die BCD-Codierung findet Anwendung in der Digitaltechnik und bei digitalen Anzeigen wie z.B. 7-Segment-Anzeigen. Bei Digitaluhren wird die Uhrzeit im DCF77-Signal als BCD-Code kodiert. Um den BCD-Code als Dezimalzahl anzeigen zu können, wird ein BCD-Decoder und eine 7-Segment-Anzeige verwendet. Der BCD-Decoder wandelt den 4-Bit-Dualcode in die entsprechenden Signale für die 7 Segmente um.

Insgesamt ist die Verwendung von Pseudotetraden im BCD-Code nicht erforderlich und wird daher nicht genutzt. Stattdessen werden effizientere Codes verwendet, um den Speicherplatz besser auszunutzen und eine höhere Genauigkeit zu erreichen.

Effizientere Alternativen zum BCD-Code mit Pseudotetraden

Der BCD-Code war eine Methode, um Dezimalzahlen binär zu kodieren. Dabei wurde jede Dezimalziffer durch 4 Bits dargestellt. Allerdings wurden dabei auch 6 zusätzliche Tetraden verwendet, die keine Funktion hatten und somit verschwendet wurden. Deshalb werden in der Praxis heute effizientere Alternativen zum BCD-Code eingesetzt.

Eine solche Alternative ist das Densely Packed Decimal Encoding (DPD). Dieser Code wird in einigen Computern von der Hardware unterstützt oder steht über Software-Bibliotheken zur Verfügung. Er ermöglicht eine höhere Genauigkeit als der BCD-Code und nutzt den Speicherplatz effizienter.

Ein weiterer Vorteil von DPD ist seine Verwendung im Finanzwesen und in der Wissenschaft, wo eine sehr hohe Genauigkeit benötigt wird. Im Gegensatz zu Gleitkommazahlen bieten DPD-Zahlen eine etwas höhere Genauigkeit. Daher ist die BCD-Arithmetik immer noch relevant und wird in bestimmten Bereichen eingesetzt.

In der Digitaltechnik und bei digitalen Anzeigen wie z.B. 7-Segment-Anzeigen wird die BCD-Codierung verwendet. Hierbei werden die 4-Bit-Dualzahlen mithilfe eines BCD-Decoders auf die 7 Segmente einer Anzeige umgewandelt.

Insgesamt gibt es also effizientere Alternativen zum BCD-Code mit Pseudotetraden, die in verschiedenen Bereichen eingesetzt werden können. Diese Codes ermöglichen eine höhere Genauigkeit und nutzen den Speicherplatz effizienter.

Anwendungen der BCD-Codierung und die Rolle von Pseudotetraden

Die BCD-Codierung wird in der Digitaltechnik und digitalen Anzeigen eingesetzt, wie zum Beispiel bei 7-Segment-Anzeigen. Diese Art von Anzeige besteht aus 7 Leuchtstreifen, die wie ein „8“ angeordnet sind. Um die 4-Bit-Dualzahl als Dezimalzahl auf der 7-Segment-Anzeige anzeigen zu können, verwendet man einen BCD-Decoder. Dieser decodiert den BCD-Code (4-Bit) auf die 7 Segmente um.

Auch Digitaluhren verwenden im Inneren den BCD-Code zur Darstellung der Uhrzeit. Das DCF77-Signal, das die Uhrzeit überträgt, ist ebenfalls als BCD-Code kodiert.

Die Rolle von Pseudotetraden ist interessant. Für die 10 Dezimalziffern werden nur 10 Tetraden benötigt. Die restlichen 6 Tetraden werden Pseudotetraden genannt und haben keine Funktion mehr. Sie treten im BCD-Code nicht auf bzw. dürfen nicht auftreten.

In der Praxis werden jedoch andere Codes verwendet, da der BCD-Code zu verschwenderisch mit Speicher umgeht. Die BCD-Arithmetik wird daher nur noch selten angewendet. Außerdem bieten BCD-Zahlen gegenüber 32-Bit-Gleitkommazahlen nur eine etwas höhere Genauigkeit.

Allerdings gibt es immer noch Bedarf für eine sehr hohe Genauigkeit in Bereichen wie dem Finanzwesen und der Wissenschaft, welche über die Gleitkommadarstellung hinausgeht. Hier kommen spezielle Codierungen wie das Densely Packed Decimal Encoding zum Einsatz, das auf manchen Rechnern von der Hardware unterstützt wird oder über Software-Bibliotheken verfügbar ist. Diese Codierungen werden sowohl in Großrechnern als auch in technisch-wissenschaftlichen Taschenrechnern verwendet.

Insgesamt hat die BCD-Codierung eine wichtige Rolle in der Digitaltechnik und findet Anwendung in verschiedenen Bereichen, insbesondere bei der Darstellung von Zahlen auf digitalen Anzeigen.

Zusammenfassend kann gesagt werden, dass Pseudotetraden im BCD-Code eine Methode zur Darstellung von Zahlen ist, bei der vier Bit als eine Gruppe betrachtet werden. Diese Technik ermöglicht die effiziente Codierung und Decodierung von Dezimalzahlen im binären System. Durch die Verwendung von Pseudotetraden können komplexe Rechenoperationen vereinfacht und Speicherplatz eingespart werden.