Was ist eine Nullstelle und wie findet man sie?

Eine Nullstelle ist ein mathematischer Begriff, der den Punkt oder die Punkte auf einer Funktion beschreibt, an denen der Funktionswert gleich null ist. In diesem Artikel werden wir genauer darauf eingehen, was eine Nullstelle ist und wie sie in der Mathematik verwendet wird.

Was ist eine Nullstelle und wie findet man sie?

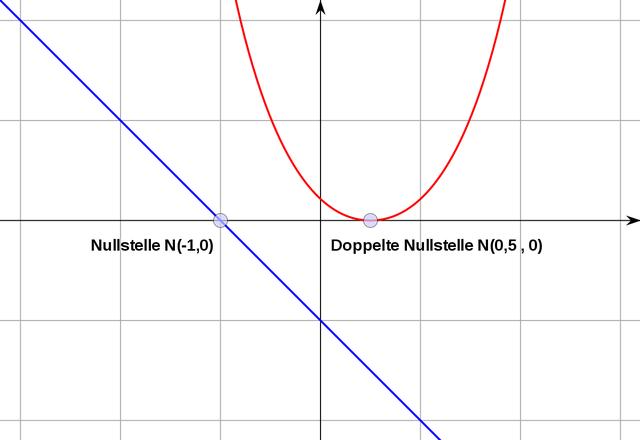
Eine Nullstelle ist der Wert für x, bei dem die Funktion den y-Wert 0 hat. Es ist der Punkt auf der x-Achse, an dem der Graph einer Funktion diese Achse schneidet. Die Nullstelle gibt also den Zeitpunkt oder den Wert an, bei dem die Funktion einen y-Wert von 0 erreicht.

Um die Nullstellen einer linearen Funktion zu finden, setzt man die Funktion gleich 0 und löst nach x auf. Dazu kann man verschiedene mathematische Methoden verwenden, wie beispielsweise das Umstellen der Gleichung oder das Anwenden von Rechenregeln.

Für lineare Funktionen in der Form f(x) = mx + b kann man die Nullstelle mit der Formel x = -b/m berechnen. Dabei darf m nicht gleich 0 sein.

Es ist auch möglich, die Nullstellen zeichnerisch zu ermitteln, indem man den Graphen der Funktion betrachtet und die Stellen abliest, an denen er die x-Achse schneidet.

Es ist wichtig zu beachten, dass nicht alle Funktionen genau eine Nullstelle haben. Manche Funktionen können mehrere Nullstellen haben oder auch gar keine, zum Beispiel wenn die Steigung m gleich 0 ist und der Graph parallel zur x-Achse verläuft.

Das Lernportal von kapiert.de bietet eine umfangreiche Unterstützung beim Verständnis und bei der Berechnung von Nullstellen. Mit Videos, Audios und Grafiken wird das Thema anschaulich erklärt und mit interaktiven Übungen kann man das Gelernte direkt anwenden. Der Klassenarbeitstrainer hilft dabei, sich gezielt auf Klausuren vorzubereiten, und der Lernmanager ermöglicht einen Überblick über alle Aufgaben. Teste das Lernportal von kapiert.de jetzt drei Tage kostenlos!

Die Bedeutung und Berechnung von Nullstellen in linearen Funktionen

Die Bedeutung von Nullstellen

Nullstellen sind die x-Werte einer Funktion, bei denen der y-Wert 0 ist. In Bezug auf lineare Funktionen geben sie den Zeitpunkt oder den Punkt an, an dem die Funktion den Wert 0 erreicht. Im gegebenen Beispiel der Kerzenlänge bedeutet die Nullstelle, dass die Kerze abgebrannt ist und ihre Länge 0 beträgt. Der zugehörige Punkt (6|0) liegt auf der x-Achse.

Berechnung von Nullstellen

Um die Nullstelle einer linearen Funktion zu berechnen, setzt man die Funktion gleich 0 und löst nach x auf. Im gegebenen Beispiel lautet die Funktionsgleichung f(x) = -3x + 18. Um die Nullstelle zu ermitteln, setzen wir f(x) = 0:

-3x + 18 = 0

Um x zu isolieren, subtrahieren wir 18 von beiden Seiten:

-3x = -18

Teilen wir nun beide Seiten durch -3:

x = 6

Die Nullstelle dieser linearen Funktion ist also x = 6. Dies bedeutet, dass die Kerze nach 6 Stunden abgebrannt ist.

Zusammenfassend lässt sich sagen, dass Nullstellen in linearen Funktionen den Zeitpunkt oder Punkt angeben, an dem der y-Wert der Funktion den Wert 0 erreicht. Sie können durch das Lösen der Gleichung f(x) = 0 bestimmt werden.

Wie ermittelt man die Nullstellen einer Funktion?

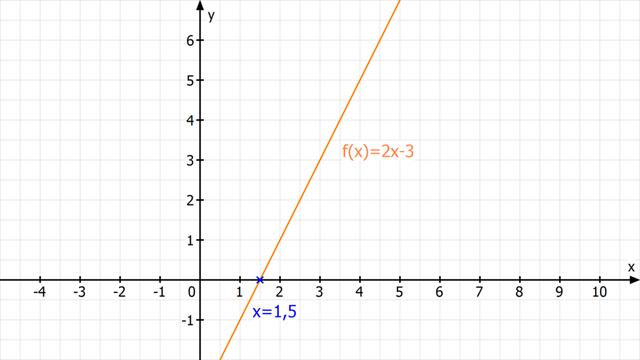
Definition der Nullstelle

Die Nullstelle einer Funktion ist der Wert für x, bei dem die Funktion den y-Wert 0 hat. Es ist der Punkt auf der x-Achse, an dem der Funktionsgraph die x-Achse schneidet.

Berechnung der Nullstellen

Um die Nullstellen einer Funktion zu ermitteln, setzt man die Funktion gleich 0 und löst nach x auf. Dabei können verschiedene Methoden angewendet werden, wie zum Beispiel das Umformen der Gleichung oder das Anwenden von Lösungsverfahren wie dem Einsetzungsverfahren oder dem Ausklammern.

Beispiel:
Gegeben sei die lineare Funktion f(x) = -3x + 18. Um die Nullstelle zu finden, setzen wir f(x) = 0 und lösen nach x auf:

-3x + 18 = 0
-3x = -18
x = -18 / -3
x = 6

Die Nullstelle dieser Funktion ist also x = 6.

Graphische Ermittlung der Nullstellen

Eine weitere Möglichkeit, die Nullstellen einer Funktion zu ermitteln, besteht darin, den Graphen der Funktion zu zeichnen und die Schnittpunkte mit der x-Achse abzulesen. Die Schnittpunkte mit der x-Achse entsprechen den Nullstellen.

Es ist wichtig zu beachten, dass eine lineare Funktion immer genau eine Nullstelle hat, außer wenn ihre Steigung m gleich 0 ist. In diesem Fall verläuft der Graph parallel zur x-Achse und schneidet diese nicht.

Das Ermitteln der Nullstellen einer Funktion ist ein wichtiger Schritt bei der Analyse von Funktionen und kann dabei helfen, bestimmte Eigenschaften und Verhaltensweisen der Funktion zu verstehen.

Das Konzept der Nullstellen in Mathematik erklärt

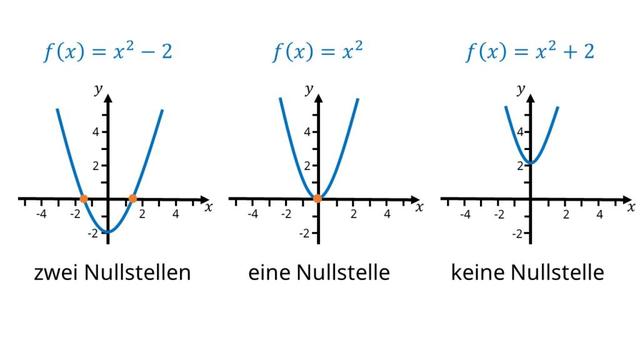
Was sind Nullstellen?

Nullstellen sind die $$x$$-Werte einer Funktion, bei denen der $$y$$-Wert gleich null ist. In anderen Worten, es sind die Punkte auf dem Graphen einer Funktion, an denen sie die $$x$$-Achse schneidet.

Wie findet man Nullstellen?

Um die Nullstellen einer Funktion zu finden, setzt man den $$y$$-Wert gleich null und löst nach $$x$$ auf. Das bedeutet, dass man den Wert von $$x$$ bestimmt, bei dem die Funktion den Wert null annimmt.

Beispiel: Gegeben sei die lineare Funktion $$f(x) = -3x + 18$$. Um die Nullstelle zu finden, setzen wir $$f(x)$$ gleich null und lösen nach $$x$$ auf:
$$-3x + 18 = 0$$
Durch Umformung erhalten wir:
$$-3x = -18$$
Teilen wir nun beide Seiten der Gleichung durch -3, erhalten wir:
$$x = 6$$

Die Nullstelle dieser Funktion ist also $$x=6$$. Das bedeutet, dass die Kerze nach 6 Stunden abgebrannt ist.

Zeichnerische Bestimmung der Nullstellen

Man kann auch graphisch bestimmen, wo eine Funktion die $$x$$-Achse schneidet. Die Schnittpunkte mit der $$x$$-Achse entsprechen den Nullstellen der Funktion.

Wenn man den Graphen einer Funktion zeichnet, kann man die Stelle ablesen, an der er die $$x$$-Achse schneidet. Dieser $$x$$-Wert ist dann die Nullstelle der Funktion.

Es ist wichtig zu beachten, dass eine lineare Funktion immer genau eine Nullstelle hat, außer wenn die Steigung der Funktion gleich null ist. In diesem Fall verläuft der Graph parallel zur $$x$$-Achse und schneidet sie nicht.

Das Konzept der Nullstellen ist ein grundlegendes Konzept in der Mathematik und wird in vielen Bereichen angewendet, wie zum Beispiel bei der Lösung von Gleichungen oder bei der Analyse von Funktionen.

Die Suche nach den Schnittpunkten mit der x-Achse: Was sind Nullstellen?

Was sind Nullstellen?

Nullstellen sind die x-Werte einer Funktion, bei denen der y-Wert 0 ist. Sie geben also die Stellen an, an denen der Graph einer Funktion die x-Achse schneidet.

– Eine Nullstelle ist der Zeitpunkt oder Wert, bei dem eine bestimmte Bedingung erfüllt ist.
– Bei linearen Funktionen entspricht die Nullstelle dem x-Wert, für den f(x) = 0 gilt.
– Die Nullstelle gibt den Zeitpunkt oder Wert an, bei dem eine Funktion ihren Ausgangswert erreicht oder durchquert.
– Um die Nullstelle einer linearen Funktion zu berechnen, setzt man f(x) = 0 und löst nach x auf.

Beispiel:
Die Kerze ist zu Beginn 18 cm lang und brennt pro Stunde um 3 cm ab. Wir suchen den Zeitpunkt, an dem die Kerze abgebrannt ist.

Die Funktionsgleichung für die Kerzenlänge lautet f(x) = -3x + 18. Um herauszufinden, wann die Kerze abgebrannt ist (also wenn f(x) = 0), setzen wir -3x + 18 = 0 und lösen nach x auf:

-3x + 18 = 0
-3x = -18
x = 6

Die Nullstelle dieser linearen Funktion liegt also bei x = 6. Das bedeutet, dass die Kerze nach 6 Stunden abgebrannt ist.

Der Schnittpunkt mit der x-Achse wird durch den Punkt (6|0) dargestellt. Dieser Punkt liegt auf der x-Achse, da der y-Wert 0 ist.

Zusammenfassend können wir sagen, dass die Nullstelle einer Funktion die Stelle ist, an der der Graph die x-Achse schneidet und der y-Wert gleich 0 ist. In unserem Beispiel war dies nach 6 Stunden der Fall.

Lineare Funktionen: Wie finde ich die Stelle, an der f(x) = 0 ist?

Die Nullstelle einer linearen Funktion finden

– Eine Nullstelle ist eine Stelle, an der die Funktion den y-Wert 0 hat. Um die Nullstelle einer linearen Funktion zu finden, setzen wir f(x) = 0.
– In unserem Beispiel betrachten wir eine Kerze, deren Länge mit der Zeit abnimmt. Die Funktionsgleichung für die Kerzenlänge lautet f(x) = -3x + 18.
– Um herauszufinden, wann die Kerze abgebrannt ist (also wenn ihre Länge 0 beträgt), setzen wir f(x) = 0 und lösen nach x auf.
– Für unsere Funktion ergibt sich folgende Gleichung: -3x + 18 = 0.
– Durch Umstellen der Gleichung erhalten wir x = 6. Das bedeutet, dass die Kerze nach 6 Stunden abgebrannt ist.

Der Schnittpunkt mit der x-Achse

– Der Schnittpunkt mit der x-Achse ist der Punkt, an dem die Funktion den y-Wert 0 hat.
– In unserem Beispiel liegt dieser Punkt bei (6 | 0). Das bedeutet, dass nach 6 Stunden die Kerze abgebrannt ist und ihre Länge 0 beträgt.

Zeichnerisches Ermitteln der Nullstellen

– Um die Nullstellen einer linearen Funktion zeichnerisch zu ermitteln, suchen wir nach den Schnittpunkten des Graphen mit der x-Achse.
– Alle Punkte auf der x-Achse haben die y-Koordinate 0.
– Der Schnittpunkt eines Graphen mit der x-Achse ergibt sich aus der Nullstelle als x-Wert und dem zugehörigen y-Wert 0: S(x | 0).
– In unserem Beispiel beträgt die Nullstelle x = 6, also liegt der Schnittpunkt mit der x-Achse bei S(6 | 0).

Zusammenfassung

– Die Nullstelle einer linearen Funktion ist die Stelle, an der die Funktion den y-Wert 0 hat.
– Um die Nullstelle zu finden, setzen wir f(x) = 0 und lösen nach x auf.
– Der Schnittpunkt mit der x-Achse ist der Punkt, an dem die Funktion den y-Wert 0 hat. Dieser Punkt wird als S(x | 0) bezeichnet.
– Die Nullstellen einer linearen Funktion können auch zeichnerisch ermittelt werden, indem man nach den Schnittpunkten des Graphen mit der x-Achse sucht.

Teste jetzt das Lernportal von kapiert.de drei Tage lang kostenlos! Mit Videos, Audios und Grafiken erklären wir dir jedes Thema. Nutze den Klassenarbeitstrainer, um dich optimal auf deine Mathe-Klausur vorzubereiten. Mit dem Lernmanager behältst du alle Aufgaben im Blick.

In der Mathematik ist eine Nullstelle einer Funktion der Wert, bei dem die Funktion den Wert null annimmt. Nullstellen sind wichtige Punkte, um das Verhalten und die Eigenschaften einer Funktion zu analysieren. Sie ermöglichen es uns, Gleichungen zu lösen und Schnittpunkte mit der x-Achse zu bestimmen. Durch das Finden von Nullstellen können wir auch Symmetrieachsen und Extrempunkte identifizieren.