Eine irrationale Zahl, auch als „Nichtverhältniszahl“ bekannt, ist eine Zahl, deren Dezimaldarstellung weder periodisch noch abbrechend ist. Im Gegensatz zu rationalen Zahlen können sie nicht als Bruch zweier ganzer Zahlen dargestellt werden. Irrationale Zahlen spielen eine wichtige Rolle in der Mathematik und haben faszinierende Eigenschaften. In diesem Artikel werden wir uns näher mit dem Konzept irrationaler Zahlen befassen und ihre Bedeutung untersuchen.
Erklärung und Beispiele: Was ist eine irrationale Zahl?
Definition einer irrationalen Zahl
Eine irrationale Zahl ist eine reelle Zahl, die nicht als Bruch zweier ganzer Zahlen dargestellt werden kann. Anders ausgedrückt, sie lässt sich nicht als Verhältnis von zwei ganzen Zahlen darstellen. Irrationale Zahlen haben unendlich viele Dezimalstellen, die weder periodisch noch abbrechend sind.
Beispiele für irrationale Zahlen
Ein bekanntes Beispiel für eine irrationale Zahl ist die Kreiszahl Pi (π). Pi ist definiert als das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser und hat unendlich viele Dezimalstellen ohne ein erkennbares Muster. Eine andere bekannte irrationale Zahl ist die Eulersche Zahl e, die in vielen mathematischen Zusammenhängen verwendet wird.
Weitere Beispiele für irrationale Zahlen sind die Quadratwurzel von 2 (√2), die goldene Zahl φ (Phi) und die Wurzel aus 3 (√3). Diese Zahlen lassen sich nicht exakt als Bruch zweier ganzer Zahlen darstellen und haben unendlich viele nicht-periodische Dezimalstellen.
Es gibt unendlich viele irrationalen Zahlen, da zwischen jeder zwei rationalen Zahlen immer eine irrationalen Zahl existiert. Irrationale Zahlen sind ein wichtiger Bestandteil der Mathematik und haben vielfältige Anwendungen sowohl in der Theorie als auch in der Praxis.
Die Bedeutung irrationaler Zahlen: Eine Einführung
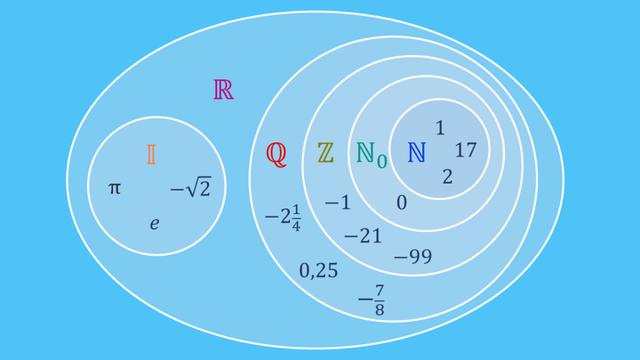
Was sind rationale und irrationale Zahlen?
Rationale Zahlen sind Zahlen, die als Bruch dargestellt werden können. Das bedeutet, dass sie entweder als ganzer Zahl, als Dezimalzahl oder als endlicher oder periodischer Bruch geschrieben werden können. Beispiele für rationale Zahlen sind 1, -5, 0, 0.25 und ⅔.
Im Gegensatz dazu sind irrationale Zahlen Zahlen, die nicht als Bruch darstellbar sind. Sie haben unendlich viele Nachkommastellen und keine wiederkehrende Periodizität. Ein bekanntes Beispiel für eine irrationale Zahl ist die Kreiszahl Pi (π), die ungefähr 3,14159… lautet.
Die Bedeutung irrationaler Zahlen
Irrationale Zahlen spielen eine wichtige Rolle in der Mathematik. Sie erweitern den Zahlenbereich der rationalen Zahlen und ermöglichen es uns, mathematische Probleme genauer zu lösen. Zum Beispiel werden irrationalen Zahlen verwendet, um Längen von Seiten in rechtwinkligen Dreiecken genau zu berechnen oder den Flächeninhalt von Kreisen exakt zu bestimmen.
Darüber hinaus haben irrationale Zahlen auch eine tiefere philosophische Bedeutung. Sie zeigen uns, dass es in der Mathematik unendlich viele verschiedene Arten von Zahlen gibt und dass die Welt der Mathematik komplexer ist als wir es uns vielleicht vorstellen können.
Insgesamt tragen rationale und irrationale Zahlen dazu bei, unser Verständnis von Mathematik zu erweitern und ermöglichen es uns, komplexe Probleme präziser zu lösen. Sie sind ein grundlegender Bestandteil der Mathematik und werden in vielen Bereichen wie Geometrie, Physik und Ingenieurwesen angewendet.
Irrationale Zahlen verstehen: Definition und Anwendung
Definition irrationaler Zahlen
Irrationale Zahlen sind eine spezielle Art von reellen Zahlen, die nicht als Bruch zweier ganzer Zahlen dargestellt werden können. Im Gegensatz zu rationalen Zahlen, die als Verhältnis zweier ganzer Zahlen darstellbar sind, haben irrationale Zahlen unendlich viele Dezimalstellen ohne periodisches Muster. Bekannte Beispiele für irrationale Zahlen sind die Wurzeln von Nicht-Quadratzahlen wie √2 oder π (Pi).
Anwendung irrationaler Zahlen
Irrationale Zahlen finden in verschiedenen Bereichen der Mathematik und Naturwissenschaften Anwendung. In der Geometrie spielen sie eine wichtige Rolle bei der Konstruktion von Längenverhältnissen, zum Beispiel bei der Konstruktion des goldenen Schnitts. In der Physik werden irrationale Zahlen verwendet, um Naturkonstanten wie die Lichtgeschwindigkeit oder den Planckschen Wirkungsquantum exakt zu berechnen.
Die Kenntnis irrationaler Zahlen ist auch im Alltag relevant. Zum Beispiel beim Umrechnen von Einheiten oder dem Berechnen von Flächeninhalten oder Volumina. Irrationale Zahlen ermöglichen präzise Messungen und genaue Berechnungen in vielen Anwendungsgebieten.
Insgesamt sind rationale und irrationale Zahlen grundlegende Konzepte in der Mathematik, die sowohl theoretisch als auch praktisch von großer Bedeutung sind. Durch das Verständnis dieser Zahlentypen können komplexe mathematische Probleme gelöst und mathematische Modelle in verschiedenen Bereichen angewendet werden.
Irrationale Zahlen kennenlernen: Wichtige Informationen im Überblick
Was sind irrationale Zahlen?
Irrationale Zahlen sind Zahlen, die nicht als Bruch zweier ganzer Zahlen dargestellt werden können. Sie haben unendlich viele Dezimalstellen, die weder periodisch noch abbrechend sind. Ein bekanntes Beispiel für eine irrationale Zahl ist die Kreiszahl Pi (π). Irrationale Zahlen werden oft durch Symbole wie √2 oder e dargestellt.
Warum sind irrationale Zahlen wichtig?
Das Konzept irrationaler Zahlen ist von großer Bedeutung in der Mathematik. Durch das Verständnis irrationaler Zahlen erweitern Schülerinnen und Schüler ihr mathematisches Wissen und ihre Fähigkeiten. Irrationale Zahlen ermöglichen es uns, bestimmte mathematische Probleme präzise zu lösen, wie beispielsweise das Berechnen von Flächeninhalten oder das Lösen von Gleichungen.
Wie können Schülerinnen und Schüler irrationale Zahlen kennenlernen?
Die adaptiven Übungen von bettermarks bieten Schülerinnen und Schülern die Möglichkeit, sich mit irrationalen Zahlen vertraut zu machen. Auf dem Tablet, dem Computer oder dem Smartphone können sie interaktive Aufgaben lösen und erhalten personalisierte Rückmeldungen. Die Nutzung von bettermarks hat sich in verschiedenen Ländern als effektives Instrument zur Verbesserung des mathematischen Verständnisses erwiesen. In Uruguay wurde beispielsweise eine dreijährige Studie durchgeführt, bei der ein Lernzuwachs von bis zu 30% festgestellt wurde. In Deutschland nutzen bereits über 400.000 Schülerinnen und Schüler bettermarks im Schuljahr 20/21, wobei mehr als 144 Millionen Aufgaben gelöst wurden.
Der Einsatz von bettermarks zur Vermittlung irrationaler Zahlen
1. Einführung irrationaler Zahlen
Bettermarks bietet Schülerinnen und Schülern die Möglichkeit, sich mit irrationalen Zahlen vertraut zu machen. In den adaptiven Übungen werden verschiedene Aufgaben gestellt, bei denen die Schülerinnen und Schüler lernen, wie irrationalen Zahlen definiert sind und wie sie in der Mathematik verwendet werden. Durch das interaktive Lernen auf dem Tablet, dem Computer oder dem Smartphone können die Schülerinnen und Schüler ihr Wissen über irrationale Zahlen kontinuierlich verbessern.
– Die adaptiven Übungen ermöglichen es den Schülerinnen und Schülern, ihr Verständnis für irrationale Zahlen schrittweise aufzubauen.
– Sie lernen, dass irrationale Zahlen nicht als Bruch dargestellt werden können und dass sie unendlich viele Dezimalstellen haben.
– Durch personalisierte Rückmeldungen erhalten die Schülerinnen und Schüler direkte Unterstützung bei ihren Lernfortschritten.
2. Studie der Regierung von Uruguay
Die Regierung von Uruguay hat eine dreijährige Studie durchgeführt, um die Nutzung von bettermarks im Unterricht zu untersuchen. Dabei wurden auch die Fortschritte der Schülerinnen und Schüler im Bereich irrationaler Zahlen gemessen. Das Ergebnis zeigte einen Lernzuwachs von bis zu 30%. Diese positiven Ergebnisse bestätigen den Einsatz von bettermarks zur Vermittlung komplexer mathematischer Konzepte wie irrationaler Zahlen.
– Die Studie basierte auf UNESCO-Daten und belegt den pädagogischen Mehrwert von bettermarks.
– Durch den Einsatz von bettermarks konnten die Schülerinnen und Schüler ihre Kenntnisse über irrationale Zahlen deutlich verbessern.
– Die personalisierten Rückmeldungen von bettermarks haben den Lernprozess unterstützt und zu einem effektiven Unterricht beigetragen.
Insgesamt hat sich gezeigt, dass der Einsatz von bettermarks im Mathematikunterricht dazu beiträgt, Schülerinnen und Schülern ein besseres Verständnis für irrationale Zahlen zu vermitteln. Die adaptiven Übungen und personalisierten Rückmeldungen ermöglichen es den Schülerinnen und Schülern, ihr Wissen kontinuierlich zu erweitern und ihre mathematischen Fähigkeiten zu verbessern. Die positive Studie der Regierung von Uruguay bestätigt die Wirksamkeit von bettermarks bei der Vermittlung komplexer mathematischer Konzepte.
Studie belegt Lernzuwachs durch bettermarks bei irrationalen Zahlen
Eine dreijährige Studie in Uruguay
Eine dreijährige Studie, die von der Regierung von Uruguay auf Basis von UNESCO-Daten durchgeführt wurde, hat den Lernzuwachs durch die Verwendung von bettermarks bei irrationalen Zahlen belegt. Die adaptiven Übungen von bettermarks ermöglichen es Schülerinnen und Schülern, auf verschiedenen Geräten wie Tablets, Computern und Smartphones zu rechnen und personalisierte Rückmeldungen zu erhalten. Insgesamt konnten bis zu 30% Lernzuwachs festgestellt werden.
Mehr als 144 Millionen Aufgaben gelöst
Im Schuljahr 20/21 haben über 400.000 Schülerinnen und Schüler in Deutschland bettermarks genutzt, um ihre Fähigkeiten im Umgang mit irrationalen Zahlen zu verbessern. Dabei wurden mehr als 144 Millionen Aufgaben gelöst. Die Ergebnisse zeigen, dass die Verwendung von bettermarks einen signifikanten Einfluss auf den Lernerfolg hat.
Internationale Anwendung von bettermarks
Bettermarks ist nicht nur in Deutschland weit verbreitet, sondern wird auch in anderen Ländern wie den Niederlanden, Uruguay und Südafrika täglich im Unterricht eingesetzt. Die Verfügbarkeit des Programms in vier Sprachen ermöglicht es Schülerinnen und Schülern weltweit, ihre mathematischen Fähigkeiten im Bereich irrationaler Zahlen zu verbessern. Die Ergebnisse der Studie bestätigen die Wirksamkeit dieser Methode und zeigen das Potenzial für einen nachhaltigen Lernzuwachs.
Zusammenfassend kann man sagen, dass eine irrationale Zahl eine Dezimalzahl ist, die nicht als Bruch zweier ganzer Zahlen darstellbar ist. Diese Zahlen haben unendlich viele Stellen nach dem Komma und können nicht exakt dargestellt werden. Beispiele für irrationale Zahlen sind π (Pi) und √2 (Wurzel aus 2). Sie spielen eine wichtige Rolle in der Mathematik und haben interessante Eigenschaften.