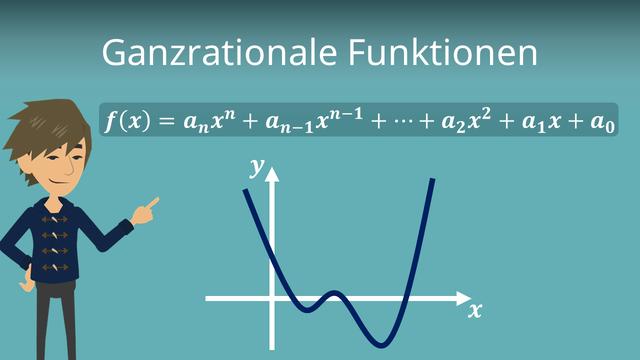
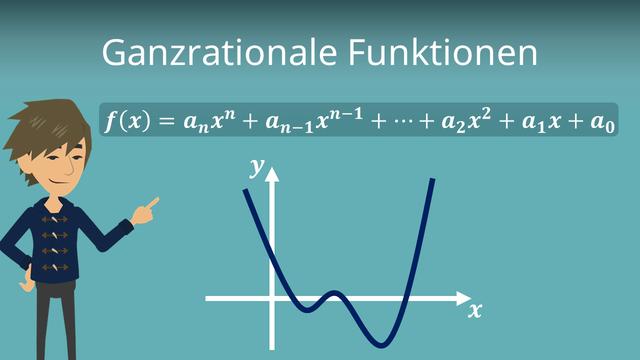
Eine ganzrationale Funktion ist eine mathematische Funktion, die aus Polynomen besteht. Sie wird oft verwendet, um komplexe Zusammenhänge zu beschreiben und zu modellieren. In diesem Artikel werden wir uns näher mit den Eigenschaften und Anwendungen von ganzrationalen Funktionen befassen.
Definition und Eigenschaften von ganzrationalen Funktionen
Ganzrationale Funktionen, auch Polynomfunktionen genannt, sind Funktionen, die aus der Summe einzelner polynomieller Bestandteile in einer Variablen bestehen. Im Gegensatz zu gebrochen rationalen Funktionen enthalten sie keine Brüche.
Eigenschaften von ganzrationalen Funktionen:
- Der höchste Exponent bestimmt den Grad der Funktion. Eine Funktion mit einem höchsten Exponenten von n hat den Grad n.
- Die Koeffizienten vor den Potenzen werden als Koeffizienten bezeichnet.
- Der Faktor vor der höchsten Potenz wird als Leitkoeffizient bezeichnet.
- Ganzrationale Funktionen, die nur aus dem Leitkoeffizienten und einer Potenz bestehen, werden als Potenzfunktionen bezeichnet.
Symmetrie und Grenzwerte:
Ganzrationale Funktion können achsensymmetrisch zur x-Achse oder punktsymmetrisch zum Ursprung sein, abhängig davon, ob sie nur gerade oder ungerade Exponenten enthalten. Wenn eine ganzrationale Funktion sowohl gerade als auch ungerade Exponente enthält, ist sie weder achsensymmetrisch noch punktsymmetrisch.
Die Grenzwerte einer ganzrationaler Funktion hängt vom Grad der Funktion und dem Vorzeichen des Leitkoeffizientes ab. Ganzrationale Funktionen mit geradem Grad ähneln global betrachtet einer quadratischen Funktion, während Funktionen mit ungeradem Grad Ähnlichkeit mit dem Graphen einer kubischen Funktion haben.
Nullstellen und Extrempunkte:
Die Nullstellen einer ganzrationalen Funktion können durch Ausklammern, Anwendung der Mitternachtsformel oder Polynomdivision berechnet werden. Die Anzahl der reellen Nullstellen ist kleiner oder gleich dem Grad der Funktion.
Ganzrationale Funktionen können mehrere Extrempunkte haben, wie Minima, Maxima oder Sattelpunkte. Die Ableitung einer ganzrationalen Funktion vom Grad n ist eine Polynomfunktion vom Grad n-1. Daher kann eine ganzrationale Funktion maximal n-1 Extrempunkte besitzen.
Beispiele für ganzrationale Funktionen:
- Lineare Funktionen: f(x) = ax + b (Grad 1)
- Quadratische Funktionen: f(x) = ax^2 + bx + c (Grad 2)
- Kubische Funktionen: f(x) = ax^3 + bx^2 + cx + d (Grad 3)
- Funktionen höherer Grade: f(x) = ax^n +… (Grad n)
Beispiele und Nichtbeispiele für ganzrationale Funktionen
Beispiele für ganzrationale Funktionen:
– Lineare Funktionen: Eine lineare Funktion ist ein Beispiel für eine ganzrationale Funktion 1. Grades. Sie hat die Form f(x) = ax + b, wobei a und b Konstanten sind.
– Quadratische Funktionen: Eine quadratische Funktion ist ein Beispiel für eine ganzrationale Funktion 2. Grades. Sie hat die Form f(x) = ax^2 + bx + c, wobei a, b und c Konstanten sind.
– Kubische Funktionen: Eine kubische Funktion ist ein Beispiel für eine ganzrationale Funktion 3. Grades. Sie hat die Form f(x) = ax^3 + bx^2 + cx + d, wobei a, b, c und d Konstanten sind.
– Polynomfunktionen höherer Grade: Ganzrationale Funktionen können auch höhere Grade haben, wie zum Beispiel eine ganzrationale Funktion 4. Grades oder eine ganzrationale Funktion 5. Grades.
Nichtbeispiele für ganzrationale Funktionen:
– Gebrochen rationale Funktionen: Gebrochen rationale Funktionen sind keine Beispiele für ganzrationale Funktionen, da sie einen Bruch aus zwei Polynomen als Funktionsausdruck haben.
– Trigonometrische oder exponentielle Funktionen: Trigonometrische oder exponentielle Funktionen sind ebenfalls keine Beispiele für ganzrationale Funktionen, da sie nicht durch Polynome beschrieben werden können.
Es gibt also verschiedene Arten von ganzrationalen Funktionen mit unterschiedlichen Graden und Funktionsformen.
Nullstellen und Grenzwerte von ganzrationalen Funktionen
Nullstellen und Grenzwerte sind wichtige Eigenschaften von ganzrationalen Funktionen. Die Nullstellen einer Funktion sind die Werte, für die die Funktion den Wert null annimmt. Um die Nullstellen zu berechnen, setzt man die Funktion gleich null und löst nach der Variablen auf. Je nach Grad der Funktion gibt es unterschiedliche Methoden, um die Nullstellen zu bestimmen.
Die Grenzwerte einer Funktion geben an, welchen Wert die Funktion für sehr große oder sehr kleine Werte der Variablen annimmt. Sie zeigen das Verhalten der Funktion im Unendlichen. Es gibt verschiedene Möglichkeiten, Grenzwerte zu berechnen, je nachdem ob es sich um eine lineare, quadratische oder höhergradige Funktion handelt.
Ein Beispiel für eine ganzrationale Funktion ist f(x) = 2x^3 – 5x^2 + 3x – 1. Um die Nullstellen dieser Funktion zu berechnen, setzen wir f(x) = 0 und lösen nach x auf:
2x^3 – 5x^2 + 3x – 1 = 0
Das genaue Vorgehen zur Lösung dieser Gleichung hängt vom Grad der Funktion ab. Bei einer kubischen Funktion kann man zum Beispiel das Verfahren von Cardano verwenden.
Die Grenzwerte dieser Funktion können wir bestimmen, indem wir den Ausdruck betrachten, wenn x gegen positive oder negative Unendlichkeit strebt. In diesem Fall würde f(x) gegen positive oder negative Unendlichkeit streben, je nachdem ob der Leitkoeffizient positiv oder negativ ist.
Zusammenfassend kann man sagen, dass Nullstellen und Grenzwerte wichtige Informationen über das Verhalten von ganzrationalen Funktionen liefern. Sie ermöglichen es uns, den Funktionsgraphen zu analysieren und Aussagen über Extrempunkte, Symmetrie und Verhalten im Unendlichen zu machen.
Symmetrie und Verhalten an den Rändern des Definitionsbereichs bei ganzrationalen Funktionen
Bei ganzrationalen Funktionen gibt es verschiedene Eigenschaften, die uns Informationen über ihre Symmetrie und ihr Verhalten an den Rändern des Definitionsbereichs geben können.
Symmetrie
Die Symmetrie einer ganzrationalen Funktion hängt vom Grad der Funktion und den Exponenten ihrer Terme ab. Eine Funktion ist achsensymmetrisch zur x-Achse, wenn sie nur gerade Exponenten enthält. Das bedeutet, dass alle negativen Vorzeichen in der Funktionsgleichung sich gegenseitig aufheben.
Wenn eine ganzrationale Funktion nur ungerade Exponenten enthält, ist sie punktsymmetrisch zum Ursprung. Dies bedeutet, dass für jeden Punkt (x, y) im Funktionsgraph auch der Punkt (-x, -y) auf dem Graph liegt.
Wenn eine Polynomfunktion sowohl gerade als auch ungerade Exponenten enthält, ist sie weder punktsymmetrisch noch achsensymmetrisch.
Verhalten an den Rändern des Definitionsbereichs
Das Verhalten einer ganzrationalen Funktion an den Rändern ihres Definitionsbereichs kann ebenfalls unterschiedlich sein. Es hängt vom Grad der Funktion und dem Vorzeichen des Leitkoeffizienten ab.
Ganzrationale Funktionen mit geradem Grad ähneln global betrachtet einer quadratischen Funktion. Ihre beiden Parabel-Äste laufen in die gleiche Richtung.
Ganzrationale Funktionen mit ungeradem Grad ähneln global betrachtet dem Graphen einer Funktion 3. Grades. Das Vorzeichen des Leitkoeffizienten bestimmt das Verhalten im Unendlichen.
Es ist wichtig, diese Eigenschaften zu beachten, um den Funktionsgraphen einer ganzrationalen Funktion besser verstehen und analysieren zu können.
Unterschiede zwischen Polynomfunktionen und Nicht-Polynomfunktionen
Unterschiede zwischen Polynomfunktionen und Nicht-Polynomfunktionen:
1. Definition: Polynomfunktionen sind Funktionen, die aus der Summe von polynomiellen Bestandteilen in einer Variablen bestehen. Sie haben keine Brüche oder Wurzeln in ihrem Funktionsterm. Nicht-Polynomfunktionen hingegen können Brüche, Wurzeln oder andere nicht-polynomiale Ausdrücke enthalten.
2. Grad: Polynomfunktionen haben einen bestimmten Grad, der durch den höchsten Exponenten im Funktionsterm bestimmt wird. Dieser Grad gibt an, wie die Funktion global betrachtet aussieht und wie sie sich an den Rändern des Definitionsbereichs verhält. Nicht-Polynomfunktionen haben keinen spezifischen Grad.
3. Symmetrie: Polynomfunktionen können achsensymmetrisch zur x-Achse sein, wenn sie nur gerade Exponenten enthalten, oder punktsymmetrisch zum Ursprung sein, wenn sie nur ungerade Exponenten enthalten. Nicht-Polynomfunktionen haben keine solche Symmetriebedingungen.
4. Grenzwerte: Die Grenzwerte von Polynomfunktionen hängen vom Grad der Funktion und vom Vorzeichen des Leitkoeffizienten ab. Ganzrationale Funktionen mit geradem Exponenten ähneln global betrachtet einer quadratischen Funktion, während ganzrationale Funktionen mit ungeradem Grad Ähnlichkeiten mit dem Graph einer kubischen Funktion aufweisen können. Bei Nicht-Polynomfunktionen gibt es keine spezifischen Grenzwertverhalten.
5. Lösungsmöglichkeiten: Für Polynomfunktionen gibt es verschiedene Methoden, um Nullstellen zu berechnen, abhängig vom Grad der Funktion. Bei linearen Funktionen kann man den Term einfach auflösen, bei quadratischen Funktionen helfen die Mitternachtsformel oder die pq-Formel weiter. Für Nicht-Polynomfunktionen gibt es keine solchen allgemeinen Lösungsformeln.
6. Extrempunkte: Polynomfunktionen haben in der Regel mehrere (lokale) Extrempunkte wie Minima, Maxima oder Sattelpunkte. Die Anzahl der Extrempunkte hängt vom Grad der Funktion ab. Nicht-Polynomfunktionen können auch Extrempunkte haben, aber ihre Anzahl und Art sind nicht durch den Grad bestimmt.
Zusammenfassend lassen sich Polynomfunktionen von Nicht-Polynomfunktionen durch ihre Definition, ihren Grad, ihre Symmetrie, ihre Grenzwerte, ihre Lösungsmöglichkeiten und ihre Extrempunkte unterscheiden. Polynomfunktionen sind eine spezielle Art von ganzrationalen Funktionen ohne Brüche oder Wurzeln im Funktionsterm, während Nicht-Polynomfunktionen eine breitere Klasse von Funktionen umfassen können.
Berechnung von Extrempunkten bei ganzrationalen Funktione
Die Berechnung von Extrempunkten bei ganzrationalen Funktionen erfolgt in mehreren Schritten.
Schritt 1: Bestimme die Ableitungsfunktion der gegebenen ganzrationalen Funktion. Die Ableitungsfunktion gibt die Steigung der Funktion an jedem Punkt an.
Schritt 2: Berechne die Nullstellen der Ableitungsfunktion. Diese entsprechen den x-Koordinaten der Extrempunkte der ursprünglichen Funktion.
Schritt 3: Setze die berechneten x-Werte in die ursprüngliche Funktion ein, um die zugehörigen y-Koordinaten der Extrempunkte zu bestimmen.
Schritt 4: Untersuche die Art der Extrempunkte, indem du das Verhalten der Funktion vor und nach dem Extrempunkt betrachtest. Wenn sich das Vorzeichen der Steigung ändert, handelt es sich um einen Sattelpunkt. Wenn die Steigung vor dem Extrempunkt negativ ist und nach dem Extrempunkt positiv wird, handelt es sich um ein lokales Minimum. Wenn die Steigung vor dem Extrempunkt positiv ist und nach dem Extrempunkt negativ wird, handelt es sich um ein lokales Maximum.
Beispiel:
Gegeben sei die ganzrationale Funktion f(x) = x^3 – 6x^2 + 9x + 2.
Schritt 1: Berechne die Ableitungsfunktion f'(x) = 3x^2 -12x +9.
Schritt 2: Berechne die Nullstellen von f'(x) durch Auflösen der Gleichung 3x^2 -12x +9 = 0. In diesem Fall ergibt sich x = 1 als einzige Nullstelle.
Schritt 3: Setze x = 1 in die ursprüngliche Funktion ein, um die y-Koordinate des Extrempunkts zu bestimmen. Es ergibt sich f(1) = 6.
Schritt 4: Untersuche das Verhalten der Funktion vor und nach dem Extrempunkt. Da die Steigung vor dem Extrempunkt negativ ist und nach dem Extrempunkt positiv wird, handelt es sich um ein lokales Minimum bei (1,6).
Dieser Prozess kann für jede ganzrationale Funktion wiederholt werden, um die Extrempunkte zu berechnen.
Eine ganzrationale Funktion ist eine mathematische Funktion, die durch Polynome dargestellt wird. Sie ermöglicht es, komplexe Zusammenhänge und Veränderungen in Form von Kurven darzustellen. Durch ihre vielseitige Anwendung in verschiedenen Bereichen der Mathematik und Naturwissenschaften ist sie ein wichtiges Konzept für das Verständnis von Funktionen und deren Eigenschaften.