Eine Funktionsgleichung ist eine mathematische Gleichung, die den Zusammenhang zwischen zwei Variablen beschreibt. Sie wird verwendet, um die Beziehung und Abhängigkeit zwischen einer unabhängigen Variable (x) und einer abhängigen Variable (y) darzustellen. Diese Gleichungen spielen eine wichtige Rolle in der Mathematik, da sie es ermöglichen, verschiedene Aspekte von Funktionen zu analysieren und zu verstehen. In diesem Artikel werden wir uns genauer mit dem Konzept der Funktionsgleichungen befassen und ihre Bedeutung in der Mathematik erklären.
- Wikinger Kostüm selber machen: Einfache Anleitung für Damen
- Leckere Dinkelbrötchen selber machen – einfaches und vielfältiges Rezept!
- Uiguren in China: Menschenrechtsverletzungen bis ins Schlafzimmer – Report enthüllt Grausamkeiten
- Wetterprognose: Wie wird das Wetter im Februar 2023?
- Einfaches Zuckerguss Grundrezept für leckere Backwerke
Grundlagen einer Funktionsgleichung verstehen
Was ist eine Funktionsgleichung?
Eine Funktionsgleichung beschreibt den Zusammenhang zwischen zwei Variablen in einer mathematischen Funktion. Sie wird oft in Form einer Gleichung dargestellt, bei der eine Variable von der anderen abhängig ist. Eine typische Funktionsgleichung sieht zum Beispiel so aus: y = mx + b. Hierbei steht y für die abhängige Variable, x für die unabhängige Variable und m sowie b für Konstanten. Die Funktionsgleichung gibt an, wie sich der Wert von y verändert, wenn sich der Wert von x ändert.
Wie liest man eine Funktionsgleichung?
Um eine Funktionsgleichung zu lesen und zu verstehen, ist es wichtig, die Symbole und deren Bedeutungen zu kennen. In der oben genannten Beispielgleichung bedeutet m die Steigung der Funktion und b den y-Achsenabschnitt. Die Steigung gibt an, wie stark die Funktion ansteigt oder abfällt, während der y-Achsenabschnitt den Punkt angibt, an dem die Funktion die y-Achse schneidet.
Wie verwendet man eine Funktionsgleichung?
Funktionsgleichungen werden verwendet, um mathematische Beziehungen zwischen Variablen darzustellen und zu analysieren. Mit Hilfe einer Funktionsgleichung kann man beispielsweise den Verlauf eines Graphen zeichnen oder bestimmte Werte berechnen. Durch Manipulation der Gleichung können auch verschiedene Eigenschaften der Funktion abgeleitet werden, wie beispielsweise die Nullstellen oder Extrempunkte.
Zusammenfassend lässt sich sagen, dass eine Funktionsgleichung den Zusammenhang zwischen zwei Variablen in einer mathematischen Funktion beschreibt. Sie ist eine wichtige Methode zur Darstellung und Analyse von mathematischen Beziehungen und wird in vielen Bereichen der Mathematik und Naturwissenschaften verwendet.
Was versteht man unter einer Funktionsgleichung?
Eine Funktionsgleichung ist eine mathematische Gleichung, die den Zusammenhang zwischen zwei Variablen beschreibt. Sie wird verwendet, um eine Funktion darzustellen, bei der jeder Wert der unabhängigen Variable (x) einem bestimmten Wert der abhängigen Variable (y) zugeordnet wird. Eine Funktionsgleichung kann auf verschiedene Arten dargestellt werden, wie zum Beispiel als lineare Gleichung, quadratische Gleichung oder exponentielle Gleichung.
Um eine Funktionsgleichung zu erstellen, müssen wir zunächst die Art der Funktion identifizieren. Zum Beispiel könnte es sich um eine lineare Funktion handeln, bei der die abhängige Variable proportional zur unabhängigen Variable ist. In diesem Fall würde die Funktionsgleichung in der Form y = mx + b geschrieben werden, wobei m die Steigung und b der y-Achsenabschnitt ist.
Eine Funktionsgleichung kann auch als Graph dargestellt werden. Der Graph zeigt den Zusammenhang zwischen den beiden Variablen und ermöglicht es uns, das Verhalten der Funktion visuell zu verstehen. Durch die Analyse des Graphen können wir Informationen über Steigung, Nullstellen und Extremwerte ableiten.
Insgesamt ist eine Funktionsgleichung ein wichtiges Werkzeug in der Mathematik, um den Zusammenhang zwischen Variablen zu beschreiben und mathematische Modelle für reale Situationen zu entwickeln. Sie ermöglicht es uns, Vorhersagen zu machen und Probleme in verschiedenen Bereichen wie Physik, Wirtschaft und Ingenieurwesen zu lösen.
Die Bedeutung einer Funktionsgleichung erklärt
Eine Funktionsgleichung ist eine mathematische Darstellung, die den Zusammenhang zwischen zwei Variablen beschreibt. Sie wird verwendet, um die Beziehung zwischen einer unabhängigen Variable (x) und einer abhängigen Variable (y) zu definieren. Eine Funktionsgleichung ermöglicht es uns, Werte für die abhängige Variable basierend auf verschiedenen Werten der unabhängigen Variable zu berechnen.
Die Komponenten einer Funktionsgleichung:
– Unabhängige Variable: Die unabhängige Variable (x) ist die Eingabe oder der Wert, der in die Funktion eingesetzt wird.
– Abhängige Variable: Die abhängige Variable (y) ist das Ergebnis oder der Wert, der durch die Funktion berechnet wird.
– Funktionsvorschrift: Die Funktionsvorschrift gibt an, wie die unabhängige und abhängige Variable miteinander verknüpft sind. Sie besteht aus mathematischen Operationen wie Addition, Subtraktion, Multiplikation und Division sowie Potenzierung oder Wurzelziehen.
Beispiel einer Funktionsgleichung:
Eine einfache Funktionsgleichung könnte wie folgt aussehen: y = 2x + 3. In dieser Gleichung ist x die unabhängige Variable und y die abhängige Variable. Die Funktion gibt an, dass der Wert von y das Doppelte des Wertes von x plus 3 ist.
Durch das Einsetzen verschiedener Werte für x können wir nun den entsprechenden Wert für y berechnen. Zum Beispiel, wenn x = 2 ist, ergibt sich y = 2(2) + 3 = 7. Somit haben wir den Wert der abhängigen Variable basierend auf dem gegebenen Wert der unabhängigen Variable ermittelt.
Funktionsgleichungen sind ein wichtiges Werkzeug in der Mathematik und werden in vielen Bereichen wie Physik, Wirtschaft und Ingenieurwesen verwendet. Sie ermöglichen es uns, komplexe Beziehungen zwischen Variablen zu modellieren und Vorhersagen über das Verhalten von Systemen zu treffen.
Wie funktioniert eine Funktionsgleichung?
Eine Funktionsgleichung beschreibt den Zusammenhang zwischen einer unabhängigen Variablen und einer abhängigen Variablen in Form einer mathematischen Gleichung. Sie ermöglicht es uns, den Verlauf einer Funktion grafisch darzustellen und Berechnungen durchzuführen. Eine Funktionsgleichung besteht aus verschiedenen Elementen wie Variablen, Konstanten und mathematischen Operationen.
Aufbau einer Funktionsgleichung:
Um eine Funktionsgleichung aufzustellen, müssen wir zunächst die unabhängige Variable definieren. Dies ist die Variable, von der der Wert abhängig ist. Wir verwenden oft den Buchstaben „x“ für die unabhängige Variable. Die abhängige Variable wird dann in Abhängigkeit von „x“ angegeben und kann mit einem anderen Buchstaben wie „y“ oder „f(x)“ bezeichnet werden.
Die Funktionsgleichung selbst besteht aus mathematischen Ausdrücken wie Addition (+), Subtraktion (-), Multiplikation (*), Division (/) und Potenzierung (^). Diese Operationen werden verwendet, um den Zusammenhang zwischen der unabhängigen und abhängigen Variable zu beschreiben. Zusätzlich können Konstanten in die Gleichung eingefügt werden, um spezifische Werte oder Verschiebungen anzugeben.
Grafische Darstellung einer Funktionsgleichung:
Eine Funktionsgleichung ermöglicht es uns auch, den Verlauf der Funktion grafisch darzustellen. Dies geschieht durch das Einsetzen verschiedener Werte für die unabhängige Variable „x“ und das Berechnen der entsprechenden Werte für die abhängige Variable. Die resultierenden Wertepaare können dann in ein Koordinatensystem eingetragen werden, um die Funktion grafisch darzustellen.
Durch die grafische Darstellung einer Funktionsgleichung können wir den Verlauf der Funktion analysieren, Extremstellen bestimmen, Schnittpunkte mit den Achsen finden und weitere Eigenschaften der Funktion untersuchen. Dies ermöglicht es uns, mathematische Modelle zu erstellen und reale Phänomene zu beschreiben oder Vorhersagen zu treffen.
Die Struktur einer Funktionsgleichung verstehen
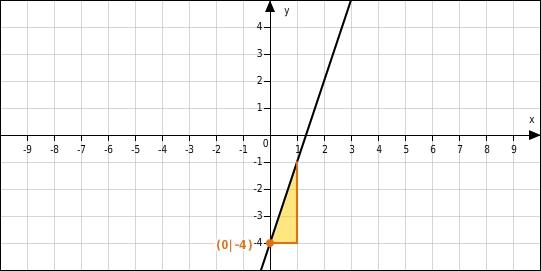
1. Die Grundstruktur einer Funktionsgleichung
Eine Funktionsgleichung besteht aus verschiedenen Elementen, die alle eine bestimmte Bedeutung haben. Die grundlegende Struktur einer Funktionsgleichung ist wie folgt: f(x) = mx + b. Dabei steht f(x) für die abhängige Variable, also den Funktionswert, m für die Steigung der Funktion und b für den y-Achsenabschnitt. Diese drei Elemente sind essenziell, um eine Funktion eindeutig zu beschreiben.
2. Die Bedeutung der Steigung (m)
Die Steigung (m) in einer Funktionsgleichung gibt an, wie stark die Funktion ansteigt oder abfällt. Eine positive Steigung bedeutet einen Anstieg der Funktion von links nach rechts, während eine negative Steigung einen Abfall der Funktion darstellt. Je größer der Betrag der Steigung ist, desto steiler verläuft die Funktion.
3. Der y-Achsenabschnitt (b)
Der y-Achsenabschnitt (b) gibt den Wert an, den die Funktion annimmt, wenn x = 0 ist. Er repräsentiert den Schnittpunkt der Funktion mit der y-Achse. Wenn b positiv ist, liegt dieser Punkt oberhalb der x-Achse, bei negativem b liegt er unterhalb.
Zusammenfassend lässt sich sagen, dass eine Funktionsgleichung aus den Elementen f(x), m und b besteht und diese gemeinsam die Struktur und Eigenschaften einer Funktion beschreiben. Die Steigung (m) gibt an, wie stark die Funktion ansteigt oder abfällt, während der y-Achsenabschnitt (b) den Schnittpunkt mit der y-Achse angibt. Durch das Verständnis dieser Struktur können wir Funktionen analysieren und deren Verhalten besser verstehen.
Anwendungen und Beispiele von Funktionsgleichungen
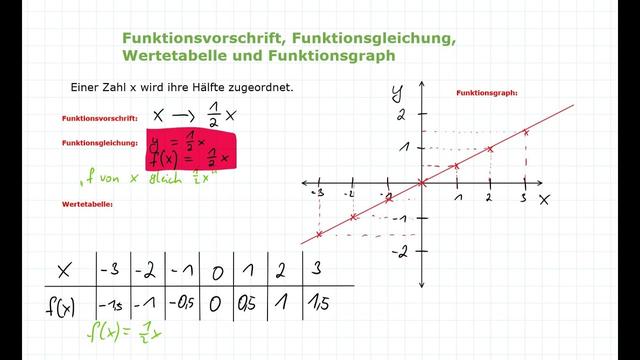
1. Anwendung in der Physik
Eine der wichtigsten Anwendungen von Funktionsgleichungen findet sich in der Physik. Hier werden Funktionsgleichungen verwendet, um die Bewegung von Objekten zu beschreiben. Zum Beispiel kann die Funktion y = f(x) verwendet werden, um den Weg eines Körpers in Abhängigkeit von der Zeit zu beschreiben. Die Gleichung kann dann genutzt werden, um verschiedene Aspekte wie Geschwindigkeit, Beschleunigung oder Position des Körpers zu berechnen.
Beispielhaft könnte eine Funktion wie y = -4.9x^2 + 10x + 5 verwendet werden, um die Flugbahn eines geworfenen Balls zu beschreiben. Hierbei steht y für die Höhe des Balls über dem Boden und x für die vergangene Zeit seit dem Wurf. Durch das Lösen dieser Funktionsgleichung können wir den Zeitpunkt berechnen, an dem der Ball seine maximale Höhe erreicht oder den Punkt, an dem er wieder auf dem Boden landet.
2. Anwendung in der Wirtschaft
Funktionsgleichungen finden auch in der Wirtschaft Anwendung, insbesondere bei der Analyse von Kosten- und Erlösmodellen. Eine Funktion kann verwendet werden, um den Zusammenhang zwischen Produktionsmenge und Kosten oder Gewinn darzustellen.
Ein Beispiel dafür ist die Kostenfunktion C(x) = 1000 + 5x, wobei x für die produzierte Menge eines Produkts steht und C(x) für die damit verbundenen Kosten. Diese Funktion kann verwendet werden, um die Gesamtkosten für eine bestimmte Produktionsmenge zu berechnen. Ebenso kann die Erlösfunktion R(x) = 10x verwendet werden, um den Umsatz in Abhängigkeit von der produzierten Menge zu berechnen.
Durch das Lösen dieser Funktionsgleichungen können Unternehmen wichtige Entscheidungen treffen, wie z.B. die optimale Produktionsmenge zur Maximierung des Gewinns oder den Break-Even-Punkt, an dem die Kosten und Erlöse gleich sind.
Diese Anwendungen zeigen, wie Funktionsgleichungen in verschiedenen Bereichen eingesetzt werden können, um komplexe Zusammenhänge zu modellieren und zu analysieren. Sie ermöglichen es uns, mathematische Modelle zu entwickeln und daraus nützliche Informationen abzuleiten.
Zusammenfassend ist eine Funktionsgleichung eine mathematische Darstellung, die den Zusammenhang zwischen Variablen in einer Funktion beschreibt. Sie ermöglicht es uns, die Beziehung zwischen Eingabe- und Ausgabewerten zu verstehen und zu analysieren. Durch das Lösen einer Funktionsgleichung können wir auch unbekannte Werte berechnen und Vorhersagen über das Verhalten der Funktion machen. Insgesamt ist die Funktionsgleichung ein wichtiges Werkzeug in der Mathematik, um komplexe Zusammenhänge zu modellieren und Probleme zu lösen.