Alles Wissenswerte über die Determinante einer Matrix

Eine Determinante ist ein mathematisches Konzept, das in der linearen Algebra verwendet wird. Sie gibt Informationen über bestimmte Eigenschaften einer quadratischen Matrix und kann unter anderem zur Lösung von Gleichungssystemen oder zur Berechnung von Volumen verwendet werden. In diesem Artikel werden wir näher auf die Definition, Eigenschaften und Anwendungen der Determinante eingehen.

Die Determinante einer Matrix: Was ist das?

Die Definition der Determinante

Die Determinante einer Matrix ist eine bestimmte Zahl, die der Matrix zugeordnet wird. Sie wird mit det(A) oder |A| gekennzeichnet. Die Determinante kann nur für quadratische Matrizen bestimmt werden. Zum Beispiel wird der Einheitsmatrix E die Zahl 1 zugeordnet.

Eigenschaften der Determinante

Die Determinante einer Matrix gibt uns interessante Informationen über die Matrix. Sie sagt uns zum Beispiel, ob eine Matrix invertierbar ist oder nicht. Ist die Determinante gleich Null, ist die Matrix nicht invertierbar. Umgekehrt gilt auch: Wenn eine Matrix nicht invertierbar ist, dann ist ihre Determinante Null.

Zudem gibt es einige Eigenschaften der Determinante, die es uns ermöglichen, sie zu berechnen und zu manipulieren:
– Wenn wir die Zeilen und Spalten einer Matrix vertauschen und dadurch eine transponierte Matrix AT bilden, ändert sich die Determinante nicht.
– Multiplizieren wir eine Zeile oder Spalte mit einem Skalar λ (einer Zahl), so ist die Determinante der neuen Matrix genau das λ-fache der ursprünglichen Determinante.
– Für das Produkt zweier Matrizen A und B gilt: Die Determinante von A mal B ergibt sich aus dem Produkt der einzelnen Determinanten von A und B.

Für kleinere Matrizen wie 2×2 oder 3×3 gibt es spezielle Regeln zur Berechnung der Determinanten. Für größere Matrizen empfiehlt es sich, ein entsprechendes Video anzuschauen.

Zusammenfassung

Die Determinante einer Matrix ist eine Zahl, die der Matrix zugeordnet wird und uns Informationen über die Matrix liefert. Sie gibt Auskunft darüber, ob eine Matrix invertierbar ist oder nicht. Durch bestimmte Eigenschaften der Determinante können wir sie berechnen und manipulieren. Für kleinere Matrizen gibt es spezielle Regeln zur Berechnung, während für größere Matrizen Videos empfohlen werden.

Eigenschaften und Bedeutung der Determinante einer Matrix

Die Determinante einer Matrix A ist eine bestimmte Zahl, die der Matrix zugeordnet wird. Sie wird mit det(A) oder |A| gekennzeichnet. Die Determinante kann nur für quadratische Matrizen bestimmt werden.

Eine wichtige Eigenschaft der Determinante ist, dass sie dir Informationen über die Invertierbarkeit einer Matrix liefert. Ist die Determinante gleich Null, bedeutet dies, dass die Matrix nicht invertierbar ist. Andersherum gilt auch: Ist eine Matrix nicht invertierbar, so ist ihre Determinante gleich Null.

Die Berechnung der Determinante erfolgt oft mithilfe des Laplaceschen Entwicklungssatzes. Dieser ermöglicht es, die Determinante einer Matrix durch das Entwickeln nach den Zeilen oder Spalten zu berechnen.

Weitere Eigenschaften der Determinante sind:
– Wenn du die Zeilen und Spalten deiner Matrix vertauschst, um die transponierte Matrix AT zu bilden, ändert sich die Determinante nicht.
– Multiplizierst du eine Zeile oder Spalte mit einer Zahl λ (auch Skalar genannt), so ist die Determinante deiner neuen Matrix das λ-fache der ursprünglichen Determinante.
– Die Determinante der Inversen einer invertierbaren Matrix A ist genau det(A)-1.
– Die Determinante eines Produkts aus Matrizen A und B erhält man durch Multiplikation der einzelnen Determinanten von A und B.

Wenn du die Berechnung der Determinante für spezifische Matrizengrößen lernen möchtest, gibt es verschiedene Regeln. Für 2×2 Matrizen gibt es eine einfache Regel zur Berechnung der Determinante, und für 3×3 Matrizen gibt es die Regel von Sarrus. Bei größeren Matrizen empfiehlt sich die Nutzung von speziellen Verfahren, die in einem entsprechenden Video erklärt werden.

Insgesamt liefert die Determinante einer Matrix wichtige Informationen über ihre Eigenschaften und Invertierbarkeit.

Berechnung der Determinante: Der Laplacesche Entwicklungssatz

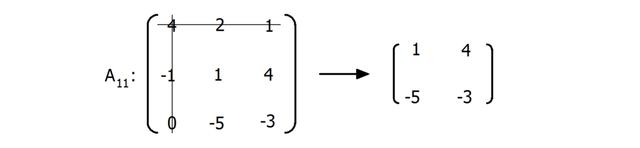
Der Laplacesche Entwicklungssatz ist eine Methode zur Berechnung der Determinante einer Matrix. Dabei wird die Determinante in kleinere Teile aufgeteilt, indem man eine Zeile oder Spalte auswählt und diese mit den Kofaktoren multipliziert.

1. Wähle eine beliebige Zeile oder Spalte aus der Matrix A.

2. Multipliziere jeden Eintrag dieser Zeile bzw. Spalte mit dem Kofaktor, der sich ergibt, wenn man den Eintrag streicht und die verbleibende Untermatrix bildet.

3. Addiere alle diese Produkte zusammen, um die Determinante zu erhalten.

Beispiel:
Gegeben sei folgende 3×3 Matrix A:

A = | a11 a12 a13 |
| a21 a22 a23 |
| a31 a32 a33 |

Wir wählen beispielsweise die erste Zeile aus und berechnen die Determinante mit dem Laplaceschen Entwicklungssatz:

det(A) = a11 * det(A11) – a12 * det(A12) + a13 * det(A13)

Hierbei sind A11, A12 und A13 die Untermatrizen, die entstehen, wenn man jeweils einen Eintrag der ersten Zeile streicht.

Die Berechnung der Untermatrizen erfolgt nach demselben Prinzip wie bei der Ausgangsmatrix: Man wählt eine Zeile oder Spalte aus und wiederholt den Prozess.

Dieser Schritt wird solange wiederholt, bis man auf eine 2×2 Matrix stößt. Für diese kann man die Determinante direkt berechnen, indem man das Produkt der Diagonalelemente bildet und diese subtrahiert.

Die Berechnung der Determinante mit dem Laplaceschen Entwicklungssatz kann bei größeren Matrizen zeitaufwändig sein. Es gibt jedoch effizientere Verfahren wie die LU-Zerlegung oder das Gaußsche Eliminationsverfahren, um die Determinante zu bestimmen.

Es ist wichtig zu beachten, dass der Laplacesche Entwicklungssatz nur für quadratische Matrizen gilt. Für nicht-quadratische Matrizen existiert keine Determinante.

Determinanten von Transportierten Matrizen bleiben unverändert

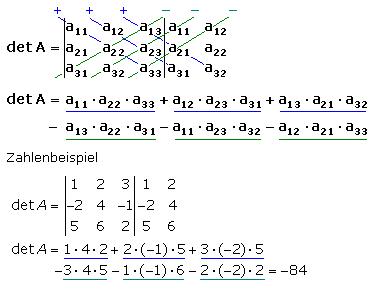
Die Determinante einer Matrix ändert sich nicht, wenn die Zeilen und Spalten vertauscht werden

Eine interessante Eigenschaft der Determinante einer Matrix ist, dass sie unverändert bleibt, wenn man die Zeilen und Spalten der Matrix vertauscht, um die sogenannte „Transportierte“ zu bilden. Das bedeutet, dass die Determinante der Transportierten Matrix genau gleich der Determinante der ursprünglichen Matrix ist.

Diese Eigenschaft kann nützlich sein, um bestimmte Informationen über eine Matrix zu erhalten. Wenn man beispielsweise die Determinante einer Matrix berechnen möchte, aber feststellt, dass es einfacher ist, die Zeilen und Spalten zu vertauschen, kann man dies tun und trotzdem das gleiche Ergebnis erhalten.

Es ist wichtig anzumerken, dass diese Eigenschaft nur für quadratische Matrizen gilt. Eine nicht-quadratische Matrix hat keine Determinante.

Zusammenfassend lässt sich sagen, dass die Determinante einer Transportierten Matrix unverändert bleibt und somit eine nützliche Eigenschaft ist, um Informationen über eine Matrix zu erhalten.

Multiplikation einer Zeile/Spalte mit einem Skalar: Auswirkungen auf die Determinante

Wenn du eine Zeile oder eine Spalte deiner Matrix mit einem Skalar (einer Zahl) multiplizierst, hat dies bestimmte Auswirkungen auf die Determinante der Matrix. Hier sind einige wichtige Punkte zu beachten:

1. Multiplikation einer Zeile/Spalte mit einem positiven Skalar:
– Die Determinante der neuen Matrix ist das Produkt des Skalars und der ursprünglichen Determinante.
– Zum Beispiel, wenn du die erste Zeile deiner Matrix A mit 2 multiplizierst, dann ist die Determinante der neuen Matrix 2 * det(A).

2. Multiplikation einer Zeile/Spalte mit einem negativen Skalar:
– Die Determinante der neuen Matrix ist das negative Produkt des Skalars und der ursprünglichen Determinante.
– Wenn du zum Beispiel die zweite Spalte deiner Matrix B mit -3 multiplizierst, dann ist die Determinante der neuen Matrix -3 * det(B).

3. Multiplikation einer Zeile/Spalte mit dem Wert Null:
– Wenn du eine Zeile oder eine Spalte deiner Matrix mit Null multiplizierst, wird die gesamte Determinante gleich Null.
– Das bedeutet, dass deine neue Matrix nicht invertierbar ist.

Es ist wichtig zu beachten, dass diese Regeln nur gelten, wenn deine Matrix quadratisch ist. Für rechteckige Matrizen gibt es andere Methoden zur Berechnung der Determinante.

Um ein besseres Verständnis für diese Konzepte zu bekommen, empfehlen wir dir unser Video anzuschauen, in dem wir die Auswirkungen der Multiplikation einer Zeile/Spalte mit einem Skalar auf die Determinante einer Matrix genauer erklären.

Berechnung der Determinante für verschiedene Matrixgrößen

Die Berechnung der Determinante einer Matrix hängt von ihrer Größe ab. Hier sind einige Methoden, um die Determinante für verschiedene Matrixgrößen zu berechnen:

1. 2×2-Matrix

Für eine 2×2-Matrix A = [[a, b], [c, d]] lautet die Formel zur Berechnung der Determinante:

• det(A) = ad – bc

2. 3×3-Matrix (Regel von Sarrus)

Für eine 3×3-Matrix A = [[a, b, c], [d, e, f], [g, h, i]] lautet die Formel zur Berechnung der Determinante:

• det(A) = aei + bfg + cdh – ceg – afh – bdi

3. Größere Matrizen (Entwicklungssatz nach Laplace)

Für Matrizen größer als 3×3 kann der Entwicklungssatz nach Laplace verwendet werden. Dabei wird die Determinante durch Entwicklung entlang einer Zeile oder Spalte in kleinere Untermatrizen aufgeteilt und rekursiv berechnet.

Zum Beispiel kann die Determinante einer 4×4-Matrix A wie folgt berechnet werden:

• wähle eine Zeile oder Spalte aus (z.B. die erste Zeile)
• bilde für jeden Eintrag dieser Zeile oder Spalte eine Untermatrix durch Streichen der entsprechenden Zeile und Spalte
• berechne die Determinante jeder Untermatrix (rekursiv)
• multipliziere jede Determinante mit dem entsprechenden Eintrag aus der gewählten Zeile oder Spalte
• addiere oder subtrahiere die Produkte, abhängig von ihrer Position in der Zeile oder Spalte

Diese Methode kann auf Matrizen beliebiger Größe angewendet werden, erfordert jedoch viel Rechenleistung.

In der Mathematik ist eine Determinante eine Zahl, die einer quadratischen Matrix zugeordnet wird. Sie gibt Aufschluss über wichtige Eigenschaften der Matrix und ermöglicht es, lineare Gleichungssysteme zu lösen sowie das Verhalten von Vektoren und linearen Abbildungen zu analysieren. Die Determinante ist ein essentielles Konzept in der linearen Algebra und findet Anwendung in verschiedenen mathematischen Disziplinen sowie in der Physik und Ingenieurwissenschaften.