Was ist ein Scheitelpunkt und wie finde ich ihn?

Ein Scheitelpunkt ist ein Begriff aus der Mathematik und beschreibt den höchsten oder tiefsten Punkt einer Kurve. In diesem Zusammenhang kann der Scheitelpunkt einer Parabel oder eines Graphen als Wendepunkt betrachtet werden. Er gibt Auskunft über den Verlauf und die Steigung einer Funktion. Der Scheitelpunkt ist von besonderer Bedeutung, da er wichtige Informationen über das Verhalten der Kurve liefert und bei verschiedenen mathematischen Berechnungen eine Rolle spielt.

Was ist ein Scheitelpunkt und wie kann er bestimmt werden?

Ein Scheitelpunkt ist der tiefste oder höchste Punkt einer Parabel. Er kann auf verschiedene Weisen bestimmt werden.

1. Ablesen des Scheitelpunkts: Bei einem Graphen kann der Scheitelpunkt abgelesen werden. Der tiefste Punkt einer Parabel wird als Scheitelpunkt bezeichnet, während der höchste Punkt ebenfalls ein Scheitelpunkt ist. Durch das Ablesen der Koordinaten des Scheitelpunkts kann er bestimmt werden.

2. Verwendung der Scheitelpunktform: Wenn die Funktion bereits in der Scheitelpunktform gegeben ist, kann der Scheitel einfach abgelesen werden. Dabei müssen die Vorzeichen der Zahlen beachtet werden. Zum Beispiel wird aus (x + 1) in der allgemeinen Form (x – (-1)), um den Wert von d zu bestimmen. Durch diese Methode kann der Scheitel einer quadratischen Funktion leicht gefunden werden.

3. Umformung durch quadratische Ergänzung oder andere Methoden: Falls die Funktion nicht in der Scheitelpunktform gegeben ist, kann sie durch quadratische Ergänzung oder andere Methoden wie Ausmultiplizieren, Ausklammern oder binomische Formeln umgeformt werden, um den Scheitel zu bestimmen.

4. Bestimmung durch Ableitung: Eine fortgeschrittene Methode zur Bestimmung des Scheitels besteht darin, die Ableitungsfunktion zu verwenden. Da die Steigung am Scheitel einer Funktion immer 0 ist, können die Nullstellen der Ableitung berechnet werden, um den Scheitel zu finden.

5. Bestimmung durch Nullstellen und Achsensymmetrie: Wenn eine Parabel Nullstellen hat, liegt die x-Koordinate des Scheitels genau in der Mitte der beiden Nullstellen. Dies liegt daran, dass alle Parabeln achsensymmetrisch sind. Wenn die Parabel nur eine Nullstelle hat, liegt diese auf der x-Achse und ist gleichzeitig der Scheitel der Funktion.

Durch diese verschiedenen Methoden kann der Scheitelpunkt einer quadratischen Funktion bestimmt werden.

Bestimmung des Scheitelpunkts: Methoden und Beispiele

Der Scheitelpunkt einer Parabel ist der tiefste oder höchste Punkt auf dem Graphen. Es gibt verschiedene Methoden, um den Scheitelpunkt einer quadratischen Funktion zu bestimmen.

Methode 1: Ablesen des Scheitelpunkts aus der Scheitelpunktform

Wenn die Funktion bereits in der Scheitelpunktform vorliegt, kann der Scheitelpunkt direkt abgelesen werden. Die Form ist f(x) = a · (x – d)^2 + e, wobei der Scheitel im Punkt S(d|e) liegt.

Methode 2: Umformen der Funktion durch quadratische Ergänzung oder Ausmultiplizieren/Ausklammern/binomische Formeln

Falls die Funktion nicht in der Scheitelpunktform gegeben ist, kann sie durch quadratische Ergänzung oder andere Umformungen umgeformt werden. Anschließend kann Methode 1 angewendet werden, um den Scheitelpunkt zu bestimmen.

Methode 3: Bestimmung des Scheitelpunkts durch Ableitung

Eine fortgeschrittene Methode zur Bestimmung des Scheitelpunkts ist die Ableitung der Funktion. Da die Steigung am Scheitel immer 0 ist, können die Nullstellen der Ableitung verwendet werden, um den Scheitelpunkt zu berechnen. Dazu geht man folgendermaßen vor:

1. Leite die Funktion f(x) ab.
2. Bestimme die Nullstellen der Ableitung f'(x), da sie die Extremstellen der Funktion sind.
3. Setze die x-Koordinate des Scheitelpunkts in die ursprüngliche Funktion f(x) ein, um die y-Koordinate zu berechnen.

Mit diesen Methoden kannst du den Scheitelpunkt von quadratischen Funktionen bestimmen und somit wichtige Informationen über den Verlauf der Parabel erhalten.

Scheitelpunkt von quadratischen Funktionen: verschiedene Ansätze

Ein Scheitelpunkt ist der tiefste oder höchste Punkt einer Parabel. Es gibt verschiedene Ansätze, um den Scheitelpunkt einer quadratischen Funktion zu bestimmen:

1. Scheitelpunktform

Wenn die Funktion bereits in der Scheitelpunktform gegeben ist, kann der Scheitel direkt abgelesen werden. Dabei muss jedoch auf die Vorzeichen geachtet werden. Zum Beispiel: Die Funktion f(x) = (x + 1)^2 + 7 hat den Scheitelpunkt S(-1|7).

2. Quadratische Ergänzung

Falls die Funktion nicht in der Scheitelpunktform vorliegt, kann sie durch quadratische Ergänzung umgeformt werden. Dadurch wird der Scheitelpunkt sichtbar gemacht. Zum Beispiel: Durch quadratische Ergänzung ergibt sich aus der Funktion f(x) = x^2 + 4x + 5 der Scheitelpunkt S(-2|-1).

3. Ableitung

Eine weitere Methode zur Bestimmung des Scheitelpunkts ist die Ableitung der Funktion. Da die Steigung am Scheitel immer null ist, können die Nullstellen der Ableitung berechnet werden, um den Scheitelpunkt zu finden. Zum Beispiel: Durch Ableiten und Nullsetzen erhält man bei f(x) = x^2 – 4x + 3 den Scheitelpunkt S(2| -1).

Es ist auch möglich, den Scheitelpunkt mithilfe von Ausmultiplizieren, Ausklammern oder den binomischen Formeln zu bestimmen.

Zusätzlich kann bei Parabeln mit Nullstellen die x-Koordinate des Scheitels als der Mittelpunkt zwischen den beiden Nullstellen gefunden werden, da Parabeln achsensymmetrisch sind. Die y-Koordinate des Scheitels ergibt sich dann durch Einsetzen der x-Koordinate in die Funktion.

Die quadratische Ergänzung ist eine hilfreiche Methode, um auch bei komplexeren Funktionen den Scheitelpunkt zu finden.

Bestimmung des Scheitelpunkts durch Ableitung

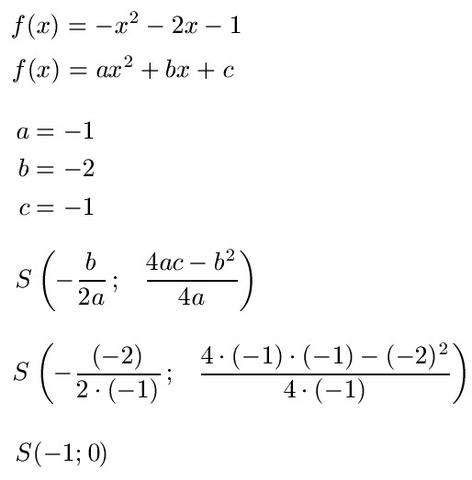
Um den Scheitelpunkt einer Funktion mithilfe der Ableitung zu bestimmen, kannst du folgende Schritte befolgen:

1. Leite die Funktion f(x) ab. Die Ableitung beschreibt die Steigung der Funktion.

2. Bestimme die Nullstellen der Ableitung f'(x). Diese stellen die Extrempunkte (Maxima und Minima) der Funktion dar und entsprechen den Scheitelpunkten.

3. Setze die x-Koordinate der Nullstellen in die ursprüngliche Funktion f(x) ein, um die y-Koordinate des Scheitelpunkts zu berechnen.

Ein Beispiel zur Verdeutlichung:
Gegeben ist die Funktion f(x) = 2x^2 – 5x + 3.

1. Ableiten der Funktion:
f'(x) = 4x – 5

2. Bestimmung der Nullstelle:
4x – 5 = 0
4x = 5
x = 5/4

Die Nullstelle beträgt x = 5/4 und entspricht somit der x-Koordinate des Scheitelpunkts.

3. Berechnung der y-Koordinate:
Setze x = 5/4 in die Funktion f(x) ein:
f(5/4) = 2(5/4)^2 – 5(5/4) + 3
= 25/8 – 25/4 + 3
= -1/8

Der Scheitelpunkt hat somit die Koordinaten S(5/4, -1/8).

Anhand der Funktionsgleichung kannst du zusätzlich erkennen, dass es sich um eine nach oben geöffnete Parabel handelt, da das a vor dem quadratischen Term positiv ist. Der Scheitelpunkt stellt in diesem Fall ein Minimum dar.

Diese Methode zur Bestimmung des Scheitelpunkts durch Ableitung funktioniert jedoch nur, wenn die Funktion differenzierbar ist und eine Ableitung besitzt.

Quadratische Funktionen: Bestimmung des Scheitelpunkts mit Nullstellen

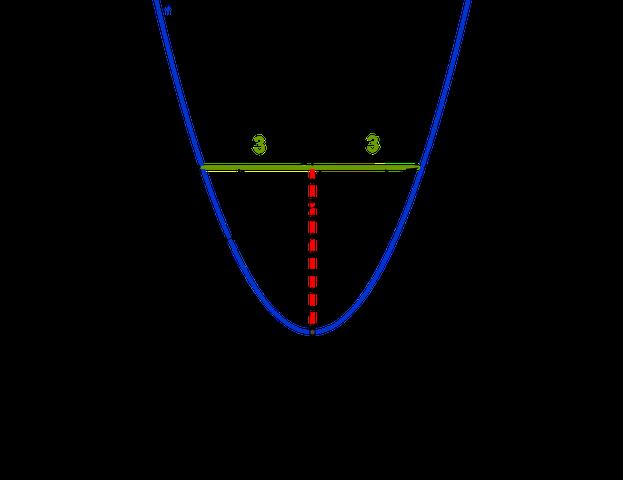
Ein Scheitelpunkt ist der tiefste oder höchste Punkt einer Parabel. Um den Scheitelpunkt einer quadratischen Funktion zu bestimmen, gibt es verschiedene Methoden. Eine davon ist die Nutzung der Nullstellen.

1. Berechnung der Nullstellen:
Um den Scheitelpunkt zu finden, müssen zuerst die Nullstellen der quadratischen Funktion berechnet werden. Dies kann durch Gleichsetzen der Funktion mit 0 erfolgen. Die x-Werte, für die die Funktion den Wert 0 annimmt, sind die Nullstellen.

Beispiel:
Die quadratische Funktion f(x) = x^2 – 4 hat die Nullstellen -2 und 2.

2. Bestimmung der x-Koordinate des Scheitelpunkts:
Da Parabeln achsensymmetrisch sind, liegt der Scheitelpunkt genau in der Mitte zwischen den beiden Nullstellen. Die x-Koordinate des Scheitelpunkts ist also gleich dem Durchschnittswert der beiden Nullstellen.

Beispiel:
Die x-Koordinate des Scheitelpunkts beträgt (0 + (-2))/2 = -1.

3. Ermittlung der y-Koordinate des Scheitelpunkts:
Um die y-Koordinate des Scheitelpunkts zu bestimmen, setzt man den x-Wert des Scheitelpunkts in die ursprüngliche Funktion ein.

Beispiel:
Setzt man x = -1 in f(x) = x^2 – 4 ein, erhält man f(-1) = (-1)^2 – 4 = 1 – 4 = -3. Die y-Koordinate des Scheitelpunkts beträgt also -3.

Der Scheitelpunkt der quadratischen Funktion f(x) = x^2 – 4 liegt somit bei S(-1|-3).

Diese Methode zur Bestimmung des Scheitelpunkts ist besonders hilfreich, wenn die Parabel Nullstellen besitzt. Durch das Berechnen der Nullstellen kann man den x-Wert des Scheitelpunkts ermitteln und anschließend den entsprechenden y-Wert durch Einsetzen in die Funktion finden.

Die quadratische Ergänzung zur Bestimmung des Scheitelpunkts

Die quadratische Ergänzung ist eine Methode zur Bestimmung des Scheitelpunkts einer quadratischen Funktion. Sie wird angewendet, wenn die Funktion nicht bereits in der Scheitelpunktform gegeben ist.

Um die quadratische Ergänzung durchzuführen, gehst du folgendermaßen vor:

1. Schreibe die Funktion in der allgemeinen Form: f(x) = ax^2 + bx + c.

2. Teile den Koeffizienten b durch 2 und quadriere das Ergebnis: (b/2)^2.

3. Addiere und subtrahiere das quadrierte Ergebnis zu der Funktion: f(x) = ax^2 + bx + (b/2)^2 – (b/2)^2 + c.

4. Fasse die ersten drei Terme zusammen und schreibe sie als Quadrat einer Binomischen Formel: f(x) = a(x + b/2a)^2 – ((b/2a)^2 – c).

5. Vereinfache den Ausdruck im letzten Schritt: f(x) = a(x + b/2a)^2 – (b^2 – 4ac)/4a.

Der Scheitelpunkt der Funktion liegt bei den Koordinaten (-b/2a, -(b^2 – 4ac)/4a).

Mit Hilfe der quadratischen Ergänzung kannst du also den Scheitelpunkt einer quadratischen Funktion bestimmen, auch wenn sie nicht in der Scheitelpunktform gegeben ist.

Beispiel:
Gegeben sei die Funktion f(x) = x^2 + 6x + 8.
1. Die allgemeine Form lautet: f(x) = x^2 + 6x + 8.

Teile den Koeffizienten b durch 2 und quadriere das Ergebnis: (6/2)^2 = 9.

Addiere und subtrahiere das quadrierte Ergebnis zur Funktion: f(x) = x^2 + 6x + 9 – 9 + 8.

Fasse die ersten drei Terme zusammen und schreibe sie als Quadrat einer Binomischen Formel: f(x) = (x + 3)^2 – (9 – 8).

Vereinfache den Ausdruck im letzten Schritt: f(x) = (x + 3)^2 -1.

Der Scheitelpunkt der Funktion liegt bei den Koordinaten (-3, -1).

Durch die quadratische Ergänzung kannst du also den Scheitelpunkt einer quadratischen Funktion bestimmen, indem du die Funktion in eine Form umwandelst, bei der der Scheitelpunkt leichter ablesbar ist.

Ein Scheitelpunkt ist der höchste oder tiefste Punkt einer Kurve und markiert den Wendepunkt. Er spielt eine wichtige Rolle in der Mathematik und Physik, da er Informationen über die Steigung und Krümmung einer Funktion liefert. Das Verständnis des Scheitelpunkts ist entscheidend, um komplexe Probleme zu lösen und Zusammenhänge besser zu verstehen.