Die Quersumme ist eine mathematische Operation, bei der die Ziffern einer Zahl addiert werden. Sie bietet eine einfache Methode, um die Summe der einzelnen Ziffern einer Zahl zu berechnen. In diesem Artikel erfahren Sie, was eine Quersumme ist und wie sie berechnet wird.
- Das mysteriöse Geschehen am 26. Juni 1284 – eine düstere Geschichte ohne Happy End
- Die Bedeutung des Namens Emilia: Geschichte, Variationen und berühmte Namensträgerinnen
- Was ist Ecstasy? Gefährliche Wirkung der Droge
- Warum hast du nicht nein gesagt: Akkorde und Melodie in unserem Leitfaden
- Stephan Sindera: Alter und Hobbys – Backgammon spielen und Ski fahren
Was ist eine Quersumme und wie berechnet man sie?
Eine Quersumme ist die Summe der Ziffernwerte einer natürlichen Zahl. Um die Quersumme zu berechnen, addiert man die einzelnen Ziffern der Zahl. Zum Beispiel ergibt die Quersumme von 24.869 die Summe der Ziffernwerte 2 + 4 + 8 + 6 + 9, also 29.
Die Quersumme spielt eine wichtige Rolle in verschiedenen mathematischen Konzepten und Regeln. Sie wird zum Beispiel bei den Teilbarkeitsregeln für die Teiler 3 und 9 verwendet. Um festzustellen, ob eine Zahl durch 3 oder 9 teilbar ist, kann man ihre Quersumme berechnen und prüfen, ob diese ebenfalls durch 3 oder 9 teilbar ist.
Um die Quersumme einer Zahl zu berechnen, schreibt man zunächst die Ziffern der Zahl auf und addiert sie anschließend zusammen. Dabei werden keine weiteren Rechenoperationen wie Addition oder Subtraktion benötigt. Die Quersumme ist somit ein einfacher Weg, um die Summe der Ziffernwerte einer Zahl zu ermitteln.
Insgesamt ist die Quersumme ein nützliches mathematisches Konzept, das in verschiedenen Bereichen Anwendung findet und dabei hilft, bestimmte Eigenschaften von Zahlen zu bestimmen.
Die Bedeutung der Quersumme in der Mathematik erklärt
Die Quersumme einer natürlichen Zahl ist die Summe der einzelnen Ziffernwerte dieser Zahl. Dabei wird jede Ziffer einzeln betrachtet und zu der Gesamtsumme addiert. Die Quersumme spielt in der Mathematik eine wichtige Rolle, insbesondere bei den Teilbarkeitsregeln für die Teiler 3 und 9.
Ein Beispiel zur Verdeutlichung: Die Quersumme von 24.869 ergibt sich durch Addition der einzelnen Ziffernwerte: 2 + 4 + 8 + 6 + 9 = 29. Bei der Zahl 158 beträgt die Quersumme 1 + 5 + 8 = 14.
Die Quersumme kann auch als Fachbegriff oder Fachwort bezeichnet werden und wird im Rahmen von Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division verwendet. Sie dient dazu, die Ziffern einer Zahl zu analysieren und bestimmte Eigenschaften oder Zusammenhänge zu erkennen.
In der Mathematik gibt es weitere Begriffe, die eng mit der Quersumme zusammenhängen. Zum Beispiel das kleinste gemeinsame Vielfache (kgV) und der größte gemeinsame Teiler (ggT). Das kgV ist das kleinste Vielfache zweier oder mehrerer Zahlen, während der ggT der größte gemeinsame Teiler dieser Zahlen ist. Um das kgV oder den ggT zu berechnen, kann unter anderem die Primfaktorzerlegung verwendet werden.
Die Bedeutung der Quersumme liegt also darin, dass sie eine Methode bietet, um die Ziffern einer Zahl zu analysieren und bestimmte mathematische Zusammenhänge zu erkennen. Sie ist insbesondere bei Teilbarkeitsregeln und Rechenoperationen von Bedeutung.
Quersumme: Definition und Anwendungsbeispiele
Die Quersumme einer natürlichen Zahl ist die Summe der Ziffernwerte dieser Zahl. Um die Quersumme zu berechnen, werden die einzelnen Ziffern der Zahl addiert. Zum Beispiel ergibt die Quersumme von 24.869 die Summe der Ziffernwerte 2 + 4 + 8 + 6 + 9, also 29.
Die Quersumme spielt in der Mathematik eine wichtige Rolle, insbesondere bei den Teilbarkeitsregeln für die Teiler 3 und 9. Eine Zahl ist genau dann durch 3 oder durch 9 teilbar, wenn ihre Quersumme ebenfalls durch 3 bzw. durch 9 teilbar ist.
Ein Anwendungsbeispiel für die Quersumme ist das Überprüfen von Kreditkartennummern. Hierbei wird mithilfe der Quersummenregel überprüft, ob eine Kreditkartennummer gültig ist oder nicht.
Zusammenfassend kann man sagen, dass die Quersumme einer natürlichen Zahl die Summe ihrer Ziffernwerte ist und in verschiedenen mathematischen Kontexten Anwendung findet.
Wie die Quersumme bei Teilbarkeitsregeln hilft
Die Quersumme spielt eine wichtige Rolle bei den Teilbarkeitsregeln für die Teiler 3 und 9. Durch die Berechnung der Quersumme einer Zahl kann man feststellen, ob diese Zahl durch 3 oder 9 teilbar ist.
Um zu überprüfen, ob eine Zahl durch 3 teilbar ist, berechnet man die Quersumme dieser Zahl. Ist die Quersumme selbst durch 3 teilbar, so ist auch die Ausgangszahl durch 3 teilbar. Zum Beispiel ist die Zahl 24.869 gegeben. Die Quersumme von 24.869 beträgt: 2 + 4 + 8 + 6 + 9 = 29. Da die Quersumme nicht durch 3 teilbar ist, ist auch die Ausgangszahl nicht durch 3 teilbar.
Für die Teilbarkeit durch 9 gilt dasselbe Prinzip. Ist die Quersumme einer Zahl durch 9 teilbar, so ist auch diese Zahl selbst durch 9 teilbar. Nehmen wir als Beispiel wieder die Zahl 24.869. Die Quersumme beträgt hier ebenfalls: 2 + 4 +8 +6 +9 =29. Da auch hier die Quersumme nicht durch 9 teilbar ist, lässt sich schließen, dass auch die Ausgangszahl nicht durch 9 teilbar ist.
Die Berechnung der Quersumme ermöglicht somit eine schnelle Überprüfung der Teilbarkeit einer Zahl durch sowohl den Teiler drei als auch den Teiler neun in der Mathematik.
Mathematische Fachbegriffe: Was ist eine Quersumme?
Eine Quersumme ist die Summe der Ziffernwerte einer natürlichen Zahl. Um die Quersumme zu berechnen, werden die einzelnen Ziffern addiert. Zum Beispiel ergibt die Quersumme von 24.869 die Summe der Ziffernwerte 2 + 4 + 8 + 6 + 9, also 29.
Die Quersumme spielt in der Mathematik eine wichtige Rolle, insbesondere bei den Teilbarkeitsregeln für die Teiler 3 und 9. Eine Zahl ist genau dann durch 3 oder durch 9 teilbar, wenn ihre Quersumme ebenfalls durch 3 bzw. durch 9 teilbar ist.
Die Berechnung der Quersumme wird häufig als einfache Übungsaufgabe verwendet, um das Rechnen mit Zahlen zu trainieren. Sie kann auch dazu genutzt werden, um bestimmte Eigenschaften von Zahlen zu untersuchen oder mathematische Rätsel zu lösen.
Insgesamt ist die Quersumme ein grundlegender Begriff in der Mathematik, der sowohl in einfachen Rechenoperationen als auch in komplexeren mathematischen Fragestellungen Anwendung findet.
Praktische Anwendung der Quersumme in Matheaufgaben
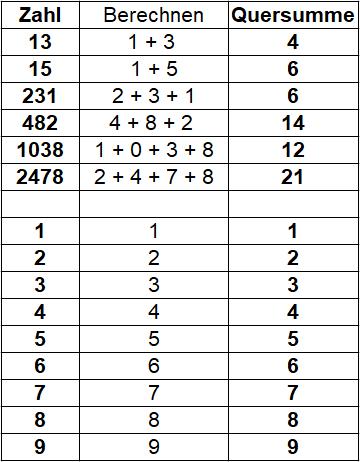
Die Quersumme einer Zahl wird oft in verschiedenen mathematischen Aufgaben verwendet. Zum Beispiel kann die Quersumme bei der Überprüfung von Teilbarkeitsregeln für die Teiler 3 und 9 eine wichtige Rolle spielen.
Ein praktisches Anwendungsbeispiel ist die Bestimmung des kleinsten gemeinsamen Vielfachen (kgV) zweier Zahlen. Um das kgV zu berechnen, zerlegt man beide Zahlen in ihre Primfaktoren und nimmt jeweils den höchsten Exponenten für jeden Primfaktor. Dann multipliziert man diese Primfaktoren miteinander, um das kgV zu erhalten.
Die Quersumme kann auch verwendet werden, um bestimmte Muster oder Eigenschaften von Zahlen zu erkennen. Zum Beispiel kann man durch die Berechnung der Quersumme einer Zahl feststellen, ob sie durch 3 oder 9 teilbar ist. Ist die Quersumme einer Zahl durch 3 oder 9 teilbar, so ist auch die Zahl selbst durch 3 oder 9 teilbar.
In Matheaufgaben kann die Quersumme auch dazu verwendet werden, um bestimmte Eigenschaften von Zahlenreihen oder -folgen zu analysieren. Durch die Berechnung der Quersummen einzelner Glieder einer Reihe oder Folge können Muster erkannt und Zusammenhänge aufgedeckt werden.
Die Quersumme ist also ein nützliches Werkzeug in der Mathematik, um verschiedene Aufgaben zu lösen und Eigenschaften von Zahlen zu untersuchen.
Die Quersumme einer Zahl ist die Summe ihrer einzelnen Ziffern. Sie dient als mathematisches Werkzeug, um Eigenschaften von Zahlen zu analysieren und zu berechnen. Die Quersumme kann verwendet werden, um die Teilbarkeit einer Zahl zu überprüfen oder um bestimmte Muster in Zahlenreihen zu identifizieren. Sie ist eine einfache und effektive Methode, um das Verständnis von Zahlen und ihre Beziehungen zueinander zu verbessern.