Ein Ortsvektor ist ein mathematisches Konzept, das verwendet wird, um die Position eines Punktes im Raum zu beschreiben. Er besteht aus einer geordneten Reihe von Koordinaten und gibt an, wie weit und in welche Richtung ein Punkt von einem bestimmten Bezugspunkt entfernt ist. Ortsvektoren sind sowohl in der Geometrie als auch in der Physik von großer Bedeutung. Sie ermöglichen es uns, Objekte im Raum zu lokalisieren und ihre Bewegungen zu verfolgen.
- Die Bedeutung des Namens Isabel – eine göttliche Schönheit
- Was bedeutet es, extrovertiert zu sein?
- Wie lange sind alte Pkw-Führerscheine gültig? Welche Dokumente für Umtausch benötigt?
- Vogeltränken selber machen: Dekorative Wasserstellen für Vögel
- Wann wurde die Wehrpflicht abgeschafft? Die Abschaffung der Wehrpflicht erfolgte im Jahr 2011.
Die Bedeutung und Eigenschaften eines Ortsvektors
Ein Ortsvektor ist ein Vektor, der vom Ursprung zu einem bestimmten Punkt im Raum zeigt. Er hat die gleichen Koordinaten wie der Punkt selbst. Ein Beispiel für einen Ortsvektor ist der Vektor OA→=(25−3)\overrightarrow{OA}=\begin{pmatrix}2\\5\\-3\end{pmatrix}OA=25−3 zum Punkt A(2∣5∣−3)A(2\vert5\vert-3)A(2∣5∣−3).
Der Ortsvektor wird oft mit einem Pfeil über dem Buchstaben des Punktes dargestellt, z.B. A⃗\vec{A}A für den Ortsvektor zu Punkt A. Es ist auch üblich, den entsprechenden Kleinbuchstaben zu verwenden, z.B. a⃗\vec{a}a für OA→\overrightarrow{OA}OA oder p⃗\vec{p}p für OP→\overrightarrow{OP}OP.
Wenn man den Gegenvektor haben möchte, also den Vektor vom Punkt zum Ursprung, muss man einfach die Vorzeichen des Vektors umdrehen. Das bedeutet, statt OA→\overrightarrow{OA}OA rechnet man mit −A→-\overrightarrow{A}-A.
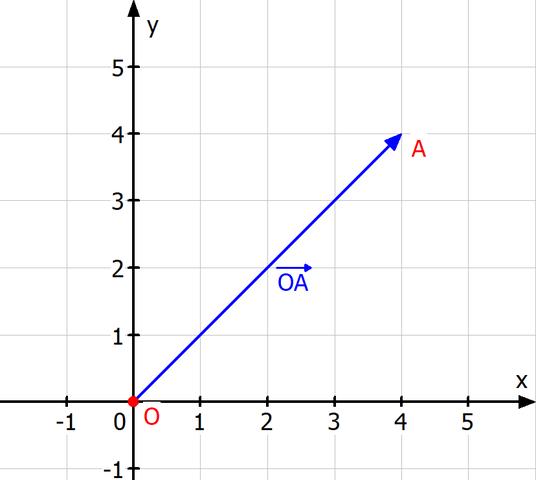
Ortsvektoren und Vektorketten können verwendet werden, um Koordinaten im Raum zu berechnen. Im Koordinatensystem ist der Punkt A(3∣6)A\left(3|6\right)A(3∣6) eingezeichnet. Der zugehörige Ortsvektor A⃗\vec{A}A verbindet den Ursprung mit dem Punkt A und wird durch (36)\begin{pmatrix}3\\6\end{pmatrix}(36) ausgedrückt.
Ein Ortsvektor ist also ein nützliches Konzept in der Vektorrechnung, um Punkte im Raum zu beschreiben und Berechnungen durchzuführen.
Ein Ortsvektor: Definition und Anwendung
Definition eines Ortsvektors
Ein Ortsvektor ist ein Vektor, der vom Ursprung eines Koordinatensystems zu einem bestimmten Punkt zeigt. Dieser Vektor hat die gleichen Koordinaten wie der Punkt selbst. Zum Beispiel ist der Ortsvektor zum Punkt A(2∣5∣−3)OA→=(25−3)\overrightarrow{OA}=\begin{pmatrix}2\\5\\-3\end{pmatrix}OA=25−3.
Anwendung von Ortsvektoren
Ortsvektoren werden häufig verwendet, um Positionen im Raum zu berechnen. Sie ermöglichen es uns, Punkte im dreidimensionalen Koordinatensystem präzise zu beschreiben und mathematisch zu behandeln. Durch die Verwendung von Vektorketten können wir auch komplexe Berechnungen durchführen.
Es ist üblich, den Ortsvektor mit einem Kleinbuchstaben zu bezeichnen, z.B. a⃗\vec aa für OA→\overrightarrow{OA}OA oder p⃗\vec pp für OP→\overrightarrow{OP}OP.
Gegenvektor
Wenn wir den Gegenvektor haben möchten, also den Vektor vom Punkt zum Ursprung, müssen wir einfach die Vorzeichen des Vektors umdrehen. Anstatt mit A→\overrightarrow AA zu rechnen, verwenden wir −A→-\overrightarrow A−A.
Es gibt noch viele weitere interessante Inhalte zum Thema Ortsvektoren auf Serlo.org! Melde dich an, um diese Funktion zu nutzen und mehr über dieses Thema zu erfahren.
Alles, was du über Ortsvektoren wissen musst
Definition und Eigenschaften von Ortsvektoren
Ein Ortsvektor ist ein Vektor, der vom Ursprung eines Koordinatensystems zu einem bestimmten Punkt zeigt. Er hat die gleichen Koordinaten wie der Punkt selbst. Der Ortsvektor zum Punkt A(2∣5∣−3) zum Beispiel ist OA→=(25−3)\overrightarrow{OA}=\begin{pmatrix}2\\5\\-3\end{pmatrix}. Man kann den Ortsvektor auch durch den Buchstaben des Punktes darstellen, z.B. a⃗\vec aa für OA→\overrightarrow{OA}OA.
Gegenvektor und Berechnung von Koordinaten im Raum
Möchte man den Gegenvektor haben, also den Vektor vom Punkt zum Ursprung, muss man nur die Vorzeichen des Vektors umdrehen. Anstatt mit A→\overrightarrow AA rechnet man dann mit −A→-\overrightarrow A−A. Mithilfe von Ortsvektoren und Vektorketten können Koordinaten im Raum berechnet werden.
Weitere Informationen über Serlo.org
Serlo.org ist nach einem Kloster in Nepal benannt, wo der Gründer die Idee für eine freie Lernplattform hatte. Auf Serlo sind Themen so aufbereitet, dass du sie besonders leicht selbstständig lernen kannst. Hinter serlo.org stehen viele engagierte Menschen, die Bildung besser und gerechter machen wollen. Du kannst auch Teil der Serlo Community werden und mitmachen.
Der Ursprungspunkt und der Ortsvektor im Raum
Was ist ein Ortsvektor?
Ein Ortsvektor ist ein Vektor, der vom Ursprung eines Koordinatensystems zu einem bestimmten Punkt im Raum zeigt. Er hat die gleichen Koordinaten wie der Punkt selbst. Der Ortsvektor zum Punkt A(2∣5∣−3) ist beispielsweise OA→=(25−3) oder in Vektorschreibweise \begin{pmatrix}2\\5\\-3\end{pmatrix}. Man kann den Ortsvektor auch als A→\overrightarrow{A} oder a⃗\vec{a} abkürzen.
Der Gegenvektor
Möchte man den Gegenvektor, also den Vektor vom Punkt zum Ursprung, haben, muss man nur die Vorzeichen des Vektors umdrehen. Statt A→\overrightarrow{A} rechnet man dann mit −A→-\overrightarrow{A}. Der Gegenvektor von OA→ wäre also -OA→.
Berechnung von Koordinaten im Raum
Mit Hilfe von Ortsvektoren und Vektorketten können Koordinaten im Raum berechnet werden. Im Koordinatensystem ist der Punkt A(3∣6) eingezeichnet. Der zugehörige Ortsvektor A⃗\vec{A} verbindet den Ursprung mit dem Punkt A und wird durch (36)\begin{pmatrix}3\\6\end{pmatrix} ausgedrückt.
Wie man einen Ortsvektor berechnet und interpretiert
Berechnung eines Ortsvektors
Ein Ortsvektor ist ein Vektor, der vom Ursprung eines Koordinatensystems zu einem bestimmten Punkt zeigt. Um einen Ortsvektor zu berechnen, verwendet man die Koordinaten des Punktes selbst. Der Ortsvektor zum Punkt A(2∣5∣−3) wird beispielsweise durch den Vektor OA→=(25−3) dargestellt. Dieser Vektor hat die gleichen Koordinaten wie der Punkt A.
Interpretation eines Ortsvektors
Der Ortsvektor verbindet den Ursprung des Koordinatensystems mit einem bestimmten Punkt im Raum. Er gibt die Richtung und Länge der Verbindungslinie zwischen diesen beiden Punkten an. Die Komponenten des Ortsvektors entsprechen den Koordinaten des Punktes.
Durch die Verwendung von Ortsvektoren können verschiedene Berechnungen im Raum durchgeführt werden, wie zum Beispiel das Berechnen von Abständen zwischen Punkten oder das Bestimmen von Winkeln zwischen Vektoren.
Es ist auch möglich, den Gegenvektor zu einem bestimmten Punkt zu berechnen, indem man einfach die Vorzeichen der Komponenten des Vektors umdreht. Der Gegenvektor zeigt dann vom Punkt zurück zum Ursprung.
Insgesamt sind Ortsvektoren eine wichtige mathematische Konzept in der Geometrie und Physik, um Positionen im Raum darzustellen und Berechnungen durchzuführen.
Die Rolle von Ortsvektoren bei der Koordinatenbestimmung im Raum
Definition und Eigenschaften von Ortsvektoren
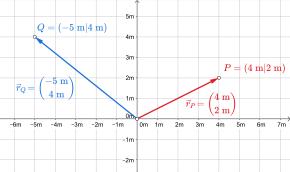
Ein Ortsvektor ist ein Vektor, der vom Ursprung eines Koordinatensystems zu einem bestimmten Punkt im Raum zeigt. Er hat die gleichen Koordinaten wie der Punkt selbst. Zum Beispiel ist der Ortsvektor zum Punkt A(2∣5∣−3) durch den Vektor OA→=(25−3)\overrightarrow{OA}=\begin{pmatrix}2\\5\\-3\end{pmatrix}OA=25−3 gegeben. Oft wird statt OA→\overrightarrow{OA}OA auch die verkürzte Schreibweise A→\overrightarrow AA verwendet.
Berechnung von Koordinaten im Raum mit Hilfe von Ortsvektoren und Vektorketten
Ortsvektoren spielen eine wichtige Rolle bei der Berechnung von Koordinaten im Raum. Durch Addition oder Subtraktion von Vektoren können neue Punkte im Raum bestimmt werden. Wenn beispielsweise der Punkt A(3∣6)A\left(3|6\right)A(3∣6) gegeben ist, kann der zugehörige Ortsvektor A⃗\vec{A}A den Ursprung mit dem Punkt A verbinden und wird durch (36)\begin{pmatrix}3\\6\end{pmatrix}(36) ausgedrückt.
Es ist auch möglich, den Gegenvektor zu berechnen, indem man die Vorzeichen des Vektors umdreht. Der Gegenvektor von A→\overrightarrow{A}A ist dann -A→-\overrightarrow{A}-A, der vom Punkt A zum Ursprung zeigt.
Durch die Verwendung von Ortsvektoren und Vektorketten können somit Koordinaten im Raum berechnet werden und geometrische Probleme gelöst werden.
Der Ortsvektor ist ein mathematisches Konzept, das zur Beschreibung der Position eines Punktes im Raum verwendet wird. Er besteht aus den Koordinaten des Punktes und kann sowohl für einzelne Punkte als auch für Richtungen und Abstände verwendet werden. Durch die Verwendung von Ortsvektoren können komplexe geometrische Probleme effizient gelöst werden.