Einführung in den Logarithmus: Bedeutung und Anwendung

Ein Logarithmus ist eine mathematische Funktion, die dazu dient, exponentielle Zusammenhänge zu beschreiben und zu lösen. Er wird verwendet, um die Potenz einer Zahl zur Basis einer anderen Zahl zu finden. Diese Funktion spielt eine wichtige Rolle in verschiedenen Bereichen wie der Algebra, der Analysis und der Statistik. In diesem Artikel werden wir den Begriff des Logarithmus genauer untersuchen und seine Anwendungen verstehen lernen.

Einführung in den Logarithmus: Was ist ein Logarithmus und wie funktioniert er?

Paragraph 1:

Ein Logarithmus ist eine mathematische Funktion, die dir hilft, exponentielle Beziehungen umzukehren. Wenn du beispielsweise wissen möchtest, welchen Exponenten du auf eine bestimmte Zahl setzen musst, um eine andere Zahl zu erhalten, kannst du den Logarithmus verwenden. Der Logarithmus gibt dir das Ergebnis des Exponenten zurück.

Paragraph 2:

Der Logarithmus wird mit dem Symbol „log“ abgekürzt und hat zwei Hauptkomponenten: die Basis und den Wert. Die Basis ist die Zahl, mit der multipliziert wird, während der Wert das Ergebnis der Multiplikation ist. Um den Exponenten zu berechnen, musst du den Logarithmus verwenden.

Paragraph 3:

Es gibt verschiedene Arten von Logarithmen, wie den natürlichen Logarithmus (ln), den binären Logarithmus (log2) und den dekadischen Logarithmus (log10). Jeder dieser Logarithmen hat eine spezifische Basis und kann verwendet werden, um unterschiedliche exponentielle Beziehungen zu lösen. Es ist wichtig zu beachten, dass der Wert des Arguments im logarithmischen Ausdruck positiv sein muss und die Basis nicht gleich eins sein darf.

– Der natürliche Logarithmus (ln) verwendet die Eulersche Zahl e als Basis.
– Der binäre Logarithmus (log2) hat die Basis 2.
– Der dekadische Logarithmus (log10) verwendet die Basis 10.

Die Verwendung des Logarithmus ist besonders nützlich beim Lösen von Gleichungen mit exponentiellen Beziehungen und kann in vielen Bereichen der Mathematik, Wissenschaft und Technologie angewendet werden.

Anwendung des Logarithmus: Wie kann der Logarithmus bei Berechnungen helfen?

1. Berechnung von Potenzen und Exponenten

Der Logarithmus kann verwendet werden, um Potenzen und Exponenten zu berechnen. Wenn du beispielsweise wissen möchtest, wie oft du eine Zahl mit sich selbst multiplizieren musst, um ein bestimmtes Ergebnis zu erhalten, kannst du den Logarithmus verwenden. Der Logarithmus gibt dir dann den Exponenten an, den du benötigst.

2. Lösung von Gleichungen

Der Logarithmus kann auch bei der Lösung von Gleichungen helfen, insbesondere wenn die gesuchte Variable im Exponenten steht. Durch Anwendung des Logarithmus auf beide Seiten der Gleichung kannst du die Variable isolieren und lösen.

3. Verwendung spezieller Logarithmen

Es gibt verschiedene Arten von speziellen Logarithmen, wie den natürlichen Logarithmus (ln) mit Basis e oder den binären Logarithmus (log Basis 2). Diese speziellen Logarithmen haben ihre eigenen Anwendungsgebiete und können in verschiedenen Bereichen der Mathematik und Informatik eingesetzt werden.

– Der natürliche Logarithmus (ln) wird verwendet, wenn man nach einem Exponenten zur Basis e sucht.
– Der binäre Logarithmus (log Basis 2) wird verwendet, wenn man nach einem Exponenten zur Basis 2 sucht.
– Der dekadische Logarithmus (log Basis 10) wird häufig in Berechnungen verwendet, bei denen die Basis 10 relevant ist.

Diese speziellen Logarithmen haben ähnliche Regeln und Anwendungen wie der allgemeine Logarithmus, unterscheiden sich jedoch in ihrer Basis und Schreibweise.

Zusammenfassend kann gesagt werden, dass der Logarithmus bei verschiedenen Berechnungen helfen kann, insbesondere bei Potenzen, Exponenten und Gleichungen. Die Verwendung spezieller Logarithmen ermöglicht eine präzisere Anpassung an bestimmte Berechnungsanforderungen.

Eigenschaften des Logarithmus: Regeln und Besonderheiten beim Rechnen mit dem Logarithmus

Rechenregeln für den Logarithmus:

– Der Logarithmus von einer Produktzahl ist gleich der Summe der Logarithmen der Faktoren: log(ab) = log(a) + log(b)
– Der Logarithmus von einem Quotienten ist gleich der Differenz der Logarithmen des Zählers und des Nenners: log(a/b) = log(a) – log(b)
– Der Logarithmus einer Potenz ist gleich dem Produkt des Exponenten und dem Logarithmus der Basis: log(a^b) = b * log(a)

Besonderheiten beim Berechnen mit dem Logarithmus:

– Die Basis des Logarithmus muss eine positive Zahl sein, genauso wie der sogenannte Numerus.
– Negative Zahlen dürfen nicht als Argument in den Logarithmus eingesetzt werden.
– Die Basis Eins ist ausgeschlossen, es gilt also b ≠ 1.
– Der Logarithmus von Null ist nicht definiert, unabhängig von der Basis.
– Der natürliche Logarithmus (ln) hat als Basis die Eulersche Zahl e und wird verwendet, um nach einem Exponenten zu e zu suchen.
– Ein logarithmischer Ausdruck mit Basis 2 wird auch als binärer Logarithmus bezeichnet und wird verwendet, um den Exponenten x zur Basis 2 zu finden.
– Der dekadische Logarithmus hat als Basis 10 und wird manchmal als lg oder einfach nur als log ohne Angabe der Basis geschrieben.

Das sind einige wichtige Regeln und Besonderheiten beim Rechnen mit dem Logarithmus. Weitere Details und Beispiele findest du in unserem Video zu den Logarithmus Regeln.

Der natürliche Logarithmus: Erklärung und Anwendung des ln

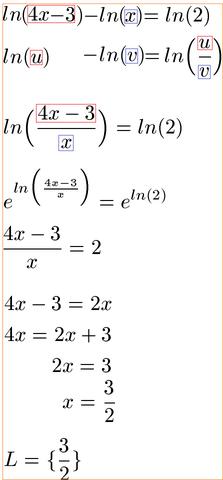
Was ist der natürliche Logarithmus?

Der natürliche Logarithmus, auch als ln abgekürzt, ist eine spezielle Form des Logarithmus. Er hat die Eulersche Zahl e als Basis. Der natürliche Logarithmus wird verwendet, um den Exponenten zu berechnen, der benötigt wird, um die Eulersche Zahl e zu einer bestimmten Zahl zu erheben.

Anwendung des natürlichen Logarithmus

Der natürliche Logarithmus findet in verschiedenen Bereichen Anwendung. In der Mathematik wird er zum Lösen von Gleichungen verwendet, bei denen der Exponent im Logarithmus steht. Er ermöglicht es uns, den Wert von x zu finden, wenn wir wissen möchten, welcher Exponent benötigt wird, um die Eulersche Zahl e zu einer bestimmten Zahl zu erheben.

Des Weiteren spielt der natürliche Logarithmus eine wichtige Rolle in der Analysis und in vielen naturwissenschaftlichen Bereichen wie Physik oder Biologie. Er findet beispielsweise Anwendung bei exponentiellem Wachstum oder Zerfall.

Zusammenfassend kann gesagt werden, dass der natürliche Logarithmus ein wichtiges mathematisches Konzept ist und vielfältige Anwendungen hat. Es lohnt sich daher, ihn genauer zu verstehen und seine Rechenregeln anzuwenden.

Der binäre Logarithmus: Verwendung und Berechnung des log Basis 2

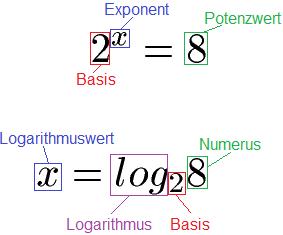
Was ist der binäre Logarithmus?

Der binäre Logarithmus, auch bekannt als logarithmus dualis oder logarithmus zur Basis 2, ist eine spezielle Form des Logarithmus. Er wird verwendet, um den Exponenten zu berechnen, zu dem die Zahl 2 potenziert werden muss, um einen bestimmten Wert zu erhalten. Der binäre Logarithmus hat viele Anwendungen in der Informatik und der Informationstechnologie.

Wie berechnet man den binären Logarithmus?

Um den binären Logarithmus zu berechnen, verwendest du die Funktion log zur Basis 2 auf einem Taschenrechner oder in einer mathematischen Software. Du gibst einfach die Zahl ein, von der du den Exponenten zur Basis 2 wissen möchtest, und drückst die entsprechende Taste. Das Ergebnis gibt dir den Exponenten x zurück.

Schreibweisen für den binären Logarithmus

Es gibt verschiedene Schreibweisen für den binären Logarithmus. Die ausgeschriebene Variante mit „log Basis 2“ ist am häufigsten anzutreffen. Es gibt jedoch auch Abkürzungen wie „lb“ oder „ld“, die ebenfalls für den binären Logarithmus stehen. Diese Schreibweisen sind in der Informatik weit verbreitet.

– Der binäre Logarithmus wird verwendet, um den Exponenten zu berechnen, zu dem die Zahl 2 potenziert werden muss.
– Du kannst ihn mit der Funktion log zur Basis 2 auf einem Taschenrechner oder in mathematischer Software berechnen.
– Es gibt verschiedene Schreibweisen für den binären Logarithmus, wie „log Basis 2“, „lb“ oder „ld“.

Der dekadische Logarithmus: Bedeutung und Anwendung des log Basis 10

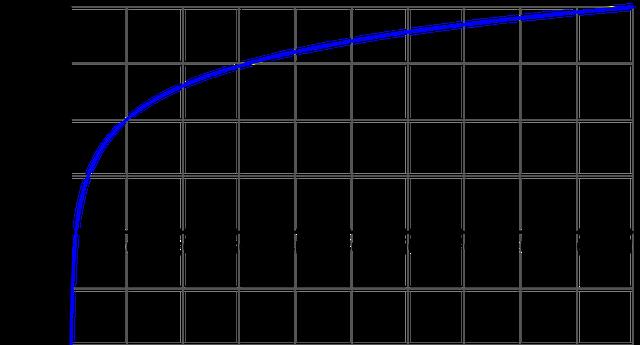
Bedeutung des dekadischen Logarithmus

Der dekadische Logarithmus, auch als log zur Basis 10 bezeichnet, ist eine spezielle Form des Logarithmus. Er gibt an, welche Zahl du in den Exponenten von 10 schreiben musst, um einen bestimmten Wert zu erhalten. Der dekadische Logarithmus wird häufig verwendet, um Zahlen mit vielen Nullen oder sehr großen Zahlen übersichtlicher darzustellen. Durch die Anwendung des dekadischen Logarithmus können komplexe Berechnungen vereinfacht werden.

Anwendung des dekadischen Logarithmus

Der dekadische Logarithmus findet in verschiedenen Bereichen Anwendung. Zum Beispiel wird er in der Geometrie verwendet, um den Maßstab von Karten und Plänen anzugeben. In der Physik wird der dekadische Logarithmus genutzt, um Größenordnungen zu bestimmen und Messwerte zu vergleichen. Auch in der Informatik spielt der dekadische Logarithmus eine wichtige Rolle bei der Umrechnung von Binär- in Dezimalzahlen.

• Um den dekadischen Logarithmus einer Zahl zu berechnen, kannst du entweder einen Taschenrechner verwenden oder auf logarithmische Tabellen zurückgreifen.
• Der Wert des dekadischen Logarithmus ist immer eine reelle Zahl.
• Es gelten die üblichen Rechenregeln für den logarithmischen Ausdruck.
• Wenn der Wert des dekadischen Logarithmus negativ ist, bedeutet dies, dass die Ausgangszahl kleiner als 1 ist.

Der dekadische Logarithmus ist ein wichtiges mathematisches Konzept und findet in vielen Bereichen Anwendung. Durch seine Nutzung können komplexe Berechnungen vereinfacht und Zahlen übersichtlicher dargestellt werden.

Zusammenfassend ist ein Logarithmus eine mathematische Funktion, die das Verhältnis zwischen einer Zahl und einer Basis darstellt. Er wird verwendet, um exponentielle Wachstums- oder Abnahmeprozesse umzukehren und bietet eine effektive Methode zur Vereinfachung komplexer Berechnungen. Das Verständnis des Logarithmus ist für viele wissenschaftliche und technische Anwendungen unerlässlich.