Ein Kehrwert ist eine mathematische Bezeichnung für den umgekehrten Wert einer Zahl oder eines Bruchs. Er wird durch das Umkehren des Zählers und des Nenners gebildet. Der Kehrwert einer Zahl x ist also 1/x, während der Kehrwert eines Bruchs a/b b/a ist. Der Kehrwert kann verwendet werden, um Divisionen in Multiplikationen umzuwandeln und ermöglicht es uns, mathematische Operationen effizienter durchzuführen.
Was ist ein Kehrwert und wie berechnet man ihn?
Der Kehrwert einer Zahl ist die Zahl, mit der man sie multiplizieren kann, um das Ergebnis 1 zu erhalten. Der Kehrwert wird verwendet, um Divisionen durchzuführen und Brüche zu vereinfachen. Um den Kehrwert einer Zahl zu berechnen, wird der Zähler und der Nenner des Bruchs vertauscht.
Beispiel: Der Kehrwert von 3/4 ist 4/3. Wenn wir 3/4 mit seinem Kehrwert multiplizieren, erhalten wir 1.
Um den Kehrwert einer ganzen Zahl zu berechnen, wird der Nenner auf 1 gesetzt. Dadurch ändert sich der Wert der Zahl nicht. Anschließend werden Zähler und Nenner vertauscht.
Beispiel: Der Kehrwert von 5 ist 1/5. Wenn wir 5 mit seinem Kehrwert multiplizieren, erhalten wir wiederum 1.
In der Potenzrechnung entspricht der Kehrwert einer Potenz dem gleichen Ausdruck, nur dass das Vorzeichen des Exponenten negativ wird.
Beispiel: Der Kehrwert von 5^3 ist 1/5^3 oder auch 1/125.
Der Kehrwert eines Bruchs wird als „Kehrbruch“ bezeichnet und entsteht durch Vertauschen von Zähler und Nenner.
Zusammenfassend lässt sich sagen, dass der Kehrwert einer Zahl eine wichtige Rolle bei Divisionen und Vereinfachungen von Brüchen spielt. Er ermöglicht es uns, komplexe Berechnungen zu vereinfachen und das Ergebnis zu erhalten.
Die Bedeutung des Kehrwerts und wie man ihn bildet

Der Kehrwert einer Zahl ist diejenige Zahl, die mit der gegebenen Zahl multipliziert 1 ergibt. Ausgenommen davon ist die Zahl 0. Der Kehrwert wird auch als Kehrbruch bezeichnet. Um den Kehrwert eines Bruchs zu bilden, werden Zähler und Nenner vertauscht. Dadurch erhält man den Kehrbruch des Bruchs.
Beispiel: Der Kehrwert des Bruchs \(\frac{2}{3}\) ist \(\frac{3}{2}\).
Um den Kehrwert einer ganzen Zahl zu bilden, wird der Nenner gleich 1 gesetzt und somit eine Bruchzahl erstellt. Anschließend werden Zähler und Nenner vertauscht, um den Kehrbruch zu erhalten.
Beispiel: Der Kehrwert der Zahl 5 ist \(\frac{1}{5}\).
Der Kehrwert einer Potenz mit Basis \(a\) und Exponent \(b\) ist gegeben durch \(a^{-b}\). Dabei gilt die Rechenregel \(a^{-b} = \frac{1}{a^b}\).
In der Bruchrechnung wird der Kehrwert verwendet, um eine Division zweier Brüche durchzuführen. Dazu wird der erste Bruch mit dem Kehrbruch des zweiten Bruchs multipliziert.
Zusammenfassend kann gesagt werden, dass der Kehrwert einer Zahl oder eines Bruchs diejenige Zahl bzw. derjenige Bruch ist, dessen Produkt mit dem Ausgangswert immer 1 ergibt. Um den Kehrwert zu bilden, werden Zähler und Nenner vertauscht.
Der Kehrwert: Definition und Berechnung
Der Kehrwert einer beliebigen Zahl \(x\) ist diejenige Zahl, die mit \(x\) multipliziert \(1\) ergibt. Dabei wird die Zahl \(0\) ausgeschlossen.
In einigen Definitionen oder Aufgaben findest Du eine andere Schreibweise für den Bruch \(\frac{1}{x}\). Du kannst diesen auch als \(x^{-1}\) angeben. Somit gibt es zu jedem Bruch einen „Gegenspieler“, dessen Produkt genau \(1\) ergibt. Der Kehrwert eines Bruches wird als Kehrbruch bezeichnet.
Um den Kehrbruch zu bilden, vertauschst Du den Zähler und den Nenner des angegebenen Bruches: Die Zahl über dem Bruchstrich wird mit der Zahl unter dem Bruchstrich vertauscht. Dadurch erhältst Du den Kehrwert des Bruches.
Beispiel:
\[\frac{{\color{bl}a}}{{\color{gr}b}}\rightarrow\frac{{\color{gr}b}}{{\color{bl}a}}\]
Du möchtest den Kehrwert des Bruches \(\frac{2}{3}\) bilden. Dazu vertauschst Du die beiden Zahlen des Bruches und erhältst dadurch den Kehrwert:
\[\frac{{\color{bl}2}}{{\color{gr}3}}\rightarrow\frac{{\color{gr}3}}{{\color{bl}2}}\]
Um den Kehrwert aus einer ganzen Zahl zu bilden, veränderst Du die angegebene ganze Zahl in eine Bruchzahl. Dafür setzt Du den Nenner gleich \(1\) und erhältst damit eine Bruchzahl, deren Wert immer noch \(5\) ist.
\[{\color{bl}5}\rightarrow\frac{{\color{bl}5}}{1}\]
Aus diesem neuen Bruch kannst Du nun den Kehrwert bilden, indem Du die Zahlen des Bruches vertauschst.
\[\frac{{\color{bl}5}}{{\color{gr}1}} \rightarrow \frac{{\color{gr}1}}{{\color{bl}5}}\]
Den Kehrwert einer Potenz erhältst Du, indem sich das Vorzeichen des Exponenten tauscht. Im Allgemeinen ist der Kehrwert einer Potenz \(a^b\) mit Basis \(a\) und Exponenten \(b\) gegeben durch \(a^{-b}\). Dabei gilt die Rechenregel \(a^{-b} = \frac{1}{a^b}\).
In der Bruchrechnung benötigst Du den Kehrwert eines Bruches, um eine Division zweier Brüche durchzuführen. Dazu multiplizierst Du den ersten Bruch mit dem Kehrwert des zweiten Bruches.
Speicher die Erklärung jetzt ab und lies sie, wenn Du Zeit hast. Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken. Nie wieder prokrastinieren mit unseren Lernerinnerungen!
Alles, was du über den Kehrwert wissen musst
Was ist der Kehrwert?
Der Kehrwert einer beliebigen Zahl x ist diejenige Zahl, die mit x multipliziert 1 ergibt. Dabei wird die Zahl 0 ausgeschlossen. In einigen Definitionen oder Aufgaben findest du eine andere Schreibweise für den Bruch \(\frac{1}{x}\), nämlich \(x^{-1}\). Somit gibt es zu jedem Bruch einen „Gegenspieler“, dessen Produkt genau 1 ergibt.
Wie berechnet man den Kehrwert?
Um den Kehrwert eines Bruchs zu bilden, vertauscht man einfach den Zähler und den Nenner des Bruchs. Dadurch erhält man den Kehrwert des Bruchs. Möchte man den Kehrwert einer ganzen Zahl berechnen, wandelt man diese zuerst in eine Bruchzahl um, indem man einen Nenner mit dem Wert 1 hinzufügt.
Anwendung des Kehrwerts
Der Kehrwert wird oft verwendet, um Divisionen von Brüchen durchzuführen. Dazu multipliziert man einfach den ersten Bruch mit dem Kehrwert des zweiten Bruchs. Das Produkt des Ausgangsbruchs und seines Kehrbruchs ergibt immer 1.
Zusammenfassend kann gesagt werden, dass der Kehrwert einer Zahl diejenige Zahl ist, die mit ihr multipliziert 1 ergibt. Der Kehrwert eines Bruchs wird gebildet, indem man Zähler und Nenner vertauscht. Der Kehrwert wird unter anderem bei der Division von Brüchen angewendet, indem man den ersten Bruch mit dem Kehrwert des zweiten Bruchs multipliziert.
Der Kehrwert einer Zahl: Erklärung und Anwendung
Der Kehrwert einer beliebigen Zahl \(x\) ist diejenige Zahl, die mit \(x\) multipliziert \(1\) ergibt. Die Zahl \(0\) wird dabei ausgeschlossen. In einigen Definitionen oder Aufgaben findest Du eine andere Schreibweise für den Bruch \(\frac{1}{x}\). Du kannst diesen auch als \(x^{-1}\) angeben. Somit gibt es zu jedem Bruch einen „Gegenspieler“, dessen Produkt genau \(1\) ergibt. Der Kehrwert eines Bruches wird als Kehrbruch bezeichnet.
Um den Kehrbruch zu bilden, vertauschst Du den Zähler und den Nenner des angegebenen Bruches: Die Zahl über dem Bruchstrich wird mit der Zahl unter dem Bruchstrich vertauscht. Dadurch erhältst Du den Kehrwert des Bruches.
- \(\frac{{\color{bl}a}}{{\color{gr}b}}\rightarrow\frac{{\color{gr}b}}{{\color{bl}a}}\)
Den Kehrwert einer Potenz berechnest du, indem sich das Vorzeichen des Exponenten ändert. Das bedeutet, dass der Kehrwert von \(a^b\) gleich \(a^{-b}\) ist. Es gilt auch die Rechenregel: \(a^{-b} = \frac{1}{a^b}\).
In der Bruchrechnung benötigst Du den Kehrwert eines Bruchs, um eine Division zweier Brüche durchzuführen. Dazu multiplizierst Du den ersten Bruch mit dem Kehrwert des zweiten Bruchs. Das Produkt von Ausgangsbruch und Kehrwert ergibt immer 1.
Um den Kehrwert einer ganzen Zahl zu bilden, fügst Du der ganzen Zahl einen Nenner der Größe 1 hinzu. Dadurch wird der Wert der Zahl nicht verändert, es handelt sich lediglich um eine andere Schreibweise. Anschließend vertauschst Du Zähler und Nenner, um den Kehrwert der ganzen Zahl zu erhalten.
Wie man den Kehrwert eines Bruchs findet
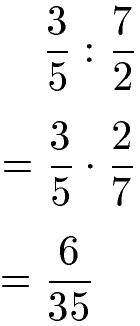
Der Kehrwert einer beliebigen Zahl \(x\) ist diejenige Zahl, die mit \(x\) multipliziert \(1\) ergibt. Die Zahl \(0\) wird dabei ausgeschlossen.
Berechnung des Kehrwerts
Um den Kehrwert eines Bruchs zu bilden, vertauscht man den Zähler und den Nenner des Bruchs. Dadurch erhält man den Kehrwert des Bruchs. Zum Beispiel:
- \(\frac{2}{3}\) – Der Kehrwert ist \(\frac{3}{2}\)
- \(5\) – Um den Kehrwert einer ganzen Zahl zu berechnen, wandelt man sie in eine Bruchzahl um, indem man einen Nenner mit dem Wert 1 hinzufügt. Der Kehrwert von \(5\) ist also \(\frac{1}{5}\).
Kehrbruch und Potenzen
Der Kehrbruch einer Potenz mit Basis \(a\) und Exponenten \(b\) ist gegeben durch \(a^{-b}\). Das bedeutet, dass der Exponent sein Vorzeichen ändert. Zum Beispiel:
- \(5^3 = 125\) – Der Kehrwert ist \(5^{-3} = \frac{1}{125}\)
Anwendung in der Bruchrechnung
In der Bruchrechnung wird der Kehrwert verwendet, um eine Division zweier Brüche durchzuführen. Dabei multipliziert man den ersten Bruch mit dem Kehrwert des zweiten Bruchs.
Der Kehrwert eines Bruchs wird auch als Kehrbruch bezeichnet und ist der „Gegenspieler“ des ursprünglichen Bruchs, dessen Produkt immer \(1\) ergibt.
Ein Kehrwert ist der reziproke Wert einer Zahl, also das Ergebnis, wenn man 1 durch diese Zahl teilt. Er wird verwendet, um Brüche zu vereinfachen und bei mathematischen Berechnungen. Der Kehrwert ist besonders wichtig in den Bereichen Algebra und Arithmetik.

