Ein Funktionsterm ist ein mathematischer Ausdruck, der eine Funktion beschreibt. Er besteht aus Variablen, Konstanten und mathematischen Operationen. Durch Einsetzen von Werten in den Funktionsterm können wir den Funktionswert berechnen. Funktionsterme sind grundlegend für das Verständnis und die Analyse von mathematischen Funktionen.
- Wie alt werden Frösche? Lebenserwartung von Fröschen in Gefangenschaft und Freiland
- Energiepauschale für Rentner: Wann erfolgt Auszahlung in 2023?
- Wie alt dürfen Autoreifen sein? Reifenalter laut TÜV begrenzt.
- Rhabarber ernten: Tipps und Empfehlungen
- Wann entwickelt sich Karpador? So erreichen Sie Garados in Pokémon Karpador Jump
Erklärung: Was ist ein Funktionsterm und wie wird er berechnet?

Ein Funktionsterm ist eine mathematische Vorschrift, die angibt, wie man zu einem bestimmten Wert der unabhängigen Variable den Funktionswert berechnet. Der Funktionsterm wird oft als Gleichung dargestellt, bei der die abhängige Variable auf einer Seite steht und auf der anderen Seite die Rechenvorschrift steht. Zum Beispiel könnte der Funktionsterm einer quadratischen Funktion lauten „-2/3x^2 + 3“. Um den Funktionswert f(x) zu erhalten, muss man also x quadrieren, mit -2/3 multiplizieren und dann 3 addieren.
Die Funktion f(x) = (2-x)e^x ist ein weiteres Beispiel für einen Funktionsterm. Hierbei wird der Funktionswert f(x) berechnet, indem man (2-x) mit e^x multipliziert. Die unabhängige Variable x kann dabei beliebige reelle Werte annehmen.
Es gibt verschiedene Regeln und Techniken, um Funktionsterme zu berechnen. Dazu gehören die Potenzregel, die Produktregel, die Quotientenregel und die Kettenregel. Diese Regeln ermöglichen es uns, komplexe Funktionsterme abzuleiten oder zu vereinfachen.
Der Graph einer Funktion zeigt die Beziehung zwischen der unabhängigen Variable x und dem Funktionswert f(x). Dabei können verschiedene Eigenschaften des Graphen beobachtet werden, wie zum Beispiel waagerechte Asymptoten oder senkrechte Asymptoten. Diese Eigenschaften geben uns Informationen über das Verhalten der Funktion im Unendlichen.
In realen Anwendungen werden Funktionsterme verwendet, um Phänomene oder Prozesse zu modellieren. Zum Beispiel kann die Förderrate eines Ölfeldes über die Zeit mit einer Funktion modelliert werden. In diesem Fall wird die unabhängige Variable t als Maßzahl zur Einheit 1 Jahr interpretiert und der Funktionswert f(t) als Maßzahl zur Einheit 1000 Tonnen pro Jahr.
Ein weiteres Anwendungsbeispiel ist die Modellierung der momentanen Zuflussrate aus einem Bach während eines bestimmten Beobachtungszeitraums. Hier wird die unabhängige Variable t als Maßzahl zur Einheit 1 Stunde interpretiert und der Funktionswert f(t) als Maßzahl zur Einheit 1 Kubikmeter pro Stunde.
In manchen Situationen fließen mehrere Bäche in ein Staubecken oder eine andere Sammelstelle. In solchen Fällen können die momentanen Zuflussraten aus den einzelnen Bächen durch separate Funktionsterme modelliert werden. Die Gesamtzuflussrate aus allen Bächen kann dann durch eine weitere Funktion berechnet werden, indem man die einzelnen Funktionsterme addiert.
Es ist wichtig zu beachten, dass die Lösungsvorschläge für mathematische Probleme nicht in der Verantwortung des Kultusministeriums liegen. Es liegt an jedem Schüler oder jeder Schülerin, diese Aufgaben eigenständig zu lösen und mögliche Lösungen zu erarbeiten.
Definition: Funktionsterm – Die Rechenvorschrift zur Berechnung von Funktionswerten
Ein Funktionsterm ist eine mathematische Formel, nach der man den Wert einer Funktion für einen gegebenen Wert der unabhängigen Variable berechnet. Der Funktionsterm wird auch als „Rechenvorschrift“ bezeichnet.
Der Funktionsterm einer Funktion gibt an, wie man den Funktionswert f(x) berechnet. Zum Beispiel könnte der Funktionsterm einer quadratischen Funktion lauten „-2/3x^2 + 3“. In diesem Fall muss man den Wert x quadrieren, mit -2/3 multiplizieren und dann 3 addieren, um den Funktionswert f(x) zu erhalten.
In der Mathematik wird die Funktionsgleichung oft als „f(x) gleich Funktionsterm“ ausgedrückt. Der Funktionswert f(x) ist das Ergebnis der Anwendung des Funktionsterms auf einen bestimmten Wert der Variablen x.
Es ist wichtig zu beachten, dass der Funktionsterm die grundlegende mathematische Beziehung zwischen der unabhängigen Variable x und dem Funktionswert f(x) darstellt. Er kann verwendet werden, um den Graphen einer Funktion zu zeichnen oder um verschiedene Eigenschaften und Verhaltensweisen der Funktion zu analysieren.
Die Kenntnis des Funktionsterms ermöglicht es uns auch, Ableitungen von Funktionen zu berechnen und ihre Veränderungsrate an verschiedenen Punkten zu bestimmen. Der Ableitungsfunktion hat oft einen eigenen Funktionsterm, der durch Anwendung bestimmter Ableitungsregeln auf den ursprünglichen Funktionsterm erhalten wird.
Der Begriff „Funktionsterm“ ist in vielen mathematischen Bereichen von Bedeutung, einschließlich der Analysis, Algebra und Geometrie. Er spielt eine zentrale Rolle bei der Modellierung und Lösung von mathematischen Problemen in verschiedenen Anwendungsgebieten wie Physik, Wirtschaft und Ingenieurwesen.
Beispiele: Quadratische Funktionen und ihre Funktionsterme
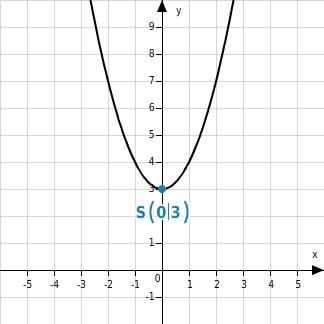
Beispiele: Quadratische Funktionen und ihre Funktionsterme
Quadratische Funktionen sind Funktionen, deren Funktionsterme eine quadratische Gleichung darstellen. Der Funktionsterm einer quadratischen Funktion hat die Form \(ax^2 + bx + c\), wobei \(a\), \(b\) und \(c\) Konstanten sind. Hier sind einige Beispiele für quadratische Funktionen und ihre entsprechenden Funktionsterme:
1. Beispiel: Die quadratische Funktion \(f(x) = x^2 – 3x + 2\) hat den Funktionsterm \(x^2 – 3x + 2\). Um den Funktionswert \(f(x)\) zu berechnen, quadrieren wir den Wert von \(x\), multiplizieren ihn mit \(-3\) und addieren dann \(2\).
2. Beispiel: Die quadratische Funktion \(g(x) = -2x^2 + 5x – 1\) hat den Funktionsterm \(-2x^2 + 5x – 1\). Um den Funktionswert \(g(x)\) zu berechnen, quadrieren wir den Wert von \(x\), multiplizieren ihn mit \(-2\), multiplizieren den Wert von \(x\) mit \(5\) und subtrahieren dann \(1\).
3. Beispiel: Die quadratische Funktion \(h(x) = 4x^2 – x + 7\) hat den Funktionsterm \(4x^2 – x + 7\). Um den Funktionswert \(h(x)\) zu berechnen, quadrieren wir den Wert von \(x\), multiplizieren ihn mit \(4\), multiplizieren den Wert von \(x\) mit \(-1\) und addieren dann \(7\).
Die Funktionsterme geben uns die Rechenvorschrift, nach der wir den Funktionswert einer quadratischen Funktion berechnen können. Indem wir den Wert von \(x\) in den Funktionsterm einsetzen, erhalten wir den entsprechenden Funktionswert.
Anwendung: Modellierung von Ölförder- und Zuflussraten mit Funktionstermen
Die Funktion \(f\) ist gegeben durch \(f(x) = (2-x) \cdot e^x\), \(x \in \mathbb{R}\). Diese Funktion beschreibt die Ölförderrate eines Ölfeldes über einen bestimmten Zeitraum. Der Funktionswert \(f(x)\) gibt dabei die Förderrate in 1000 Tonnen pro Jahr an.
Um den Funktionswert zu berechnen, muss man den Funktionsterm verwenden. In diesem Fall wird der Wert von \(x\) quadriert, dann mit -1 multipliziert und schließlich mit der Exponentialfunktion multipliziert. Das Ergebnis ist die Förderrate.
Die Ableitungsfunktion \(f’\) gibt die momentane Änderungsrate der Förderrate an. Sie kann verwendet werden, um das Verhalten der Förderrate zu analysieren, z.B. ob sie steigt oder fällt.
Ein ähnliches Modell kann auch für die Zuflussrate eines Bachs verwendet werden. Die Funktion \(f(t) = \frac14 t^3 -12t^2 +144t +250\) beschreibt die momentane Zuflussrate in Kubikmetern pro Stunde für einen bestimmten Beobachtungszeitraum. Dabei gibt \(t\) die Zeit in Stunden an.
Für den Fall, dass es zwei Bäche gibt, können separate Funktionen für jeden Bach erstellt werden. Die Gesamtzuflussrate aus beiden Bächen kann dann durch eine weitere Funktion modelliert werden.
Diese Art der Modellierung ermöglicht es uns, das Verhalten von Ölförder- und Zuflussraten über einen bestimmten Zeitraum zu analysieren und Vorhersagen darüber zu treffen. Es ist ein nützliches Werkzeug in der Wissenschaft und der Industrie, um Entscheidungen zu treffen und Prozesse zu optimieren.
Ableitungsfunktionen: Zusammenhang zwischen Funktionsterm und Ableitungsfunktion
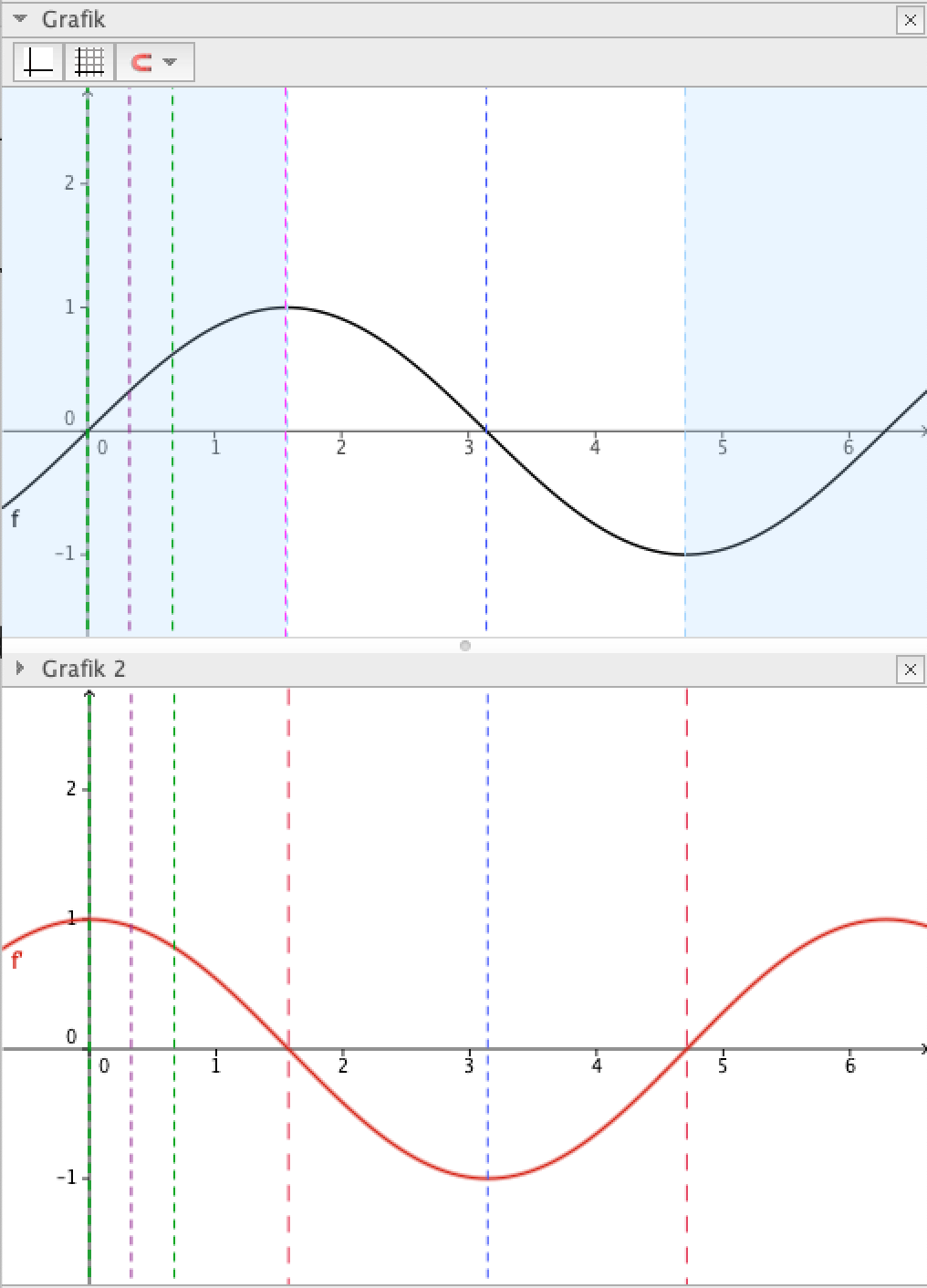
Die Ableitungsfunktion gibt uns Informationen über die Steigung der Funktion an jedem Punkt ihres Graphen. Sie ist definiert als die Ableitung der Funktion, also die Rate, mit der sich der Funktionswert ändert, wenn sich der Wert der unabhängigen Variable leicht verändert.
Um die Ableitungsfunktion zu berechnen, verwenden wir Ableitungsregeln wie die Potenzregel, Produktregel oder Quotientenregel. Diese Regeln ermöglichen es uns, den Funktionsterm in einen Ausdruck umzuwandeln, der den Funktionswert der Ableitungsfunktion angibt.
Der Zusammenhang zwischen dem Funktionsterm und dem Ausdruck für die Ableitungsfunktion kann durch verschiedene Regeln beschrieben werden:
– Konstantenregel: Die Ableitung einer konstanten Funktion ist immer null.
– Faktorregel: Die Ableitung einer Funktion multipliziert mit einer Konstante ist gleich dieser Konstante mal der Ableitung der Funktion.
– Summenregel: Die Ableitung einer Summe von zwei Funktionen ist gleich der Summe ihrer jeweiligen Ableitungen.
– Kettenregel: Die Ableitung einer zusammengesetzten Funktion besteht aus dem Produkt der Ableitungen ihrer inneren und äußeren Funktionen.
– Nullstellen: Eine Nullstelle des Funktionsterms entspricht einem Extremum (Minimum oder Maximum) des Funktionsgraphen.
Zusätzlich zu diesen Regeln können wir auch das Verhalten des Funktionsgraphen im Unendlichen analysieren. Wir untersuchen dabei mögliche waagerechte Asymptoten (wenn sich die Funktionswerte bestimmten Grenzwerten annähern), senkrechte Asymptoten (wenn die Funktion an bestimmten Punkten nicht definiert ist) und schräge Asymptoten (wenn sich der Funktionsgraph einer Geraden annähert).
Insgesamt ermöglichen uns die Ableitungsfunktionen, wichtige Informationen über den Funktionsverlauf zu gewinnen und ermöglichen es uns, den Funktionsterm in Bezug auf seine Steigung zu analysieren.
Funktionsterm in der Praxis: Modellierung von Bachzuflüssen mit Funktionstermen

Der Funktionsterm ist ein mathematischer Ausdruck, der verwendet wird, um den Funktionswert einer Funktion zu berechnen. Er gibt die „Rechenvorschrift“ an, nach der man zu einem gegebenen Wert der unabhängigen Variable den Wert der Funktion erhält.
In der Praxis werden Funktionsterme häufig verwendet, um reale Phänomene oder Prozesse zu modellieren. Ein Beispiel dafür ist die Modellierung von Bachzuflüssen. Hierbei kann die momentane Zuflussrate aus einem Bach durch eine Funktion mit einem bestimmten Funktionsterm beschrieben werden.
Um den Funktionsterm aufzustellen, müssen zunächst die gegebenen Informationen berücksichtigt werden, wie z.B. die Einheit der unabhängigen und abhängigen Variablen sowie der Beobachtungszeitraum. Anhand dieser Informationen kann dann ein geeigneter Ausdruck für den Funktionsterm erstellt werden.
Es ist wichtig zu beachten, dass verschiedene Faktoren bei der Modellierung berücksichtigt werden können, wie z.B. Regenfälle unterschiedlicher Dauer und Stärke oder das Zusammenfließen mehrerer Bäche. In solchen Fällen können mehrere Funktionsterme verwendet werden, um die einzelnen Zuflussraten zu modellieren und schließlich einen Gesamt-Funktionsterm für die Gesamtzuflussrate zu erhalten.
Die Verwendung von Funktionstermen ermöglicht es uns, komplexe Phänomene zu analysieren und Vorhersagen über ihr Verhalten zu treffen. Sie sind daher ein wichtiges Werkzeug in verschiedenen Bereichen wie Physik, Biologie oder Wirtschaft.
Zusammenfassend lässt sich sagen, dass der Funktionsterm eine mathematische Rechenvorschrift ist, die verwendet wird, um den Funktionswert einer Funktion zu berechnen. In der Praxis werden Funktionsterme häufig verwendet, um reale Phänomene oder Prozesse zu modellieren und ihr Verhalten zu analysieren.
Ein Funktionsterm ist ein mathematischer Ausdruck, der eine Funktion beschreibt. Er enthält Variablen und Konstanten, die durch mathematische Operationen miteinander verknüpft sind. Durch Einsetzen von Werten in den Funktionsterm können wir den Funktionswert berechnen. Funktionsterme spielen eine wichtige Rolle in der Analysis und ermöglichen es uns, komplexe mathematische Zusammenhänge darzustellen und zu analysieren.

