Was ist ein Flächeninhalt? Alles, was du wissen musst.

Der Flächeninhalt ist ein mathematischer Begriff, der die Größe einer Fläche beschreibt. Er gibt an, wie viel Raum eine Figur auf einer Ebene einnimmt. Der Flächeninhalt wird durch das Ausmessen und Berechnen der Länge und Breite bestimmt. In diesem Artikel erfährst du, was genau der Flächeninhalt ist und wie er berechnet wird.

Was ist ein Flächeninhalt und wie wird er berechnet?

Der Flächeninhalt ist ein Maß für die Größe eines zweidimensionalen Objekts oder einer Figur. Er gibt an, wie viel Fläche das Objekt einnimmt. Der Flächeninhalt wird oft auch einfach als „Fläche“ bezeichnet, was jedoch missverständlich sein kann, da dieser Begriff sowohl das Objekt selbst als auch seine Größe umfassen kann.

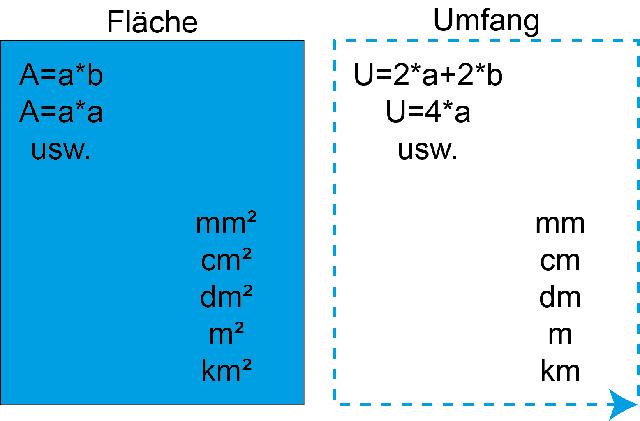
Die Basiseinheit des Flächeninhalts ist der Quadratmeter (m²). Man kann jedoch jede andere Längeneinheit quadrieren, um eine Flächeneinheit zu erhalten. Zum Beispiel sind 100 Meter mal 100 Meter ein Hektar und (1 cm)² sind ein Quadratzentimeter.

Für viele Figuren gibt es einfache Formeln zur Berechnung des Flächeninhalts. So ist zum Beispiel die Fläche eines Rechtecks das Produkt seiner beiden benachbarten Seitenlängen. Wenn eine Figur von einer beliebig geformten Kurve begrenzt wird, die der Graph einer Funktion ist, kann man den Flächeninhalt mithilfe der Integralrechnung berechnen.

Der Flächeninhalt einer zusammengesetzten Figur ergibt sich aus der Summe der Einzelflächen. Die Analytische Geometrie bietet weitere Möglichkeiten zur Bestimmung von Flächeninhalten. Zum Beispiel ist die Fläche eines Parallelogramms der Betrag des Kreuzprodukts der beiden Vektoren, die es aufspannen.

Insgesamt dient der Flächeninhalt dazu, die Größe und Ausdehnung von zweidimensionalen Objekten zu quantifizieren und zu vergleichen.

Die Bedeutung des Flächeninhalts für geometrische Figuren

Achsensymmetrie

Achsensymmetrie ist eine Eigenschaft von geometrischen Figuren, bei der die Figur durch eine Achse in zwei spiegelbildliche Hälften geteilt werden kann. Diese Achse wird als Spiegelachse bezeichnet. Jeder Punkt auf der einen Seite der Spiegelachse hat ein entsprechendes spiegelbildliches Pendant auf der anderen Seite. Die Figur bleibt unverändert, wenn sie entlang der Spiegelachse gespiegelt wird. Ein Punkt, der sich auf der Spiegelachse befindet, wird als Spiegelpunkt bezeichnet. Eine Figur wird als achsensymmetrisch oder spiegelsymmetrisch bezeichnet, wenn sie mindestens eine Spiegelachse besitzt.

Beispiele für achsensymmetrische Figuren sind das Quadrat und das Rechteck. Die Diagonale einer solchen Figur ist oft eine Spiegelachse. Wenn man diese Figuren entlang ihrer Spiegelachsen spiegelt, bleiben sie unverändert.

Ähnlichkeit

Ähnlichkeit ist ein Begriff aus der Geometrie, der beschreibt, dass zwei Figuren trotz unterschiedlicher Größe und Proportionen die gleiche Form haben. Zwei Figuren sind ähnlich zueinander, wenn ihre entsprechenden Seiten proportional zueinander sind und ihre entsprechenden Winkel gleich groß sind.

Eine Ähnlichkeitsabbildung ist eine Transformation, die eine Figur in eine ähnliche Figur überführt. Dabei bleiben die Winkel zwischen den Seiten erhalten und die Seitenverhältnisse werden beibehalten. Eine Figur kann durch eine Ähnlichkeitsabbildung vergrößert oder verkleinert werden, aber ihre Form bleibt erhalten.

Die Ähnlichkeit von Figuren ermöglicht es uns, Proportionen und Verhältnisse zu analysieren und zu vergleichen. Sie ist auch in vielen Anwendungen der Geometrie von Bedeutung, wie zum Beispiel bei der Konstruktion von Karten oder Modellen.

Beispiele für ähnliche Figuren sind zwei Dreiecke, bei denen die Winkel gleich groß sind und die Seitenlängen proportional zueinander stehen.

Verschiedene Methoden zur Berechnung des Flächeninhalts

1. Formeln für einfache Figuren

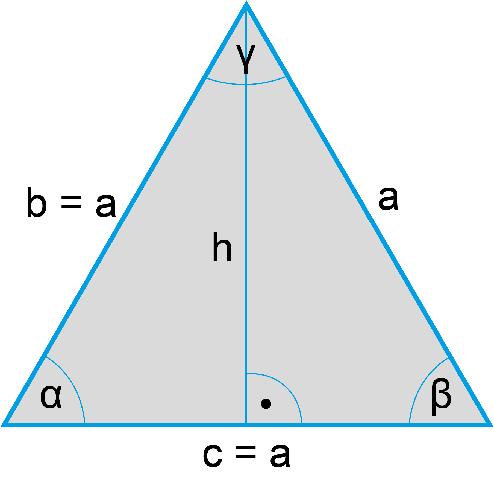
Für viele geometrische Figuren gibt es einfache Formeln zur Berechnung des Flächeninhalts. Zum Beispiel ist die Fläche eines Rechtecks das Produkt seiner beiden benachbarten Seitenlängen. Für ein Dreieck kann man die Fläche mit der Formel „Grundseite mal Höhe geteilt durch 2“ berechnen. Andere Beispiele sind die Formeln für den Flächeninhalt eines Quadrats, Kreises oder Trapezes.

2. Integralrechnung

Wenn eine Figur von einer beliebig geformten Kurve begrenzt wird, die der Graph einer Funktion ist, kann man ihren Flächeninhalt mithilfe der Integralrechnung berechnen. Dabei wird das Integral über die Funktion gebildet und liefert den Flächeninhalt unterhalb der Kurve.

3. Zusammengesetzte Figuren

Der Flächeninhalt einer zusammengesetzten Figur ist die Summe der Einzelflächen, aus denen sie besteht. Man zerlegt die Figur in einfachere Teilfiguren und berechnet jeweils den Flächeninhalt dieser Teile. Anschließend werden alle Teilflächen addiert, um den Gesamtflächeninhalt zu erhalten.

4. Analytische Geometrie

Die analytische Geometrie bietet weitere Möglichkeiten zur Bestimmung von Flächeninhalten. Zum Beispiel kann man den Flächeninhalt eines Parallelogramms mit dem Betrag des Kreuzprodukts der beiden Vektoren berechnen, die es aufspannen. Für das Volumen eines Parallelepipeds verwendet man das Betrag des Spatprodukts der drei es aufspannenden Vektoren. Diese Methoden sind besonders nützlich, wenn die Figuren nicht geometrisch einfach zu berechnen sind.

Analytische Geometrie: Bestimmung von Flächeninhalten

Die Analytische Geometrie bietet verschiedene Methoden zur Bestimmung von Flächeninhalten. Eine Möglichkeit besteht darin, den Flächeninhalt einer Figur als Betrag des Kreuzprodukts der beiden Vektoren zu berechnen, die sie aufspannen. Zum Beispiel ist der Flächeninhalt eines Parallelogramms gegeben durch \(A_\text{Parallelogramm} = \left| \vec a \times \vec b \right|\), wobei \(\vec a\) und \(\vec b\) die beiden Vektoren sind, die das Parallelogramm aufspannen.

Eine weitere Methode zur Berechnung von Flächeninhalten ist das Spatprodukt der drei Vektoren, die ein Parallelepipeds aufspannen. Das Volumen des Parallelepipeds entspricht dem Betrag des Spatprodukts dieser drei Vektoren: \(V_\text{Parallelepiped} = \left| \left( \vec a \times \vec b \right) \cdot \vec c \right|\).

Es ist wichtig zu beachten, dass diese Methoden nur für geometrische Objekte im dreidimensionalen Raum gelten. Für zweidimensionale Figuren gibt es andere Formeln und Berechnungsmethoden, wie zum Beispiel das Produkt der Seitenlängen für Rechtecke.

Zusätzlich zur Analytischen Geometrie gibt es auch andere mathematische Ansätze zur Bestimmung von Flächeninhalten, wie zum Beispiel die Integralrechnung. Wenn eine Figur von einer beliebig geformten Kurve begrenzt wird, kann ihr Flächeninhalt mithilfe von Integralen berechnet werden.

Insgesamt bietet die Analytische Geometrie eine Vielzahl von Möglichkeiten zur Bestimmung von Flächeninhalten, abhängig von der Art der Figur und den gegebenen Informationen. Es ist wichtig, die jeweiligen Formeln und Methoden entsprechend anzuwenden, um genaue Ergebnisse zu erzielen.

Achsensymmetrie: Eine wichtige Eigenschaft von Figuren

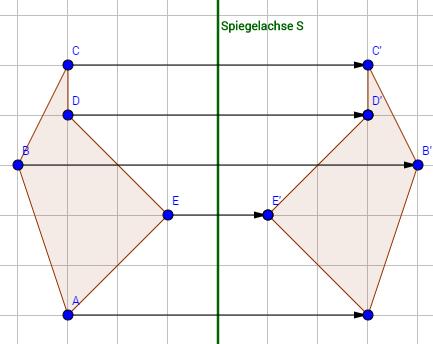
Die Achsensymmetrie ist eine wichtige Eigenschaft von Figuren in der Geometrie. Eine Figur wird als achsensymmetrisch bezeichnet, wenn sie durch eine Achse in zwei spiegelbildliche Hälften geteilt werden kann. Diese Achse wird auch als Spiegelachse bezeichnet.

Die Achsensymmetrie kann anhand verschiedener Merkmale erkannt werden. Zum einen sind die beiden Hälften der Figur spiegelbildlich zueinander angeordnet, das heißt, sie sind exakt gleich, nur gespiegelt. Zum anderen gibt es einen Punkt auf der Spiegelachse, den man als Spiegelpunkt bezeichnet. Dieser Punkt bleibt bei einer Spiegelung unverändert.

Eine Figur kann sowohl punktsymmetrisch als auch spiegelsymmetrisch sein. Bei einer punktsymmetrischen Figur gibt es einen Punkt im Zentrum, um den die Figur gedreht werden kann und trotzdem bleibt sie unverändert. Bei einer spiegelsymmetrischen Figur hingegen gibt es keine spezielle Drehachse, sondern nur eine Spiegelachse.

Die Achsensymmetrie ist eine äußerst nützliche Eigenschaft von Figuren. Sie ermöglicht es uns, bestimmte Eigenschaften oder Bereiche einer Figur zu bestimmen, indem wir uns nur auf eine Hälfte der Figur konzentrieren und dann diese Informationen auf die andere Hälfte übertragen.

Insgesamt ist die Achsensymmetrie ein wichtiges Konzept in der Geometrie und findet in vielen Bereichen Anwendung, wie zum Beispiel bei der Konstruktion von Gebäuden, der Gestaltung von Kunstwerken oder auch in der Natur, wo viele Organismen achsensymmetrisch aufgebaut sind.

Ähnlichkeit von Figuren: Was bedeutet das genau?

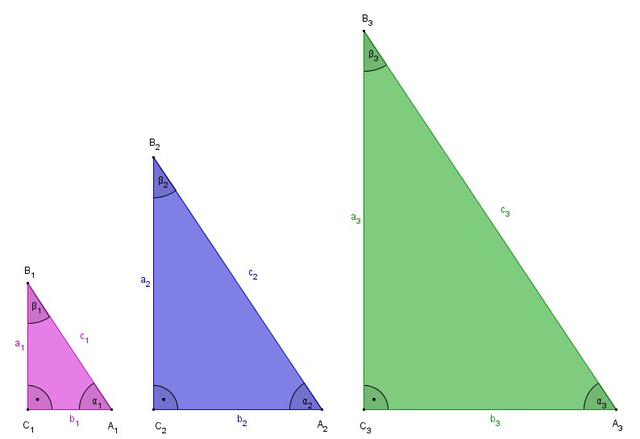
Ähnlichkeit von Figuren bedeutet, dass zwei oder mehrere Figuren die gleiche Form haben, jedoch unterschiedliche Größen aufweisen können. Bei ähnlichen Figuren sind alle Winkel gleich groß und die entsprechenden Seitenverhältnisse sind proportional zueinander.

Eine Ähnlichkeitsabbildung ist eine Transformation, bei der eine Figur in eine ähnliche Figur überführt wird. Dabei bleiben die Winkel erhalten und die Seiten werden entsprechend gestreckt oder gestaucht.

Ähnlichkeit ist ein wichtiges Konzept in der Geometrie, da es ermöglicht, Beziehungen zwischen verschiedenen Figuren herzustellen und Eigenschaften abzuleiten. Zum Beispiel können wir mithilfe von Ähnlichkeit den Flächeninhalt einer Figur berechnen, indem wir das Verhältnis der Seitenlängen quadrieren.

Es gibt verschiedene Möglichkeiten, Ähnlichkeit zu erkennen. Eine Möglichkeit besteht darin, die Längenverhältnisse der Seiten zu vergleichen. Wenn diese Verhältnisse gleich sind, handelt es sich um ähnliche Figuren.

Ähnlichkeit spielt auch eine Rolle in der Modellierung und Skalierung von Objekten. Zum Beispiel werden Landkarten oft im Verhältnis zur tatsächlichen Größe verkleinert dargestellt, um einen Überblick über große Gebiete zu ermöglichen.

Insgesamt ermöglicht uns das Konzept der Ähnlichkeit von Figuren, geometrische Beziehungen zu verstehen und mathematische Modelle für reale Situationen zu entwickeln.

Der Flächeninhalt ist eine wichtige Größe, um die Ausdehnung einer Fläche zu bestimmen. Er wird berechnet, indem die Länge und Breite multipliziert werden. Der Flächeninhalt ermöglicht es uns, verschiedene Objekte zu vergleichen und ihre Größe zu bestimmen. Es ist ein grundlegendes Konzept in der Mathematik und findet Anwendung in vielen Bereichen wie Geometrie und Physik. Die Kenntnis des Flächeninhalts ist daher von großer Bedeutung für das Verständnis unserer Umgebung.