Der Funktionswert ist ein zentraler Begriff in der Mathematik. Er beschreibt den Wert, den eine Funktion für einen bestimmten Eingabewert annimmt. In diesem Artikel erfährst du, was der Funktionswert genau ist und wie er berechnet wird.
- Entdecke, was sich auf ‚Welt‘ reimt – Die Bedeutung der Kräuter und Hempf für unsere Gesundheit!
- Selbstgemachter Baileys Likör – Ein leckerer Genuss
- Bauanleitung für einen DIY Wasserfilter – So einfach geht es!
- Verwendungsideen für Quitten: Leckere Rezepte für Quittengelee, Sirup und mehr!
- Lippenstift selber machen – So kreierst du deinen eigenen individuellen Look
Was ist der Funktionswert und wie berechnet man ihn?
Ein Funktionswert ist der Wert auf der y-Achse, der zu einem bestimmten x-Wert einer Funktion gehört. Der Funktionswert wird verwendet, um den Punkt auf dem Graphen einer Funktion zu bestimmen. Es gibt zwei Möglichkeiten, den Funktionswert zu bestimmen: grafisch oder durch Einsetzen in den Funktionsterm.
Um den Funktionswert grafisch zu bestimmen, kann man in drei Schritten vorgehen:
1. Man geht entlang der x-Achse bis zum gegebenen x-Wert.
2. Von diesem Punkt aus wandert man nach links oder rechts bis zur y-Achse.
3. Dort liest man den Wert ab, das ist dann der Funktionswert.
Beim Einsetzen in den Funktionsterm muss man den gegebenen x-Wert in die Funktion einsetzen und das Ergebnis berechnen. Zum Beispiel, um den Funktionswert für den Term f(x) = 2x + 3 an der Stelle x = 4 zu berechnen, setzt man die 4 für x in die Funktionsgleichung ein und erhält f(4) = 2*4 + 3 = 11.
Der Definitionsbereich einer Funktion umfasst alle Zahlen, die als x-Werte in die Funktion eingesetzt werden können. Der Wertebereich hingegen sind alle möglichen y-Werte, die bei dem Einsetzen herauskommen können.
Zusammenfassend kann gesagt werden, dass der Funktionswert der zugehörige Wert auf der y-Achse zu einem bestimmten x-Wert auf der x-Achse ist. Man kann ihn entweder grafisch bestimmen oder durch Einsetzen in den Funktionsterm berechnen.
Der Funktionswert: Definition und Berechnung einfach erklärt
Was ist der Funktionswert?
Der Funktionswert ist der zugehörige Wert auf der y-Achse zu einer bestimmten Stelle auf der x-Achse. Jeder x-Wert in einer Funktion hat einen eindeutigen Funktionswert, der den Punkt auf dem Graphen bestimmt.
Wie berechnet man den Funktionswert?
Es gibt zwei Möglichkeiten, den Funktionswert zu berechnen: grafisch oder durch Einsetzen in den Funktionsterm. Beim grafischen Bestimmen des Funktionswerts geht man in drei Schritten vor: Man findet die entsprechende Stelle auf der x-Achse, wandert von dort aus nach links oder rechts bis zur y-Achse und liest den Wert ab. Dieser abgelesene Wert ist dann der Funktionswert.
Alternativ kann man den Funktionswert auch durch Einsetzen des x-Werts in den Funktionsterm berechnen. Dazu setzt man den gegebenen x-Wert in die Funktion ein und rechnet das Ergebnis aus. Das Ergebnis ist dann der zugehörige y-Wert bzw. der Funktionswert.
Beispiel:
Um den Funktionswert für x = 4 bei der Funktion f(x) = 2x + 3 zu berechnen, setzt man den Wert 4 für x in die Funktion ein:
f(4) = 2 * 4 + 3
f(4) = 8 + 3
f(4) = 11
Der zugehörige y-Wert bzw. Funktionswert ist also 11.
Funktionswerte verstehen und berechnen: Eine Anleitung
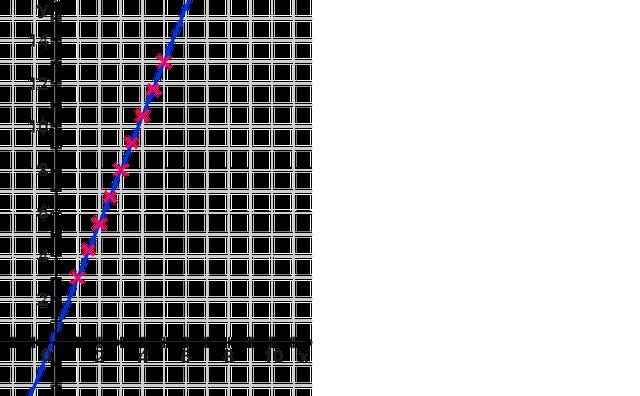
Was ist der Funktionswert?
Der Funktionswert ist der zugehörige Wert auf der y-Achse zu einer bestimmten Stelle auf der x-Achse. Bei einer Funktion gehört zu jedem x-Wert ein Wert auf der y-Achse. Diese beiden Werte bilden dann zusammen einen Punkt auf dem Graphen.
Wie kann man den Funktionswert grafisch bestimmen?
Um den Funktionswert grafisch zu bestimmen, kannst du folgende Schritte befolgen:
1. Gehe entlang der x-Achse bis zum gegebenen x-Wert.
2. Markiere dir diese Stelle.
3. Von diesem Punkt aus wanderst du nach links oder rechts bis zur y-Achse und liest den Wert ab. Dieser abgelesene Wert ist dein Funktionswert.
Tipp: Beim grafischen Bestimmen von Funktionswerten können oft keine exakten Werte abgelesen werden. Deshalb ist es immer genauer, den Funktionswert zusätzlich noch einmal durch Einsetzen in den Funktionsterm zu berechnen.
Wie berechnet man den Funktionswert?
Um den Funktionswert zu berechnen, setzt du den gegebenen x-Wert in den Funktionsterm ein und rechnest das Ergebnis aus.
Beispiel:
Gegeben ist die Funktion f(x) = 2x + 4 und wir möchten den Funktionswert für x = 3 berechnen.
Dazu setzen wir die 3 für x in die Funktion ein:
f(3) = 2 * 3 + 4
f(3) = 6 + 4
f(3) = 10
Das Ergebnis für den Funktionswert ist also 10.
Definitionsbereich und Wertebereich
Der Definitionsbereich umfasst alle Zahlen, die du als x in eine Funktion einsetzen kannst. Der Wertebereich hingegen bezeichnet alle möglichen y-Werte, die bei dem Einsetzen von x herauskommen können.
Super! Jetzt weißt du, wie man Funktionswerte versteht und berechnet. Wenn du mehr darüber erfahren möchtest, wie man das bei einer linearen Funktion anwendet, schau dir unser Video dazu an!
Alles, was du über den Funktionswert wissen musst
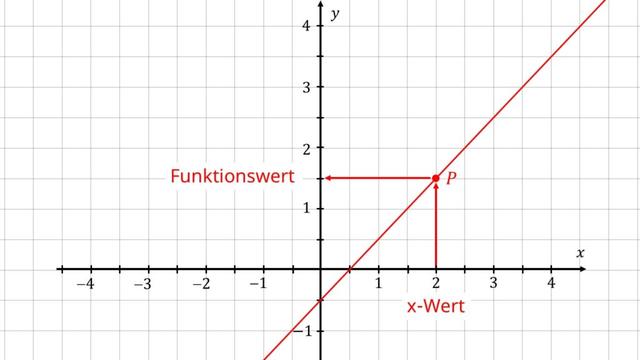
Was ist der Funktionswert?
Der Funktionswert ist der zugehörige Wert auf der y-Achse zu einer bestimmten Stelle auf der x-Achse. Bei einer Funktion bildet jeder x-Wert zusammen mit seinem Funktionswert einen Punkt auf dem Graphen.
Wie kann man den Funktionswert bestimmen?
Es gibt zwei Möglichkeiten, den Funktionswert zu bestimmen: grafisch oder durch Berechnung. Grafisch kannst du den Wert ablesen, indem du entlang der x-Achse zum entsprechenden x-Wert gehst und dann nach links oder rechts bis zur y-Achse wanderst. Der abgelesene Wert ist dein Funktionswert. Alternativ kannst du auch den x-Wert in den Funktionsterm einsetzen und das Ergebnis berechnen.
Beispiel zur Berechnung des Funktionswerts:
Angenommen, wir haben die Funktion f(x) = 2x + 4 und möchten den Funktionswert für x = 3 berechnen. Wir setzen also den Wert 3 für x in die Funktion ein und rechnen: f(3) = 2 · 3 + 4 = 10. Der zugehörige y-Wert zum x-Wert 3 beträgt also 10.
Durch diese Vorgehensweise kannst du den Funktionswert für beliebige x-Werte berechnen und somit Punkte auf dem Graphen einer Funktion bestimmen.
Wie finde ich den Funktionswert? Tipps und Tricks
Grafische Bestimmung des Funktionswerts:
– Gehe auf der x-Achse entlang bis zum gegebenen x-Wert und markiere dir die Stelle.
– Von diesem Punkt aus wandere nach links oder rechts bis zur y-Achse und lese den Wert ab.
– Dieser abgelesene Wert ist der Funktionswert.
Berechnung des Funktionswerts:
– Setze den gegebenen x-Wert in den Funktionsterm ein.
– Berechne das Ergebnis, indem du den Funktionsterm mit dem eingesetzten x-Wert ausrechnest.
– Das Ergebnis ist der Funktionswert.
Beispiel:
Gegeben ist die Funktion f(x) = 2x + 4. Um den Funktionswert für x = 3 zu berechnen, setzt du den Wert 3 in die Funktion ein: f(3) = 2 · 3 + 4. Durch Ausrechnen erhältst du den zugehörigen y-Wert f(3) = 10.
Es ist wichtig zu beachten, dass der x-Wert und der zugehörige y-Wert immer zusammengehören und einen Punkt auf dem Graphen bilden. Der Definitionsbereich umfasst alle möglichen Werte, die für x in die Funktion eingesetzt werden können. Die Menge aller möglichen y-Werte, die dabei herauskommen können, bildet den Wertebereich.
Die grafische Bestimmung des Funktionswerts kann manchmal ungenaue Werte liefern, daher ist es empfehlenswert, den Funktionswert zusätzlich durch Berechnung zu bestimmen.
Funktionswert bestimmen: Grafisch oder durch Einsetzen berechnen
Um den Funktionswert einer Funktion zu bestimmen, gibt es zwei Möglichkeiten: grafisch oder durch Einsetzen in den Funktionsterm.
Grafische Bestimmung des Funktionswerts
Bei der grafischen Bestimmung gehst du auf der x-Achse entlang bis zum entsprechenden x-Wert und markierst dir die Stelle. Von diesem Punkt aus wanderst du nach links oder rechts bis zur y-Achse und liest den Wert ab. Dieser abgelesene Wert ist der Funktionswert.
Berechnung des Funktionswerts durch Einsetzen
Um den Funktionswert durch Einsetzen in den Funktionsterm zu berechnen, setzt du den gegebenen x-Wert in die Funktion ein und rechnest das Ergebnis aus. Das Ergebnis ist dann der zugehörige y-Wert bzw. Funktionswert.
Beispiel: Du sollst den Funktionswert für den Term f(x) = 2x + 4 an der Stelle x = 3 berechnen. Du setzt also die 3 für x in die Funktion ein: f(3) = 2 * 3 + 4. Das Ergebnis dieser Rechnung ist f(3) = 10, also ist der Funktionswert bei x = 3 gleich 10.
Durch grafische Bestimmung oder Berechnung kannst du den Funktionswert einer Funktion ermitteln und somit einen Punkt auf dem Graphen darstellen.
Der Funktionswert ist der Wert, den eine Funktion für einen bestimmten Eingabewert annimmt. Er gibt an, welchen Wert die Funktion für eine gegebene Variable oder Kombination von Variablen zurückgibt. Der Funktionswert ist daher ein zentraler Begriff in der Mathematik und wird verwendet, um Beziehungen zwischen Variablen zu beschreiben und zu analysieren.