Regeln für Plus und Minus: Was ergibt Plus und Minus?

Die Addition und Subtraktion sind grundlegende mathematische Operationen, die uns helfen, Zahlen zu verbinden oder voneinander abzuziehen. In diesem Artikel werden wir uns mit der Frage beschäftigen: „Was ergibt Plus und Minus?“ Wir werden die Regeln und Eigenschaften dieser beiden Operationen untersuchen und ihre Anwendungen in verschiedenen Bereichen kennenlernen. Lassen Sie uns gemeinsam herausfinden, wie Plus und Minus funktionieren!

Vorzeichenregeln: Was ergibt Plus und Minus?

Vorzeichenregeln sind Rechenregeln, die bei der Addition und Multiplikation von Zahlen mit Vorzeichen beachtet werden müssen. Sie gelten für ganze, rationale und reelle Zahlen, jedoch nicht für natürliche und Bruchzahlen.

Das negative Vorzeichen „–“ wandelt eine Zahl in ihre Gegenzahl um. Das bedeutet, dass aus einer positiven Zahl eine negative wird (a → -a) und aus einer negativen Zahl eine positive (-a → -(-a) = +a). Das positive Vorzeichen „+“ verändert eine Zahl nicht. Es wird oft weggelassen oder nur dann aufgeführt, wenn verdeutlicht werden soll, dass es sich um keine negative Zahl handelt.

Bei der Multiplikation gelten folgende Vorzeichenrechenregeln:

– Wenn man zwei Faktoren mit gleichen Vorzeichen multipliziert, erhält man ein positives Produkt. Die Merkregel lautet: „Plus mal Plus ergibt Plus.“ (+5) · (+5) = +25 = 25
– Wenn man zwei Faktoren mit unterschiedlichen Vorzeichen multipliziert, erhält man ein negatives Produkt. Die Merkregel lautet: „Plus mal Minus ergibt Minus.“ (+5) · (-5) = -25

Ein Produkt aus n Faktoren ist positiv, wenn es eine gerade Anzahl an negativen Faktoren enthält (0 gilt als gerade). Ein Produkt aus n Faktoren ist negativ, wenn es eine ungerade Anzahl an negativen Faktoren enthält.

Diese Regeln gelten auch für Quotienten (sofern der Nenner nicht 0 ist), da jede Division als Multiplikation mit dem Kehrwert des Divisors geschrieben werden kann.

Äquivalent bedeutet, dass zwei Terme oder Ausdrücke denselben Wert haben. Man kann sie also gegenseitig ersetzen, ohne den Wert des Ausdrucks zu verändern. Äquivalente Umformungen sind Schritte, bei denen ein Term in einen äquivalenten umgeformt wird. Dabei können verschiedene Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division angewendet werden.

Ausklammern ist eine Methode zur Vereinfachung von Termen. Dabei werden gemeinsame Faktoren aus einem Term herausgezogen und vor die Klammer geschrieben. Dies ermöglicht es, den Term zu vereinfachen und übersichtlicher zu gestalten. Beim Ausklammern können auch Minuswerte aus einer Klammer herausgenommen werden.

Der größte gemeinsame Teiler (ggT) oder größte gemeinsame Faktor (ggt) zweier Zahlen ist die größte Zahl, durch die beide Zahlen ohne Rest teilbar sind. Beim Ausklammern sucht man nach dem größten gemeinsamen Teiler der einzelnen Terme und zieht ihn vor die Klammer.

Diese Vorzeichenregeln und das Ausklammern sind wichtige Konzepte beim Rechnen mit Zahlen und helfen dabei, mathematische Ausdrücke zu vereinfachen und richtig zu interpretieren.

Rechenregeln für Vorzeichen: Plus und Minus

Die Vorzeichenregeln sind Rechenregeln, die bei der Addition und Subtraktion von Zahlen mit Vorzeichen beachtet werden müssen. Es gibt zwei Vorzeichen: das positive Vorzeichen „+“ und das negative Vorzeichen „-„.

Das positive Vorzeichen verändert eine Zahl nicht und wird oft weggelassen, wenn es keine negativen Zahlen gibt. Das negative Vorzeichen wandelt eine positive Zahl in ihre Gegenzahl um und macht aus einer negativen Zahl eine positive Zahl.

Bei der Multiplikation gelten folgende Regeln: Wenn man zwei Faktoren mit dem gleichen Vorzeichen multipliziert, erhält man ein positives Produkt. Zum Beispiel ergibt (+5) · (+5) = +25. Wenn man zwei Faktoren mit unterschiedlichen Vorzeichen multipliziert, erhält man ein negatives Produkt. Zum Beispiel ergibt (+5) · (-5) = -25.

Diese Regeln gelten auch für Divisionen, solange der Nenner nicht Null ist.

Ein Term kann durch Ausklammern vereinfacht werden. Dabei sucht man den größten gemeinsamen Faktor aller Terme und zieht ihn vor die Klammer. Dadurch können Minuswerte aus den Termen entfernt werden.

Äquivalent bedeutet, dass zwei Terme oder Gleichungen den gleichen Wert haben oder die gleiche Bedeutung haben. Man kann einen Term umformen oder umstellen, indem man äquivalente Umformungen anwendet. Diese Umformungen sind gleichwertig und führen zum gleichen Ergebnis.

Zusammenfassend sind die Rechenregeln für Plus und Minus wichtige Regeln beim Rechnen mit Zahlen mit Vorzeichen. Sie müssen beim Rechnen mit ganzen, rationalen und reellen Zahlen berücksichtigt werden. Durch Ausklammern kann ein Term vereinfacht werden und äquivalente Umformungen führen zu gleichen Ergebnissen.

Bedeutung von Plus und Minus in der Mathematik

Die Symbole „+“ und „-“ haben in der Mathematik eine wichtige Bedeutung. Sie dienen dazu, positive und negative Zahlen zu kennzeichnen und mathematische Operationen wie Addition, Subtraktion, Multiplikation und Division zu definieren.

Das positive Vorzeichen „+“ wird verwendet, um positive Zahlen darzustellen. Es zeigt an, dass eine Zahl größer als Null ist. Zum Beispiel ist „+5“ eine positive Zahl, die größer als Null ist.

Das negative Vorzeichen „-“ wird verwendet, um negative Zahlen darzustellen. Es zeigt an, dass eine Zahl kleiner als Null ist. Zum Beispiel ist „-5“ eine negative Zahl, die kleiner als Null ist.

Bei der Addition werden die Vorzeichen der beiden addierten Zahlen berücksichtigt. Wenn beide Zahlen das gleiche Vorzeichen haben (entweder beide positiv oder beide negativ), wird das Ergebnis positiv sein. Wenn die beiden Zahlen unterschiedliche Vorzeichen haben (eine positiv und eine negativ), wird das Ergebnis negativ sein.

Bei der Subtraktion kann man das Minuszeichen verwenden, um den Unterschied zwischen zwei Zahlen auszudrücken. Zum Beispiel ergibt die Subtraktion von 8 minus 3 das Ergebnis 5 (-8 – (-3) = -8 + 3 = -5).

In der Multiplikation gibt es auch Regeln für die Vorzeichen. Wenn man zwei Faktoren mit dem gleichen Vorzeichen multipliziert (entweder beide positiv oder beide negativ), wird das Produkt positiv sein. Wenn man jedoch zwei Faktoren mit unterschiedlichen Vorzeichen multipliziert (eine positiv und eine negativ), wird das Produkt negativ sein.

Diese Regeln für die Vorzeichen sind wichtig, um korrekte mathematische Berechnungen durchzuführen und das richtige Vorzeichen für das Ergebnis zu bestimmen. Sie werden in verschiedenen mathematischen Bereichen wie Algebra, Geometrie und Analysis angewendet.

Multiplikation mit Vorzeichen: Ergebnis von Plus und Minus

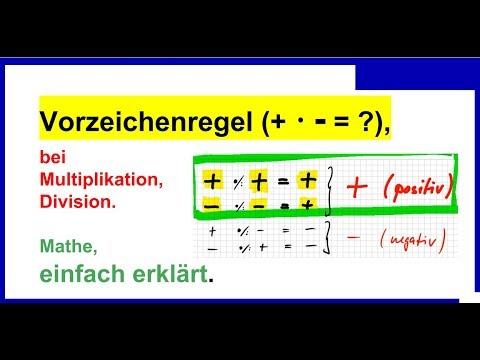
Bei der Multiplikation mit Vorzeichen gibt es bestimmte Regeln, die das Ergebnis bestimmen. Diese Regeln gelten für Zahlen mit Vorzeichen, also für ganze, rationale und reelle Zahlen.

1. Wenn man zwei Faktoren mit dem gleichen Vorzeichen multipliziert, erhält man ein positives Produkt. Das bedeutet, wenn beide Faktoren positiv sind oder beide negativ sind, ist das Ergebnis positiv.
Beispiel: (+5) · (+5) = +25

2. Wenn man zwei Faktoren mit unterschiedlichen Vorzeichen multipliziert, erhält man ein negatives Produkt. Das bedeutet, wenn einer der Faktoren positiv ist und der andere negativ ist, ist das Ergebnis negativ.
Beispiel: (+5) · (-5) = -25

3. Es gibt auch eine Regel für die Multiplikation von mehr als zwei Faktoren: Ein Produkt aus n Faktoren ist positiv, wenn es eine gerade Anzahl an negativen Faktoren enthält (0 wird als gerade angesehen). Ein Produkt aus n Faktoren ist negativ, wenn es eine ungerade Anzahl an negativen Faktoren enthält.
Beispiel: (+5) · (-1) · (-5) · (-2) · (+2) · (-5) · (+2) = +1000 (vier Mal Minus)
Beispiel: (-5) · (-1) · (-5) · (-2) · (+2) · (-5) · (+2) = -1000 (fünf Mal Minus)

Diese Regeln gelten auch für Divisionen, da jede Division als Multiplikation mit dem Kehrwert des Divisors geschrieben werden kann.

Es ist wichtig zu beachten, dass diese Regeln nur für Zahlen mit Vorzeichen gelten und nicht für natürliche Zahlen oder Bruchzahlen. Außerdem hat die Zahl 0 kein Vorzeichen, sie ist weder positiv noch negativ.

Zusammenfassend kann man sagen, dass die Multiplikation mit Vorzeichen bestimmte Ergebnisse liefert, abhängig von den Vorzeichen der Faktoren. Wenn beide Faktoren das gleiche Vorzeichen haben, ist das Produkt positiv. Wenn die Faktoren unterschiedliche Vorzeichen haben, ist das Produkt negativ.

Äquivalente Umformungen mit Plus und Minus

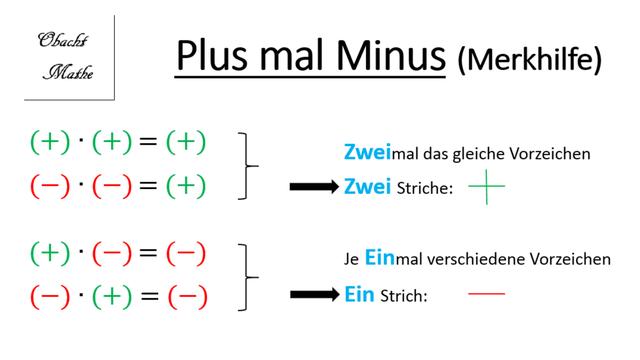
Äquivalente Umformungen mit Plus und Minus sind Rechenoperationen, bei denen die Vorzeichen von Zahlen verändert werden. Diese Umformungen sind wichtig, um mathematische Ausdrücke zu vereinfachen oder Gleichungen zu lösen.

Eine häufige äquivalente Umformung ist das Umkehren des Vorzeichens einer Zahl. Das negative Vorzeichen „–“ wandelt eine positive Zahl in eine negative um und umgekehrt. Zum Beispiel wird aus der Zahl 5 durch das Umkehren des Vorzeichens -5.

Eine weitere äquivalente Umformung ist das Entfernen des positiven Vorzeichens „+“. Da das positive Vorzeichen keine Veränderung bewirkt, wird es oft weggelassen, außer wenn man verdeutlichen möchte, dass hier kein negatives Vorzeichen steht.

Bei der Multiplikation gibt es ebenfalls äquivalente Umformungen mit Plus und Minus. Wenn zwei Faktoren mit dem gleichen Vorzeichen multipliziert werden, ergibt dies ein positives Produkt. Zum Beispiel ergibt (+5) · (+5) = +25.

Wenn hingegen zwei Faktoren mit unterschiedlichen Vorzeichen multipliziert werden, ergibt dies ein negatives Produkt. Zum Beispiel ergibt (+5) · (-5) = -25.

Diese äquivalenten Umformungen können auch auf Divisionen angewendet werden, indem man den Divisor als Kehrwert schreibt und dann die entsprechenden Regeln für die Multiplikation anwendet.

Es ist wichtig zu beachten, dass diese Regeln nur für ganze, rationale und reelle Zahlen gelten und nicht für natürliche Zahlen oder Bruchzahlen.

Zusammenfassend ermöglichen äquivalente Umformungen mit Plus und Minus das Vereinfachen von mathematischen Ausdrücken und das Lösen von Gleichungen. Durch das Ändern der Vorzeichen können positive Zahlen in negative umgewandelt werden und umgekehrt. Bei der Multiplikation ergeben gleiche Vorzeichen ein positives Produkt, während unterschiedliche Vorzeichen ein negatives Produkt ergeben.

Ausklammern von Vorzeichen: Wie wirken sich Plus und Minus aus?

Beim Ausklammern von Vorzeichen geht es darum, wie sich das Vorzeichen des Terms verändert, wenn man einen gemeinsamen Faktor ausklammert. Es gibt zwei mögliche Fälle:

1. Wenn alle Terme im Ausdruck positiv sind und der gemeinsame Faktor negativ ist, ändert sich das Vorzeichen aller Terme im ausgedrückten Term. Zum Beispiel:
\((-2) \cdot (x + 3) = -2x – 6\)

2. Wenn alle Terme im Ausdruck negativ sind und der gemeinsame Faktor negativ ist, ändert sich das Vorzeichen aller Terme im ausgedrückten Term. Zum Beispiel:
\((-2) \cdot (-x – 3) = 2x + 6\)

Es ist wichtig zu beachten, dass das Vorzeichen des gemeinsamen Faktors den Ausdruck beeinflusst und nicht die einzelnen Terme innerhalb des Ausdrucks.

Zusammenfassend lässt sich sagen, dass beim Ausklammern von Vorzeichen das Vorzeichen des gemeinsamen Faktors den gesamten Term beeinflusst und nicht die einzelnen Terme innerhalb des Terms.

Zusammenfassend kann gesagt werden, dass das Hinzufügen von Zahlen zu einer Summe führt, während das Subtrahieren von Zahlen eine Differenz ergibt. Plus und Minus sind grundlegende mathematische Operationen, die in verschiedenen Bereichen des täglichen Lebens angewendet werden können, um Ergebnisse zu erzielen oder Probleme zu lösen. Es ist wichtig, ein solides Verständnis dieser Konzepte zu haben, um effektiv mit Zahlen umgehen zu können.