Alles über senkrechte Linien: Definition, Zeichnung & Anwendungen

Senkrecht ist ein Begriff, der in der Geometrie verwendet wird, um eine Linie oder eine Fläche zu beschreiben, die im rechten Winkel zu einer anderen steht. Es bedeutet, dass zwei Objekte senkrecht zueinander sind, wenn sie sich im 90-Grad-Winkel schneiden. Diese Eigenschaft spielt eine wichtige Rolle in verschiedenen Bereichen wie Architektur, Mathematik und Physik. In diesem Artikel werden wir genauer erkunden, was es bedeutet, wenn etwas senkrecht ist und welche Konsequenzen dies haben kann.

Was bedeutet senkrecht und wie zeichnet man senkrechte Geraden?

Senkrecht zu sein bedeutet, dass zwei Linien oder Strecken einen rechten Winkel zueinander bilden. Ein rechter Winkel hat eine Größe von 90° und wird durch einen Viertelkreis mit einem Punkt gekennzeichnet. Um senkrechte Geraden zu zeichnen, kann man entweder ein Geodreieck oder einen Zirkel verwenden.

Mit einem Geodreieck kann man ganz einfach eine senkrechte Linie zu einer gegebenen Geraden einzeichnen. Dazu legt man die Mittellinie des Geodreiecks auf die gegebene Gerade und zeichnet entlang der Messleiste des Geodreiecks eine weitere Gerade.

Mit einem Zirkel kann man ebenfalls senkrechte Linien einzeichnen. Man beginnt damit, an irgendeinem Punkt auf der Geraden einzustechen und einen Kreis zu zeichnen. Dann stellt man den Zirkel etwas größer ein und sticht an einem der Schnittpunkte des Kreises mit der Geraden erneut ein. Man zeichnet einen weiteren Kreisbogen, der die Gerade schneidet. Dieser Schritt wird am anderen Schnittpunkt wiederholt. Schließlich zieht man eine Gerade durch die beiden Schnittpunkte der Kreisbögen.

Auch bei Vektoren kann von Senkrechtigkeit gesprochen werden. Zwei Vektoren sind senkrecht zueinander, wenn ihr Skalarprodukt Null ist. Das Skalarprodukt der Richtungsvektoren von zwei aufeinander senkrecht stehenden Geraden ist immer Null. Allerdings bedeutet ein Skalarprodukt von Null bei den Richtungsvektoren nicht automatisch, dass die Geraden senkrecht zueinander stehen können. Sie könnten auch windschief zueinander liegen.

In der Mathematik haben senkrechte Linien eine klare Definition und können mit verschiedenen Hilfsmitteln gezeichnet werden. Im Alltag wird der Begriff „senkrecht“ jedoch oft im Zusammenhang mit horizontalen, vertikalen und waagerechten Linien verwendet.

Senkrecht: Definition und Zeichnung von senkrechten Linien

Definition von Senkrecht

Um den Begriff „senkrecht“ zu verstehen, muss zunächst der rechte Winkel bekannt sein. Ein rechter Winkel ist genau 90° groß und wird durch einen Viertelkreis mit einem Punkt gekennzeichnet. Zwei Linien stehen senkrecht zueinander, wenn zwischen ihnen ein rechter Winkel liegt. Dies gilt auch für Geraden oder Strecken, die senkrecht aufeinander stehen.

Zeichnung von senkrechten Linien

Um eine senkrechte Linie zu einer gegebenen Geraden zu zeichnen, kann ein Geodreieck verwendet werden. Die Mittellinie des Geodreiecks wird dabei auf die gegebene Gerade gelegt und entlang der Messleiste des Geodreiecks wird eine weitere Gerade gezeichnet.

Mit einem Zirkel können ebenfalls senkrechte Linien gezeichnet werden. Dazu wird zunächst irgendwo auf der Geraden mit dem Zirkel eingestochen und ein Kreisbogen gezeichnet, der die Gerade zweimal schneidet. An einem der Schnittpunkte wird erneut eingestochen und ein weiterer Kreisbogen gezeichnet. Dies wird am anderen Schnittpunkt wiederholt. Die beiden Kreisbögen schneiden sich zweimal und eine Gerade kann durch diese Schnittpunkte gezogen werden.

Auch bei Geraden und Ebenen mit Vektoren kann von Senkrechtigkeit gesprochen werden. Zwei Vektoren sind senkrecht zueinander, wenn ihr Skalarprodukt 0 ist. Wenn zwei Geraden aufeinander senkrecht stehen, ist das Skalarprodukt ihrer Richtungsvektoren immer 0.

Es ist jedoch zu beachten, dass nur weil das Skalarprodukt der Richtungsvektoren 0 ist, nicht automatisch bedeutet, dass die Geraden senkrecht zueinander stehen. Sie können auch windschief zueinander liegen.

Zusammenfassend kann gesagt werden, dass senkrecht in der Mathematik eine spezifische Bedeutung hat und sich auf rechte Winkel und deren Beziehung zueinander bezieht. Es gibt verschiedene Methoden, um senkrechte Linien zu zeichnen, sowohl mit einem Geodreieck als auch mit einem Zirkel. Auch bei Vektoren und Ebenen kann von Senkrechtigkeit gesprochen werden.

Alles über Senkrechte: Bedeutung und Zeichnung von senkrechten Geraden

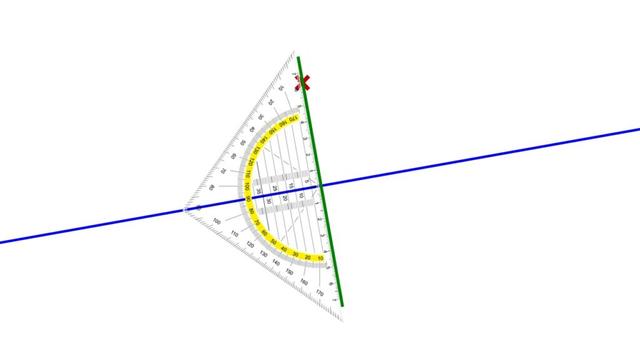
Was bedeutet eigentlich senkrecht?

Senkrecht bezeichnet eine Ausrichtung, bei der zwei Linien oder Strecken einen rechten Winkel (90°-Winkel) zueinander bilden. Ein rechter Winkel wird durch einen Viertelkreis mit einem Punkt markiert. Somit stehen zwei Linien senkrecht aufeinander, wenn zwischen ihnen ein rechter Winkel liegt.

Wie zeichnest du senkrechte Geraden?

Es gibt verschiedene Möglichkeiten, senkrechte Geraden zu zeichnen. Eine einfache Methode ist die Verwendung eines Geodreiecks. Dabei legt man die Mittellinie des Geodreiecks auf die gegebene Gerade und zieht entlang der Messleiste eine weitere Gerade. Alternativ kann man auch mit einem Zirkel arbeiten, indem man einen Kreis um die gegebene Gerade zeichnet und anschließend zwei Schnittpunkte markiert, durch die man eine Gerade zieht.

Zudem kann der Begriff „senkrecht“ auch auf Vektoren und Ebenen angewendet werden. Zwei Vektoren gelten als senkrecht zueinander, wenn ihr Skalarprodukt 0 ist. Bei geraden Linien in einer Ebene sind ihre Richtungsvektoren parallel zueinander, wenn das Skalarprodukt ihrer Richtungsvektoren ebenfalls 0 ist.

Es ist jedoch wichtig zu beachten, dass das Skalarprodukt alleine nicht ausreicht, um festzustellen, ob zwei Geraden tatsächlich senkrecht zueinander stehen. Es ist auch möglich, dass sie windschief zueinander liegen.

In der Alltagssprache wird der Begriff „senkrecht“ oft im Zusammenhang mit horizontalen, vertikalen und waagerechten Ausrichtungen verwendet.

Senkrecht in der Mathematik: Definition und Anleitung zum Zeichnen von senkrechten Linien

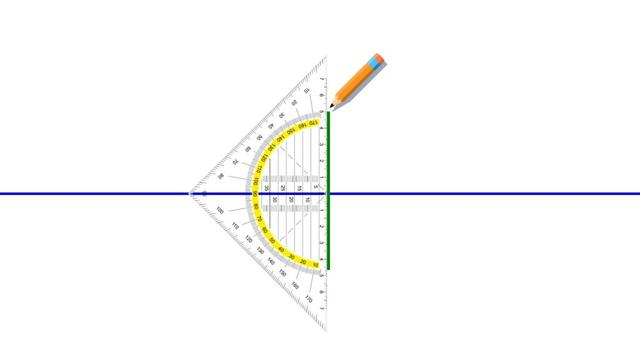
Definition von Senkrecht

Um den Begriff „senkrecht“ zu verstehen, muss man zunächst den rechten Winkel kennen. Ein rechter Winkel ist ein Winkel, der genau 90° groß ist und durch einen Viertelkreis mit einem Punkt gekennzeichnet wird. Zwei Linien stehen senkrecht aufeinander, wenn zwischen ihnen ein rechter Winkel (90°-Winkel) liegt. Dies gilt auch für Geraden oder Strecken.

Anleitung zum Zeichnen von senkrechten Linien

Es gibt verschiedene Möglichkeiten, um senkrechte Linien zu zeichnen:

1. Mit einem Geodreieck:
– Lege die Mittellinie des Geodreiecks auf die gegebene Gerade.
– Zeichne eine weitere Gerade entlang der Messleiste des Geodreiecks.

2. Mit einem Zirkel:
– Stich mit dem Zirkel irgendwo auf der Geraden ein und zeichne einen Kreis.
– Verändere die Größe des Zirkels nicht und stiche an den beiden Schnittpunkten des Kreises mit der Geraden erneut ein.
– Zeichne eine Gerade durch diese beiden Schnittpunkte.

3. Bei einer gegebenen Gerade und einem Punkt:
– Stich im Punkt auf der Geraden ein und zeichne einen Kreisbogen, der die Gerade zweimal schneidet.
– Stiche an den beiden Schnittpunkten erneut ein und zeichne eine Gerade durch diese beiden Schnittpunkte.

Senkrecht bei Geraden und Ebenen mit Vektoren

Bei Geraden und Ebenen mit Vektoren kann man ebenfalls von Senkrechtigkeit sprechen. Zwei Vektoren sind senkrecht zueinander, wenn ihr Skalarprodukt 0 ist. Wenn zwei Geraden aufeinander senkrecht stehen, ist das Skalarprodukt ihrer Richtungsvektoren immer 0. Es ist jedoch zu beachten, dass ein Skalarprodukt von 0 nicht automatisch bedeutet, dass die Geraden senkrecht zueinander stehen können.

Zusammenfassend lässt sich sagen, dass „senkrecht“ in der Mathematik eine spezifische Ausrichtung von Linien oder Vektoren beschreibt und durch einen rechten Winkel definiert wird. Es gibt verschiedene Methoden, um senkrechte Linien zu zeichnen, wie zum Beispiel mit einem Geodreieck oder einem Zirkel.

Verständnis von Senkrecht: Erklärung und Praxisbeispiele für das Zeichnen von senkrechten Geraden

Was bedeutet eigentlich senkrecht?

– Senkrecht bezieht sich auf zwei Linien oder Strecken, die einen rechten Winkel (90°) zueinander bilden.
– Ein rechter Winkel wird durch einen Viertelkreis mit einem Punkt gekennzeichnet.

Wie zeichnest du senkrechte Geraden?

– Um eine senkrechte Gerade zu einer gegebenen Gerade zu zeichnen, kannst du ein Geodreieck verwenden.
– Lege die Mittellinie des Geodreiecks auf die gegebene Gerade.
– Zeichne entlang der Messleiste des Geodreiecks eine weitere Gerade.
– Wenn du eine senkrechte Gerade durch einen Punkt zeichnen möchtest, kannst du ebenfalls ein Geodreieck verwenden.
– Lege die Mittellinie des Geodreiecks auf die gegebene Gerade.
– Schiebe das Geodreieck entlang der Geraden, bis der Punkt auf der Messleiste liegt.
– Zeichne eine Gerade entlang der Messleiste des Geodreiecks, sodass sie durch den Punkt geht.
– Mit einem Zirkel kannst du auch senkrechte Linien einzeichnen.
– Für eine senkrechte Linie zu einer gegebenen Geraden:
– Stich mit dem Zirkel irgendwo auf der Geraden ein und zeichne einen Kreis, der die Gerade zweimal schneidet.
– Stelle den Zirkel etwas größer ein und stich an einem der Schnittpunkte ein.
– Zeichne einen Kreisbogen, der die Gerade schneidet.
– Wiederhole den vorherigen Schritt am anderen Schnittpunkt.
– Zeichne eine Gerade durch die beiden Schnittpunkte.
– Für eine senkrechte Linie durch einen Punkt:
– Stich im Punkt mit dem Zirkel ein und zeichne einen Kreisbogen, der die Gerade zweimal schneidet.
– Stich an einem der Schnittpunkte ein und zeichne einen Kreisbogen, der die Gerade schneidet und durch den Punkt geht.
– Wiederhole den vorherigen Schritt am anderen Schnittpunkt.
– Zeichne eine Gerade durch die beiden Schnittpunkte.

Senkrechte in Bezug auf Vektoren und Ebenen

– Bei Vektoren sind zwei Vektoren senkrecht zueinander, wenn ihr Skalarprodukt 0 ist.
– Bei Geraden stehen diese senkrecht zueinander, wenn das Skalarprodukt ihrer Richtungsvektoren immer 0 ist. Beachte jedoch, dass das Gegenteil nicht gilt. Das Skalarprodukt kann 0 sein, obwohl die Geraden windschief zueinander liegen können.
– Bei Ebenen zeigt der Richtungsvektor einer Geraden senkrecht zur Normalenvektorform der Ebene, wenn sie in die gleiche Richtung zeigen (parallel sind).

Jetzt hast du alles über den Begriff „senkrecht“ gelernt und wie man senkrechte Linien zeichnet. Im Alltag wird dieser Begriff etwas anders verwendet, und er ist eng mit den Begriffen horizontal, vertikal und waagerecht verbunden. Wenn du mehr darüber erfahren möchtest, schau dir das verlinkte Video an!

Senkrecht in der Geometrie: Bedeutung und Techniken zum Zeichnen senkrechter Linien

Bedeutung von Senkrecht in der Geometrie

In der Geometrie bedeutet „senkrecht“ das Vorhandensein eines rechten Winkels zwischen zwei Linien oder Strecken. Ein rechter Winkel ist ein Winkel, der genau 90° misst und durch einen Viertelkreis mit einem Punkt gekennzeichnet wird. Wenn zwei Linien oder Strecken einen rechten Winkel bilden, stehen sie senkrecht zueinander.

Techniken zum Zeichnen senkrechter Linien

Es gibt verschiedene Techniken, um senkrechte Linien zu zeichnen:

1. Mit dem Geodreieck:
– Lege die Mittellinie des Geodreiecks auf die gegebene Gerade.
– Zeichne entlang der Messleiste des Geodreiecks eine weitere Gerade.

2. Mit dem Zirkel:
– Stich mit dem Zirkel irgendwo auf der Geraden ein und zeichne einen Kreis.
– Stelle den Zirkel etwas größer ein und stich an einem Schnittpunkt ein.
– Zeichne einen weiteren Kreisbogen, der die Gerade schneidet.
– Wiederhole den vorherigen Schritt am anderen Schnittpunkt.
– Verbinde die beiden Schnittpunkte mit einer Geraden.

3. Durch einen gegebenen Punkt:
– Stich mit dem Zirkel im gegebenen Punkt ein und zeichne einen Kreisbogen, der die Gerade zweimal schneidet.
– Stich an einem der Schnittpunkte ein und zeichne einen weiteren Kreisbogen, der die Gerade schneidet und durch den Punkt geht.
– Wiederhole den vorherigen Schritt am anderen Schnittpunkt.
– Verbinde die beiden Schnittpunkte mit einer Geraden.

Es ist auch möglich, von Senkrecht in Bezug auf Vektoren und Ebenen zu sprechen. Zwei Vektoren sind senkrecht zueinander, wenn ihr Skalarprodukt 0 ist. Bei Geraden bedeutet das Skalarprodukt der Richtungsvektoren immer 0, wenn sie senkrecht zueinander stehen. Bei Ebenen müssen die Richtungsvektoren der Geraden und der Normalenvektor der Ebene in die gleiche Richtung zeigen, um als senkrecht betrachtet zu werden.

Die Bedeutung des Begriffs „senkrecht“ bezieht sich auf eine rechtwinklige Ausrichtung oder Positionierung, bei der eine Linie oder Fläche im 90-Grad-Winkel zu einer gegebenen Referenz steht. Diese Eigenschaft ist in verschiedenen Kontexten wie Mathematik, Physik und Alltagsleben von großer Bedeutung. Es ist wichtig, den Unterschied zwischen senkrecht und parallel zu verstehen, um korrekte Interpretationen und Anwendungen vornehmen zu können.