„Punktsymmetrisch bedeutet, dass eine Figur oder ein Objekt um einen bestimmten Punkt gedreht wird und dabei ihre Form unverändert bleibt. In der Mathematik ist dies ein wichtiges Konzept, das in verschiedenen Bereichen wie Geometrie und Algebra Anwendung findet. Erfahren Sie mehr über die Bedeutung von Punktsymmetrie und seine praktischen Anwendungen.“
Was ist punktsymmetrisch? Eine Erklärung.
Punktsymmetrie bei geometrischen Figuren:
Eine Figur wird als punktsymmetrisch bezeichnet, wenn sie durch die Spiegelung an einem Punkt auf sich selbst abgebildet wird. Dieser Punkt wird auch als Symmetriepunkt oder Symmetriezentrum bezeichnet. Bei einer punktsymmetrischen Figur handelt es sich um eine Drehung der Figur um 180°. Die Symmetriepunkte sind diejenigen Punkte, die rot gekennzeichnet sind und sich nach der Spiegelung nicht verändern.
Beispiel: Ein Parallelogramm ist eine geometrische Figur, bei der gegenüberliegende Seiten parallel zueinander liegen. Wenn man ein Parallelogramm an seinem Symmetriepunkt spiegelt, bleibt es unverändert und ist somit punktsymmetrisch.
Punktsymmetrie bei Funktionen:
Auch Funktionen können punktsymmetrisch sein. Der Graph einer Funktion f(x) ist zum Punkt P=(x0,y0) punktsymmetrisch, wenn die Gleichung f(x0−x)−y0=−f(x0+x)+y0 erfüllt ist. Das bedeutet, dass der Funktionswert f(x) für den Abstand (x-x0) vom Symmetriepunkt gleich dem negativen Funktionswert für den Abstand (x+x0) ist.
Beispiel: Die Funktion f(x)=(x−2)^3−1 ist zum Punkt P(2|-1) punktsymmetrisch, da die Gleichung f(2−x)−(-1)=−f(2+x)+(-1) erfüllt ist.
Punktsymmetrie am Ursprung:
Ein Spezialfall der Punktsymmetrie ist die Symmetrie am Ursprung, also für den Punkt P=(0,0). In diesem Fall vereinfacht sich die Gleichung zu f(x)=-f(-x), da der Abstand zum Ursprung immer gleich bleibt.
Um eine beliebige Figur an einem Punkt zu spiegeln, werden nacheinander alle charakteristischen Punkte an diesem Punkt gespiegelt und anschließend entsprechend der Gestalt der Figur verbunden.
Punktsymmetrie: Definition und Bedeutung.
Definition:
Eine Figur heißt punktsymmetrisch, wenn sie durch die Spiegelung an einem Punkt, dem sogenannten Symmetriepunkt oder Symmetriezentrum, auf sich selbst abgebildet wird. Dabei handelt es sich um eine Drehung der Figur um 180°. Die jeweils rot gekennzeichneten Punkte sind die Symmetriepunkte der Figuren.
Bedeutung:
Die Punktsymmetrie ist ein wichtiges Konzept in der Geometrie und findet Anwendung in verschiedenen Bereichen. Sie ermöglicht es uns, bestimmte Eigenschaften von Figuren zu erkennen und zu beschreiben.
Ein Parallelogramm ist ein Beispiel für eine Figur mit Punktsymmetrie. Die gegenüberliegenden Seiten des Parallelogramms sind parallel zueinander, was bedeutet, dass sie den gleichen Abstand voneinander haben. Durch die Spiegelung an einem Symmetriepunkt des Parallelogramms werden alle charakteristischen Punkte auf sich selbst abgebildet.
Auch ein Kreis besitzt Punktsymmetrie. Alle Punkte auf der Linie des Kreises haben den gleichen Abstand zum Mittelpunkt des Kreises. Durch die Spiegelung am Mittelpunkt werden alle Punkte auf sich selbst abgebildet.
Die Punktsymmetrie kann auch auf Funktionen angewendet werden. Der Graph einer Funktion ist punktsymmetrisch zum Punkt P=(x0,y0), wenn die Gleichung f(x0−x)−y0=−f(x0+x)+y0 erfüllt ist. Dies bedeutet, dass die Funktion um den Punkt P symmetrisch ist.
Die Punktsymmetrie hat auch eine spezielle Bedeutung am Ursprung (P=(0,0)). In diesem Fall vereinfacht sich die Gleichung zu f(x)=-f(-x), was bedeutet, dass die Funktion achsensymmetrisch zur y-Achse ist.
Um eine beliebige Figur an einem Punkt zu spiegeln, werden nacheinander alle charakteristischen Punkte an diesem Punkt gespiegelt und schließlich entsprechend der Gestalt der Figur verbunden.
Die Punktsymmetrie ist ein wichtiges Konzept in der Geometrie und findet Anwendung bei der Beschreibung von symmetrischen Figuren und Funktionen. Es ermöglicht uns, bestimmte Eigenschaften von Figuren zu erkennen und zu analysieren.
Die Bedeutung von Punktsymmetrie in der Mathematik.

Punktsymmetrie bei Figuren
In der Mathematik bezeichnet die Punktsymmetrie eine Eigenschaft von Figuren. Eine Figur wird als punktsymmetrisch bezeichnet, wenn sie durch eine Spiegelung an einem bestimmten Punkt auf sich selbst abgebildet wird. Dieser Punkt wird als Symmetriepunkt oder Symmetriezentrum bezeichnet. Bei einer punktsymmetrischen Figur handelt es sich um eine Drehung der Figur um 180° um den Symmetriepunkt.
Punktsymmetrie bei Funktionen
Auch bei Funktionen kann die Punktsymmetrie eine Rolle spielen. Der Graph einer Funktion wird als punktsymmetrisch zum Punkt P=(x0,y0) bezeichnet, wenn für jeden Wert x gilt: f(x0-x)-y0 = -f(x0+x)+y0. Das bedeutet, dass die Funktionswerte f(x) und -f(x) bezüglich des Punktes P den gleichen Abstand haben.
Punktsymmetrie am Ursprung
Ein Spezialfall der Punktsymmetrie ist die Punktsymmetrie am Ursprung, also für den Punkt P=(0,0). In diesem Fall vereinfacht sich die Gleichung zu: f(-x) = -f(x). Das bedeutet, dass die Funktionswerte f(x) und -f(x) bezüglich des Ursprungs spiegelsymmetrisch sind.
Die Punktsymmetrie ist ein wichtiges Konzept in der Mathematik und findet Anwendung in verschiedenen Bereichen wie der Geometrie und der Funktionslehre. Sie ermöglicht es, Symmetrien von Figuren und Funktionen zu erkennen und zu beschreiben.
Punktsymmetrie: Eine genaue Beschreibung und Anwendung.
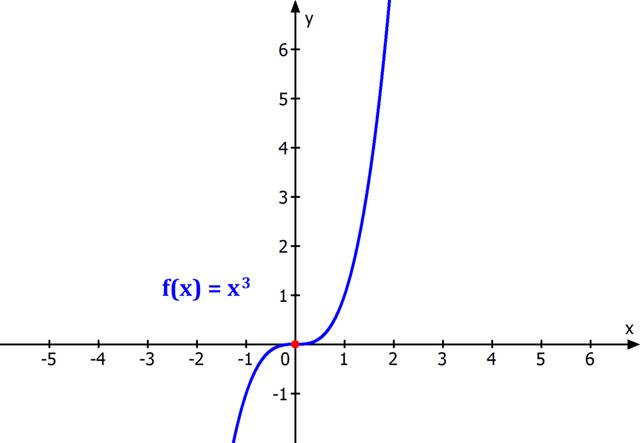
Beschreibung:
Die Punktsymmetrie bezieht sich auf die Eigenschaft einer Figur, dass sie durch die Spiegelung an einem bestimmten Punkt auf sich selbst abgebildet wird. Dieser Punkt wird als Symmetriepunkt oder Symmetriezentrum bezeichnet. Bei einer punktsymmetrischen Figur handelt es sich um eine Drehung der Figur um 180° um den Symmetriepunkt.
Eine Figur ist punktsymmetrisch, wenn alle Punkte der Figur den gleichen Abstand zum Symmetriepunkt haben und wenn die Verbindungslinien zwischen den entsprechenden Punkten nach der Spiegelung erhalten bleiben.
Ein Spezialfall der Punktsymmetrie ist die Symmetrie am Ursprung, also für den Punkt (0,0). In diesem Fall vereinfacht sich die Gleichung zur Darstellung der Punktsymmetrie.
Anwendung:
Die Punktsymmetrie findet in verschiedenen Bereichen Anwendung. Zum Beispiel in der Geometrie kann sie bei der Konstruktion von Figuren verwendet werden. Indem man charakteristische Punkte einer Figur an einem bestimmten Punkt spiegelt und diese dann entsprechend verbindet, kann man die gespiegelte Form der Figur erstellen.
In der Mathematik wird die Punktsymmetrie auch bei Funktionen verwendet. Eine Funktion f(x) ist punktsymmetrisch zum Punkt P=(x0,y0), wenn f(x0−x)−y0=−f(x0+x)+y0 gilt. Durch diese Eigenschaft können bestimmte Eigenschaften der Funktion bestimmt werden.
Die Punktsymmetrie ist ein wichtiges Konzept, das in verschiedenen Bereichen angewendet wird und dazu beiträgt, Symmetrien in Figuren und Funktionen zu erkennen und zu beschreiben.
Mathematische Konzepte: Was bedeutet punktsymmetrisch?
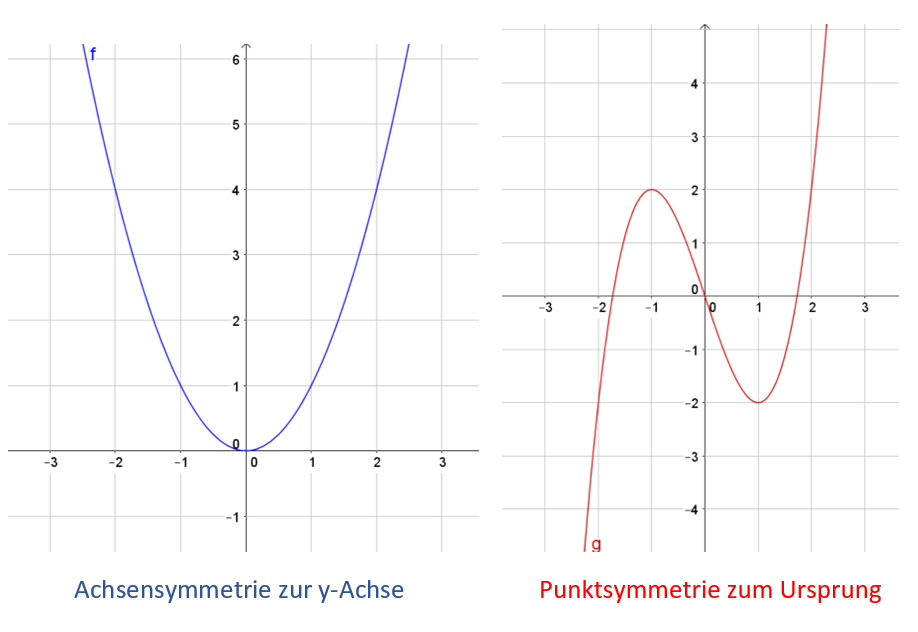
Wenn eine Figur punktsymmetrisch ist, bedeutet dies, dass sie durch die Spiegelung an einem Punkt auf sich selbst abgebildet wird. Dieser Punkt wird als Symmetriepunkt oder Symmetriezentrum bezeichnet. Eine punktsymmetrische Figur kann als Drehung der Figur um 180° betrachtet werden.
Ein Parallelogramm ist ein Viereck, bei dem gegenüberliegende Seiten parallel zueinander liegen. Ein Kreis hingegen ist eine geschlossene Linie um einen Mittelpunkt herum. Alle Punkte auf der Linie haben den gleichen Abstand oder Radius zum Mittelpunkt.
Der Graph einer Funktion ist punktsymmetrisch zum Punkt P=(x0,y0), wenn die Gleichung f(x0−x)−y0=−f(x0+x)+y0 erfüllt ist. Ein Spezialfall ist die Punktsymmetrie am Ursprung (P=(0,0)). In diesem Fall vereinfacht sich die Gleichung zu f(x)=-f(-x).
Symmetrie in der Geometrie: Die Bedeutung von Punktsymmetrie erklärt.
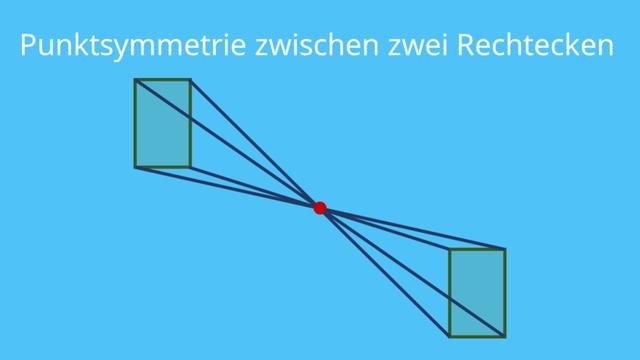
Was ist Punktsymmetrie?
Die Punktsymmetrie ist eine Form der Symmetrie in der Geometrie. Sie tritt auf, wenn eine Figur durch die Spiegelung an einem bestimmten Punkt auf sich selbst abgebildet wird. Dieser Punkt wird als Symmetriepunkt oder Symmetriezentrum bezeichnet. Bei einer punktsymmetrischen Figur handelt es sich um eine Drehung der Figur um 180 Grad.
Beispiele für Punktsymmetrie
Ein Beispiel für eine punktsymmetrische Figur ist ein Parallelogramm. In einem Parallelogramm liegen die gegenüberliegenden Seiten parallel zueinander. Wenn man das Parallelogramm an seinem Symmetriepunkt spiegelt, bleibt es unverändert.
Ein weiteres Beispiel für Punktsymmetrie ist ein Kreis. Ein Kreis ist eine geschlossene Linie um einen Mittelpunkt, bei dem alle Punkte auf der Linie den gleichen Abstand zum Mittelpunkt haben. Wenn man einen Kreis an seinem Mittelpunkt spiegelt, bleibt er ebenfalls unverändert.
Punktsymmetrie am Ursprung
Ein spezieller Fall der Punktsymmetrie ist die Symmetrie am Ursprung, also wenn der Symmetriepunkt (0,0) ist. In diesem Fall vereinfacht sich die Gleichung zur Bestimmung der Punktsymmetrie einer Funktion zu f(x) = -f(-x). Das bedeutet, dass die Funktionswerte für positive und negative x-Werte jeweils das negative Vorzeichen haben.
Um eine beliebige Figur an einem Punkt zu spiegeln, werden nacheinander alle charakteristischen Punkte an diesem Punkt gespiegelt und anschließend entsprechend der Gestalt der Figur verbunden. Dies ermöglicht es, die Symmetrie einer Figur zu erkennen und zu beschreiben.
Zusammenfassend bedeutet punktsymmetrisch, dass eine Figur oder Funktion um einen bestimmten Punkt gespiegelt werden kann und dabei ihre Form unverändert bleibt. Dieses Konzept findet Anwendung in verschiedenen Bereichen wie Geometrie und Algebra und ermöglicht es, Symmetrie in mathematischen Objekten zu beschreiben.

