Erfahren Sie, wann eine Zahl durch 3 teilbar ist – bettermarks.

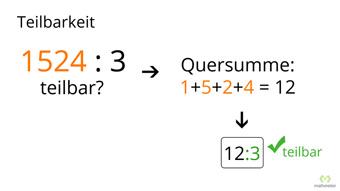
In der Mathematik ist eine Zahl genau dann durch 3 teilbar, wenn die Quersumme der Zahl selbst durch 3 teilbar ist. Dieser einfache Zusammenhang ermöglicht es uns, schnell zu überprüfen, ob eine gegebene Zahl ohne Rest durch 3 teilbar ist oder nicht. In diesem Artikel werden wir diesen Sachverhalt genauer betrachten und einige Beispiele für die Teilbarkeit durch 3 diskutieren.

Die Teilbarkeit durch 3: Wann ist eine Zahl durch 3 teilbar?

Teilbarkeitsregel für die Zahl 3:

Eine Zahl ist genau dann durch 3 teilbar, wenn die Quersumme dieser Zahl ebenfalls durch 3 teilbar ist. Die Quersumme einer Zahl erhält man, indem man alle Ziffern der Zahl addiert.

Beispiel:
Die Zahl 315 ist durch 3 teilbar, da ihre Quersumme (3+1+5=9) ebenfalls durch 3 teilbar ist.

Weitere Eigenschaften der Teilbarkeit durch 3:

– Wenn eine Zahl bereits durch 9 teilbar ist, dann ist sie auch automatisch durch 3 teilbar.
– Die Summe zweier Zahlen, die beide durch 3 teilbar sind, ist ebenfalls durch 3 teilbar.
– Die Differenz zweier Zahlen, von denen eine durch 3 teilbar ist und die andere nicht, ist nicht durch 3 teilbar.

Es gibt also verschiedene Möglichkeiten festzustellen, ob eine Zahl ohne Rest durch 3 teilbar ist. Diese Regel kann in der Mathematik verwendet werden, um Teilbarkeiten zu überprüfen und Rechenaufgaben zu vereinfachen.

Teilbarkeitsregeln: Wie erkenne ich, ob eine Zahl durch 3 teilbar ist?

1. Die Quersumme

Eine einfache Methode, um herauszufinden, ob eine Zahl durch 3 teilbar ist, besteht darin, die Quersumme der Zahl zu berechnen. Dazu addiert man alle Ziffern der Zahl zusammen. Ist das Ergebnis dieser Addition durch 3 teilbar, so ist auch die ursprüngliche Zahl durch 3 teilbar.

Beispiel: Betrachten wir die Zahl 246. Die Quersumme dieser Zahl ist 2 + 4 + 6 = 12. Da 12 ohne Rest durch 3 teilbar ist, ist auch die Zahl 246 durch 3 teilbar.

2. Die Teilbarkeitsregel

Eine weitere Möglichkeit, um festzustellen, ob eine Zahl durch 3 teilbar ist, besteht in der Anwendung der Teilbarkeitsregel. Diese besagt, dass eine natürliche Zahl genau dann durch 3 teilbar ist, wenn ihre Quersumme ebenfalls durch 3 teilbar ist.

Beispiel: Nehmen wir die Zahl 567. Ihre Quersumme beträgt 5 + 6 +7 =18. Da auch die Quersumme von 18 wiederum durch 3 ohne Rest teilbar ist, können wir schließen, dass die Zahl 567 ebenfalls durch 3 ohne Rest teilbar ist.

Es gibt noch weitere Teilbarkeitsregeln für andere Zahlen wie beispielsweise die Teilbarkeit durch 6 und die Teilbarkeit durch9. Diese Regeln können helfen zu erkennen, ob eine bestimmte Zahl ohne Rest durch eine andere Zahl teilbar ist.

Mathebuch: Alles über die Teilbarkeit von Zahlen durch 3

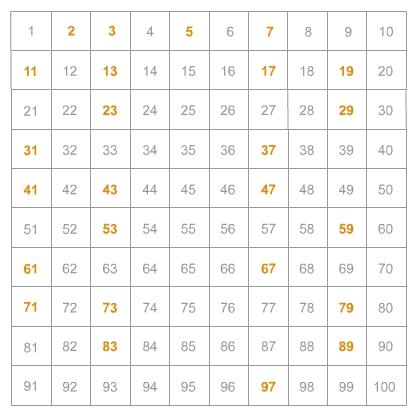
Was bedeutet Teilbarkeit durch 3?

Die Teilbarkeit einer Zahl durch 3 bedeutet, dass diese Zahl ohne Rest durch 3 geteilt werden kann. Anders ausgedrückt, eine Zahl ist durch 3 teilbar, wenn bei der Division durch 3 kein Rest übrig bleibt. Zum Beispiel ist die Zahl 12 durch 3 teilbar, da sie ohne Rest durch 3 geteilt werden kann (12 ÷ 3 = 4).

Teilbarkeitsregeln für die Zahl 3

Um zu überprüfen, ob eine Zahl durch 3 teilbar ist, gibt es einige Teilbarkeitsregeln:
– Die Quersumme einer Zahl muss durch 3 teilbar sein. Das bedeutet, dass man alle Ziffern der Zahl addiert und das Ergebnis dann wiederum durch 3 teilt. Wenn das Ergebnis eine ganze Zahl ergibt, ist die Ausgangszahl auch durch 3 teilbar.
– Eine zweistellige oder größere Zahl kann als Summe ihrer Ziffern dargestellt werden. Wenn diese Summe dann wiederum durch 3 teilbar ist, ist auch die Ausgangszahl selbst durch 3 teilbar.
– Eine weitere Regel besagt, dass eine ungerade Potenz von drei (wie zum Beispiel 9 oder 27) immer selbst auch eine Teilerin der Zahl ist.

Es gibt noch weitere Eigenschaften und Regeln zur Teilbarkeit von Zahlen durch 3, aber diese Grundregeln helfen bereits dabei zu bestimmen, ob eine bestimmte Zahl ohne Rest durch 3 teilbar ist oder nicht.

Bettermarks: Effektives Lernen der Teilbarkeit durch 3

Personalisiertes Lernen für Schülerinnen und Schüler

Bettermarks bietet eine effektive Möglichkeit, die Teilbarkeit durch 3 zu erlernen. Mit den adaptiven Übungen können Schülerinnen und Schüler auf verschiedenen Geräten wie Tablets, Computern und Smartphones rechnen. Dabei erhalten sie personalisierte Rückmeldungen, die ihnen helfen, ihr Verständnis für das Thema zu verbessern. Durch regelmäßiges Üben können sie ihre Fähigkeiten in der Teilbarkeit durch 3 kontinuierlich steigern.

Erfolgreiche Studie in Uruguay

Die Regierung von Uruguay führte eine dreijährige Studie zur Nutzung von Bettermarks basierend auf UNESCO-Daten durch. Das Ergebnis war beeindruckend: Die Schülerinnen und Schüler, die Bettermarks verwendet haben, zeigten einen Lernzuwachs von bis zu 30%. Dies zeigt deutlich, dass das Lernen mit Bettermarks effektiv ist und positive Ergebnisse erzielen kann.

Weite Verbreitung in verschiedenen Ländern

Bettermarks wird nicht nur in Deutschland eingesetzt, sondern auch in den Niederlanden, Uruguay und Südafrika täglich im Unterricht verwendet. Es ist in vier Sprachen verfügbar und ermöglicht es Schülerinnen und Schülern weltweit, ihre mathematischen Fähigkeiten zu verbessern. Im Schuljahr 20/21 haben über 400.000 deutsche Schülerinnen und Schüler mit Bettermarks gerechnet und dabei mehr als 144 Millionen Aufgaben gelöst. Dies zeigt die hohe Akzeptanz und Beliebtheit von Bettermarks als Lernplattform für die Teilbarkeit durch 3.

Studie belegt: Bis zu 30% Lernzuwachs bei der Teilbarkeit durch 3 mit Bettermarks

Eine dreijährige Studie in Uruguay

Die Regierung von Uruguay hat eine dreijährige Studie durchgeführt, um die Nutzung von Bettermarks im Mathematikunterricht zu untersuchen. Dabei wurden Daten der UNESCO verwendet. Das Ergebnis dieser Studie war beeindruckend: Schülerinnen und Schüler, die Bettermarks zur Übung der Teilbarkeit durch 3 genutzt haben, konnten einen Lernzuwachs von bis zu 30% verzeichnen.

Über 400.000 Schülerinnen und Schüler in Deutschland nutzen Bettermarks

Im Schuljahr 20/21 haben über 400.000 Schülerinnen und Schüler in Deutschland mit Bettermarks gearbeitet. Insgesamt wurden mehr als 144 Millionen Aufgaben gelöst. Diese Zahlen zeigen deutlich, dass Bettermarks eine beliebte und effektive Methode ist, um mathematische Fähigkeiten zu verbessern.

Bettermarks weltweit im Einsatz

Bettermarks wird nicht nur in Deutschland, sondern auch in anderen Ländern wie den Niederlanden, Uruguay und Südafrika täglich im Unterricht eingesetzt. Die Tatsache, dass das Programm in vier Sprachen verfügbar ist, macht es für Schulen auf der ganzen Welt attraktiv. Durch die Möglichkeit, auf Tablets, Computern und Smartphones zu rechnen und personalisierte Rückmeldungen zu erhalten, bietet Bettermarks den Schülerinnen und Schülern eine flexible und interaktive Lernerfahrung.

Zahlreiche Schülerinnen und Schüler nutzen Bettermarks zur Übung der Teilbarkeit durch 3

1. Absatz:

Bettermarks ist eine beliebte Plattform, die von vielen Schülerinnen und Schülern genutzt wird, um ihre Kenntnisse in Mathematik zu verbessern. Insbesondere die Übung der Teilbarkeit durch 3 ist ein häufiges Thema, das auf Bettermarks geübt wird. Durch die adaptiven Übungen können die Schülerinnen und Schüler auf ihrem Tablet, Computer oder Smartphone rechnen und erhalten personalisierte Rückmeldungen zu ihren Aufgaben.

2. Absatz:

Die Regierung von Uruguay hat eine dreijährige Studie durchgeführt, um die Nutzung von Bettermarks in Schulen zu untersuchen. Basierend auf UNESCO-Daten wurde festgestellt, dass der Einsatz von Bettermarks zu einem Lernzuwachs von bis zu 30% führt. Dies zeigt deutlich den positiven Einfluss dieser Plattform auf das Lernen der Schülerinnen und Schüler.

3. Absatz:

Auch in Deutschland erfreut sich Bettermarks großer Beliebtheit. Im Schuljahr 20/21 haben über 400.000 Schülerinnen und Schüler mit Bettermarks gearbeitet und dabei mehr als 144 Millionen Aufgaben gelöst. Die Plattform ist in vier Sprachen verfügbar und wird nicht nur in Deutschland, sondern auch in den Niederlanden, Uruguay und Südafrika täglich im Unterricht eingesetzt. Dies zeigt, dass Bettermarks international anerkannt ist und einen wertvollen Beitrag zur Verbesserung des mathematischen Verständnisses von Schülerinnen und Schülern leistet.

Eine Zahl ist durch 3 teilbar, wenn ihre Quersumme ebenfalls durch 3 teilbar ist. Somit können wir ein einfaches Kriterium verwenden, um festzustellen, ob eine Zahl ohne langwierige Berechnungen durch 3 teilbar ist oder nicht.