Ein Baumdiagramm ist eine grafische Darstellung, die verwendet wird, um verschiedene Möglichkeiten oder Verzweigungen eines Ereignisses zu visualisieren. Es besteht aus einem Stamm, der das Hauptereignis darstellt, und Zweigen, die die verschiedenen möglichen Ergebnisse repräsentieren. Baumdiagramme werden häufig in Mathematik, Statistik und Entscheidungsfindung verwendet, um komplexe Situationen übersichtlich darzustellen und Lösungswege zu analysieren.
1. Einführung in das Baumdiagramm: Definition und Anwendung
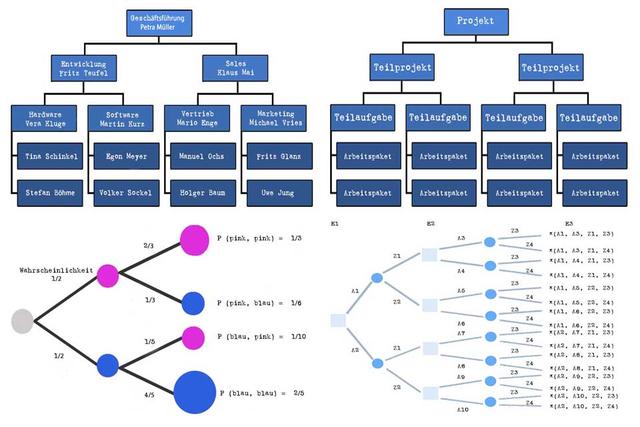
Ein Baumdiagramm ist ein Hilfsmittel zur graphischen Darstellung von zueinander in Beziehung stehenden Ergebnissen innerhalb der Wahrscheinlichkeitsrechnung. Es ermöglicht mit Hilfe der Pfadregeln Zufallsexperimente übersichtlich abzubilden und die dazugehörigen Wahrscheinlichkeiten zu berechnen.
– Ein Baumdiagramm besteht aus Stufen, die die verschiedenen Durchgänge eines Zufallsexperiments darstellen.
– Die Ereignisse, die eintreten können, werden als Kreise dargestellt.
– Die Linien, die die Ereignisse verbinden, werden Pfade genannt und bestehen aus den einzelnen Zweigen des Wahrscheinlichkeitsbaums.
– An den Zweigen müssen die jeweiligen Zweigwahrscheinlichkeiten abgetragen werden.
– Die Produktregel wird angewendet, um die Wahrscheinlichkeit eines bestimmten Versuchsausgangs zu berechnen.
– Die Summenregel wird verwendet, um die Wahrscheinlichkeit mehrerer Versuchsausgänge zu berechnen.
Das Baumdiagramm kann für verschiedene Zufallsexperimente wie das Werfen einer Münze oder eines Würfels verwendet werden. Es kann auch bei komplexeren Experimenten wie Urnenmodellen oder dem Ziegenproblem angewendet werden.
Ein Beispiel für die Anwendung des Baumdiagramms ist das Ziegenproblem bei Quizshows. Hierbei muss ein Kandidat eine von drei Türen auswählen, hinter denen sich entweder eine Ziege oder der Hauptgewinn befindet. Durch das Erstellen eines Baumdiagramms können die Wahrscheinlichkeiten für verschiedene Entscheidungen berechnet und rationale Entscheidungen getroffen werden.
Zusammenfassend ist das Baumdiagramm ein einfaches und flexibles Hilfsmittel der Wahrscheinlichkeitsrechnung, um Zufallsexperimente übersichtlich darzustellen und die dazugehörigen Wahrscheinlichkeiten zu berechnen. Es kann sowohl für einfache als auch für komplexe Experimente verwendet werden.
2. Schritt-für-Schritt-Anleitung zur Erstellung eines Baumdiagramms
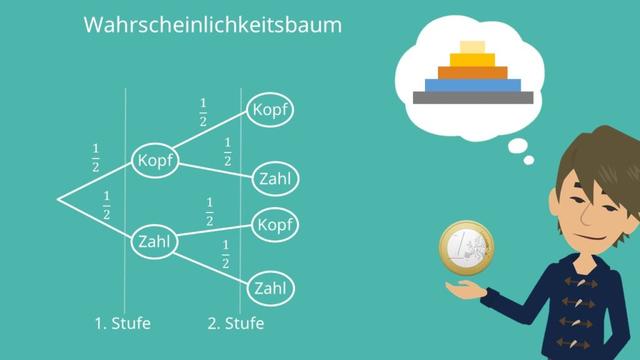
2. Schritt-für-Schritt-Anleitung zur Erstellung eines Baumdiagramms:
1. Überlege dir, wie viele Stufen das Baumdiagramm haben soll. Dies hängt von der Anzahl der Durchführungen des Zufallsexperiments ab.
2. Bestimme die möglichen Ereignisse, die eintreten können, und zeichne sie als Kreise im Baumdiagramm ein.
3. Verbinde die Ereignisse mit Linien, um Pfade zu erstellen. Diese Pfade repräsentieren die verschiedenen Möglichkeiten oder Ergebnisse des Experiments.
4. Trage entlang der Pfade die entsprechenden Zweigwahrscheinlichkeiten ein. Diese geben an, mit welcher Wahrscheinlichkeit ein bestimmtes Ereignis eintreten kann.
5. Berechne die Wahrscheinlichkeiten für verschiedene Ergebnisse, indem du entlang der Pfade gehst und die Zweigwahrscheinlichkeiten multiplizierst (bei Anwendung der Produktregel) oder addierst (bei Anwendung der Summenregel).
6. Kontrolliere deine Berechnungen, indem du sicherstellst, dass alle Wahrscheinlichkeiten eines Ereignisses zusammenaddiert 1 ergeben.
7. Wiederhole diese Schritte für verschiedene Szenarien oder Experimente, um weitere Ergebnisse zu berechnen.
Das Baumdiagramm ist ein nützliches Werkzeug in der Wahrscheinlichkeitsrechnung und ermöglicht eine übersichtliche Darstellung von mehrstufigen Zufallsexperimenten sowie die Berechnung dazugehöriger Wahrscheinlichkeiten.
3. Beispiele für die Anwendung des Baumdiagramms in der Wahrscheinlichkeitsrechnung
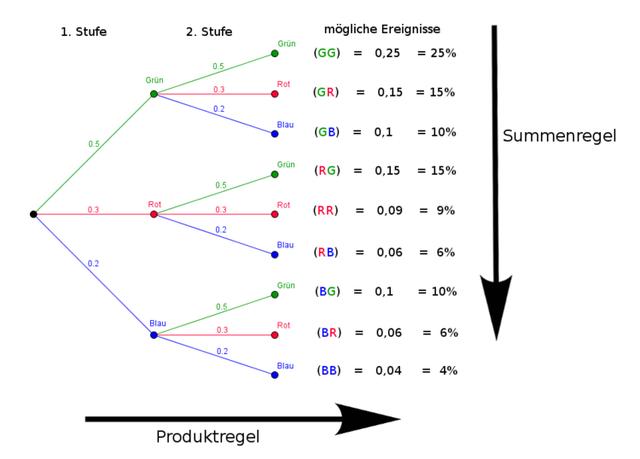
3. Beispiele für die Anwendung des Baumdiagramms in der Wahrscheinlichkeitsrechnung:
– Beispiel 1: Werfen einer Münze zweimal
In diesem Beispiel kann das Baumdiagramm verwendet werden, um die Wahrscheinlichkeit verschiedener Ergebnisse beim zweimaligen Werfen einer Münze zu berechnen. Die Ereignisse sind Kopf und Zahl, und die Zweigwahrscheinlichkeit beträgt jeweils 0,5. Mit Hilfe der Produktregel kann man zum Beispiel die Wahrscheinlichkeit berechnen, dass zweimal hintereinander Zahl geworfen wird.
– Beispiel 2: Ziegenproblem bei Quizshows
Das Ziegenproblem kann durch ein Baumdiagramm graphisch dargestellt werden und ermöglicht es, rationale Entscheidungen bei Quizshows zu begründen. Hier muss der Kandidat eine von drei Türen auswählen, hinter denen sich entweder Nieten (eine Ziege) oder der Hauptgewinn (ein Auto) befindet. Durch das Baumdiagramm können die dazugehörigen Wahrscheinlichkeiten abgetragen werden und beantworten so die Frage, ob es für den Kandidaten vorteilhaft ist, bei seiner Entscheidung zu bleiben.
– Beispiel 3: Urnenmodell
Das Baumdiagramm kann auch verwendet werden, um Zufallsexperimente basierend auf dem Urnenmodell darzustellen und deren Wahrscheinlichkeit zu berechnen. Nehmen wir an, in einer Urne befinden sich 2 blaue und 8 rote Kugeln. Wenn dreimal nacheinander eine Kugel ohne Zurücklegen gezogen wird, kann das Baumdiagramm genutzt werden, um die Wahrscheinlichkeit verschiedener Ergebnisse zu berechnen, z.B. die Wahrscheinlichkeit, erst zwei blaue und dann eine rote Kugel zu ziehen.
Diese Beispiele zeigen, wie das Baumdiagramm in der Wahrscheinlichkeitsrechnung angewendet werden kann, um komplexe Zufallsexperimente übersichtlich darzustellen und die dazugehörigen Wahrscheinlichkeiten zu berechnen.
4. Die Produktregel: Wie man die Wahrscheinlichkeit eines bestimmten Versuchsausgangs im Baumdiagramm berechnet
Die Produktregel ist eine wichtige Regel in der Wahrscheinlichkeitsrechnung und wird auch als erste Pfadregel bezeichnet. Sie besagt, dass die Wahrscheinlichkeit eines bestimmten Versuchsausgangs im Baumdiagramm durch das Produkt der einzelnen Zweigwahrscheinlichkeiten berechnet werden kann.
Um die Produktregel anzuwenden, muss man den entsprechenden Pfad im Baumdiagramm entlanggehen und die Wahrscheinlichkeiten der einzelnen Zweige multiplizieren. Das Ergebnis ist dann die Wahrscheinlichkeit des gewünschten Versuchsausgangs.
Ein Beispiel zur Verdeutlichung: Angenommen, wir werfen zweimal eine Münze. Wir möchten die Wahrscheinlichkeit berechnen, dass beide Male Kopf geworfen wird. Dazu gehen wir im Baumdiagramm den Pfad entlang, der zu diesem Ergebnis führt, und multiplizieren die beiden Zweigwahrscheinlichkeiten für Kopf (beide 0,5). Das Ergebnis ist 0,25 oder 25%.
Die Produktregel wird angewendet, wenn der Versuchsausgang und die dazugehörigen Wahrscheinlichkeiten mit dem logischen Operator „UND“ verknüpft sind. Man kann sich merken: Bei „UND“ muss man multiplizieren.
Die Anwendung der Produktregel ermöglicht es uns also, die Wahrscheinlichkeit bestimmter Versuchsausgänge in komplexeren Zufallsexperimenten zu berechnen.
5. Die Summenregel: Wie man die Wahrscheinlichkeit mehrerer Versuchsausgänge im Baumdiagramm berechnet
Die Summenregel ist eine wichtige Regel in der Wahrscheinlichkeitsrechnung, die verwendet wird, um die Wahrscheinlichkeit mehrerer Versuchsausgänge im Baumdiagramm zu berechnen. Sie wird auch als Additionsregel oder zweite Pfadregel bezeichnet.
Um die Summenregel anzuwenden, müssen die Pfadwahrscheinlichkeiten der einzelnen Ergebnisse addiert werden. Wenn also ein Ereignis mehrere mögliche Ergebnisse umfasst und diese Ergebnisse mit ODER verknüpft sind, kann man die Summenregel verwenden.
Ein Beispiel für die Anwendung der Summenregel wäre das Werfen eines Würfels. Wenn wir wissen möchten, mit welcher Wahrscheinlichkeit entweder eine 2 oder eine 4 geworfen wird, können wir die Wahrscheinlichkeiten dieser beiden Ergebnisse addieren. Die Wahrscheinlichkeit für eine 2 beträgt 1/6 und die Wahrscheinlichkeit für eine 4 beträgt ebenfalls 1/6. Daher ergibt sich insgesamt eine Wahrscheinlichkeit von 1/6 + 1/6 = 1/3.
Es ist wichtig zu beachten, dass die Summenregel nur dann angewendet werden kann, wenn die Ereignisse disjunkt sind, das heißt sie schließen sich gegenseitig aus. In unserem Beispiel können wir entweder eine 2 oder eine 4 werfen, aber nicht beides gleichzeitig.
Die Anwendung der Summenregel im Baumdiagramm ermöglicht es uns, komplexe Zufallsexperimente übersichtlich darzustellen und ihre Wahrscheinlichkeiten einfach zu berechnen. Es ist ein nützliches Werkzeug in der Wahrscheinlichkeitsrechnung und findet Anwendung in vielen verschiedenen Bereichen wie der Statistik, der Stochastik oder der Entscheidungstheorie.
6. Anwendungen des Baumdiagramms: Das Ziegenproblem und andere komplexe Zufallsexperimente
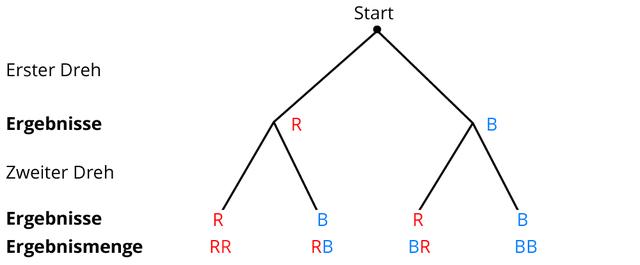
Das Baumdiagramm ist ein nützliches Werkzeug, um komplexe Zufallsexperimente in der Wahrscheinlichkeitsrechnung darzustellen. Es ermöglicht uns, die verschiedenen Ergebnisse übersichtlich abzubilden und die dazugehörigen Wahrscheinlichkeiten zu berechnen.
Ein Beispiel für eine Anwendung des Baumdiagramms ist das Ziegenproblem. Bei diesem Problem muss ein Kandidat eine von drei Türen auswählen, hinter denen sich entweder eine Ziege oder der Hauptgewinn (ein Auto) befindet. Nachdem eine Ziegentür geöffnet wurde, muss der Kandidat entscheiden, ob er bei seiner ausgewählten Tür bleiben möchte oder nicht. Durch das Baumdiagramm können wir die Wahrscheinlichkeiten für verschiedene Entscheidungen berechnen und somit rational begründete Entscheidungen treffen.
Das Baumdiagramm kann auch für andere komplexe Zufallsexperimente wie Urnenmodelle verwendet werden. Stellen wir uns vor, in einer Urne befinden sich 2 blaue und 8 rote Kugeln. Wenn wir nacheinander dreimal eine Kugel ziehen, ohne sie zurückzulegen, können wir mit Hilfe des Baumdiagramms die Wahrscheinlichkeit für verschiedene Ergebnisse berechnen.
Das Baumdiagramm ist ein vielseitiges Werkzeug in der Wahrscheinlichkeitsrechnung und findet Anwendung in vielen Bereichen wie der Stochastik und Statistik. Es ermöglicht uns, komplexe Zusammenhänge übersichtlich darzustellen und die Wahrscheinlichkeiten für verschiedene Ergebnisse zu berechnen.
Zusammenfassend lässt sich sagen, dass ein Baumdiagramm eine grafische Darstellungsmethode ist, um Wahrscheinlichkeiten und mögliche Ergebnisse von Ereignissen zu veranschaulichen. Es bietet eine einfache Möglichkeit, komplexe Entscheidungsprozesse zu analysieren und ermöglicht es uns, fundierte Entscheidungen zu treffen.

