„Orthogonal“ ist ein Begriff aus der Mathematik und bedeutet „senkrecht“ oder „rechtwinklig“. In verschiedenen Fachgebieten wie der Geometrie, der linearen Algebra oder der Signalverarbeitung spielt dieser Begriff eine wichtige Rolle. Erfahren Sie hier mehr über die Definition und Anwendung von orthogonalen Konzepten und Vektoren.
Was bedeutet orthogonal? Alles, was du wissen musst!
Orthogonalität in der Ebene
Orthogonalität bezieht sich auf die Beziehung zwischen zwei Geraden in der Ebene. Zwei Geraden g und h gelten als orthogonal zueinander, wenn sie sich im rechten Winkel (90°) schneiden. Diese senkrechte Beziehung kann auch mit dem Symbol „⊥“ dargestellt werden. Um die Orthogonalität zu überprüfen, misst man den Winkel zwischen den beiden Geraden und stellt sicher, dass er 90° beträgt.
Orthogonalität im Raum
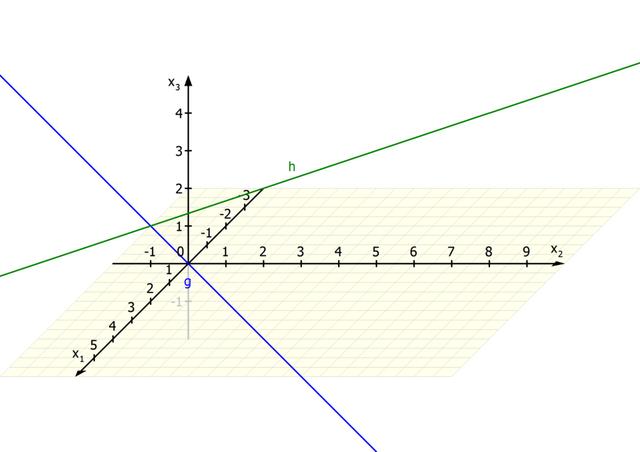
Im dreidimensionalen Raum gibt es ebenfalls den Begriff der Orthogonalität. Allerdings können sich die Geraden in unterschiedlichen Ebenen befinden, wodurch das Messen des Winkels schwierig wird. Hier kommen Vektoren ins Spiel. Die Richtungsvektoren der Geraden werden verwendet, um das Skalarprodukt zu berechnen. Wenn das Skalarprodukt 0 ergibt, sind die Geraden orthogonal zueinander.
Es ist wichtig zu beachten, dass im Raum zwei orthogonale Geraden nicht unbedingt einen Schnittpunkt haben müssen. Die Orthogonalität bezieht sich hier nur auf die Richtungen der Geraden.
Orthogonalität von Ebenen
Ebenen können ebenfalls orthogonal zueinander stehen oder von Geraden geschnitten werden. Um dies zu überprüfen, verwendet man Normalenvektoren. Diese können entweder direkt abgelesen oder mithilfe des Kreuzprodukts aus den Richtungsvektoren einer Ebene berechnet werden. Wenn das Skalarprodukt der Normalenvektoren 0 ergibt, sind die Ebenen senkrecht zueinander.
Die Reihenfolge der Benennung von Geraden oder Ebenen ist dabei egal. Wenn g orthogonal zu h ist, dann ist auch h orthogonal zu g. Eine Gerade steht genau dann orthogonal auf einer Ebene, wenn sie parallel zu deren Normalenvektor ist.
Jetzt weißt du alles, was du über Orthogonalität wissen musst!
Orthogonale Geraden: Eigenschaften und Bedeutung
Eigenschaften orthogonaler Geraden:
- Orthogonale Geraden schneiden sich im rechten Winkel (90°).
- Sie liegen in einer Ebene.
- Die Richtungsvektoren der beiden Geraden stehen senkrecht aufeinander.
Orthogonale Geraden haben spezielle Eigenschaften, die es ermöglichen, sie voneinander zu unterscheiden. Eine wichtige Eigenschaft ist, dass sich orthogonale Geraden im rechten Winkel schneiden. Dies bedeutet, dass der Winkel zwischen ihnen genau 90 Grad beträgt. Diese Eigenschaft ermöglicht es uns, die Orthogonalität von zwei Geraden zu überprüfen, indem wir den Winkel zwischen ihnen messen.
Eine weitere wichtige Eigenschaft ist, dass orthogonale Geraden in einer Ebene liegen. Dies bedeutet, dass sie sich nicht in unterschiedlichen Ebenen befinden können. Wenn zwei Geraden orthogonal zueinander sind, liegt dies daran, dass ihre Richtungsvektoren senkrecht aufeinander stehen. Dies ist ein weiteres Merkmal orthogonaler Geraden.
Bedeutung von orthogonalen Geraden:
Orthogonale Geraden haben in der Mathematik verschiedene Anwendungen und Bedeutungen. Sie werden häufig verwendet, um geometrische Probleme zu lösen und Beziehungen zwischen verschiedenen Elementen zu beschreiben.
In der Ebene können orthogonale Geraden beispielsweise dazu verwendet werden, rechtwinklige Dreiecke zu konstruieren oder die Lage von Punkten und Objekten zueinander zu bestimmen. Sie sind auch wichtig in der analytischen Geometrie, um Gleichungen von Geraden zu lösen oder deren Eigenschaften zu untersuchen.
Im dreidimensionalen Raum können orthogonale Geraden ebenfalls zur Lösung geometrischer Probleme verwendet werden. Sie spielen eine wichtige Rolle bei der Konstruktion von räumlichen Figuren und bei der Bestimmung von Schnittpunkten oder Abständen zwischen Objekten.
Die Bedeutung orthogonaler Geraden liegt also darin, dass sie uns helfen, Beziehungen zwischen verschiedenen Elementen in der Geometrie zu verstehen und mathematische Probleme zu lösen.
Orthogonalität in der Ebene und im Raum: Alle wichtigen Informationen
Orthogonalität ist ein Begriff, der sowohl in der Ebene als auch im Raum verwendet wird. Wenn zwei Geraden g und h orthogonal zueinander sind, bedeutet dies, dass sie sich im rechten Winkel (90°) schneiden. Diese senkrechte Beziehung zwischen den Geraden kann auch mit dem Symbol „⊥“ dargestellt werden.
Um die Orthogonalität von zwei Geraden zu überprüfen, muss man den Winkel zwischen ihnen messen und sicherstellen, dass er 90° beträgt. Im dreidimensionalen Raum kann dies jedoch schwieriger sein, da die Geraden in unterschiedlichen Ebenen liegen können. In diesem Fall verwendet man Vektoren, um die Richtung der Geraden darzustellen. Das Skalarprodukt der Richtungsvektoren von g und h wird berechnet, um festzustellen, ob sie orthogonal zueinander sind. Wenn das Skalarprodukt 0 ergibt, sind die Geraden orthogonal zueinander.
Auch Ebenen können orthogonal zueinander stehen oder von Geraden geschnitten werden. Um dies zu überprüfen, verwendet man Normalenvektoren. Zwei Ebenen sind senkrecht zueinander, wenn das Skalarprodukt ihrer Normalenvektoren 0 ergibt.
Orthogonale Geraden: Definition und Merkmale
Definition der orthogonalen Geraden:
Orthogonale Geraden sind zwei Geraden, die sich im rechten Winkel (90°) schneiden. Sie werden auch als senkrecht zueinander bezeichnet. Um die Orthogonalität von zwei Geraden zu überprüfen, misst man den Winkel zwischen ihnen und prüft, ob er 90° beträgt. Alternativ kann auch die Kurzschreibweise g ⊥ h verwendet werden, um auszudrücken, dass die Geraden g und h orthogonal zueinander sind.
Eigenschaften der orthogonalen Geraden:
– Orthogonale Geraden liegen in einer Ebene.
– Wenn eine Gerade g vorgegeben ist, kann man eine senkrecht dazu stehende Gerade h konstruieren.
– Im dreidimensionalen Raum können sich orthogonale Geraden ohne Schnittpunkt befinden, wenn sie in unterschiedlichen Ebenen liegen.
– Zur Darstellung von Geraden im dreidimensionalen Raum werden Vektoren verwendet. Das Skalarprodukt der Richtungsvektoren von g und h wird berechnet, um festzustellen, ob sie orthogonal zueinander sind. Wenn das Skalarprodukt 0 ergibt, sind die beiden Richtungsvektoren senkrecht aufeinander und somit sind g und h orthogonal zueinander.
– Die Orthogonalität ist eine Aussage über die Richtungen der Geraden und nicht über Schnittpunkte.
– Neben orthogonalen Geraden können auch Ebenen orthogonal zueinander stehen oder von geraden Linien geschnitten werden. Zur Überprüfung dieser Orthogonalität spielen Normalenvektoren eine wichtige Rolle. Sie können entweder direkt abgelesen oder mithilfe des Kreuzprodukts aus den Richtungsvektoren einer Ebene berechnet werden.
– Zwei Ebenen sind senkrecht zueinander, wenn das Skalarprodukt ihrer Normalenvektoren 0 ergibt.
Merke: Die Reihenfolge der Geraden ist egal. Wenn g orthogonal zu h ist (g ⊥ h), dann ist auch h orthogonal zu g (h ⊥ g). Eine Gerade steht genau dann orthogonal auf einer Ebene, wenn sie parallel zu deren Normalenvektor ist.
Wie überprüft man die Orthogonalität von Geraden?

Um die Orthogonalität von zwei Geraden zu überprüfen, musst du den Winkel zwischen ihnen messen. Wenn der Winkel 90º beträgt, sind die Geraden orthogonal zueinander. Du kannst auch die Kurzschreibweise „g ⊥ h“ verwenden, um auszudrücken, dass g orthogonal zu h ist.
Es gibt verschiedene Möglichkeiten, die Orthogonalität von Geraden zu überprüfen:
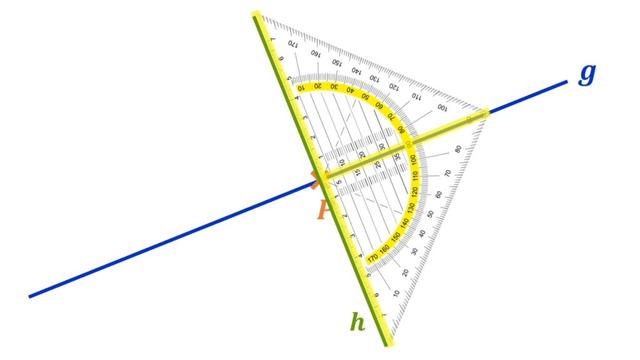
1. Messung des Winkels: Du kannst den Winkel zwischen den beiden Geraden mit einem Winkelmesser oder einem Geodreieck messen. Wenn der Winkel 90º beträgt, sind die Geraden orthogonal zueinander.
2. Skalarprodukt der Richtungsvektoren: Wenn du die Geradengleichungen hast, kannst du das Skalarprodukt ihrer Richtungsvektoren berechnen. Ergibt das Skalarprodukt 0, sind die Geraden orthogonal zueinander.
Achte jedoch darauf, dass im dreidimensionalen Raum zwei Geraden orthogonal zueinander sein können, ohne sich zu schneiden. Die Orthogonalität bezieht sich hier nur auf die Richtungen der Geraden und nicht auf Schnittpunkte.
Merke dir auch, dass eine Gerade genau dann orthogonal auf einer Ebene steht, wenn sie parallel zu deren Normalenvektor ist. Zwei Ebenen sind senkrecht zueinander, wenn das Skalarprodukt ihrer Normalenvektoren 0 ergibt.
Die Reihenfolge der Benennung der Geraden ist dabei egal. Wenn g orthogonal zu h ist (g ⊥ h), dann ist auch h orthogonal zu g (h ⊥ g).
Orthogonalität in der Mathematik: Eine umfassende Erklärung
Was bedeutet orthogonal?
Die Orthogonalität bezieht sich auf die Beziehung zwischen zwei Geraden oder Ebenen. Zwei Geraden g und h gelten als orthogonal zueinander, wenn sie sich im rechten Winkel (90°) schneiden. Man sagt auch, dass sie senkrecht zueinander stehen. Um die Orthogonalität zu überprüfen, misst man den Winkel zwischen den beiden Geraden und stellt sicher, dass er 90º beträgt. Alternativ kann man die Kurzschreibweise g ⊥ h verwenden.
Eigenschaften orthogonaler Geraden
Orthogonale Geraden haben besondere Eigenschaften. Wenn eine Gerade g vorgegeben ist und man eine Gerade h konstruieren möchte, die senkrecht dazu steht, gibt es bestimmte Vorgehensweisen dafür. Diese Methoden gelten jedoch nur für Geraden in einer Ebene, also im zweidimensionalen Raum.
Im dreidimensionalen Raum können Geraden auch orthogonal zueinander sein, ohne sich zu schneiden. In diesem Fall kann eine Gerade viel höher oder tiefer liegen als die andere. Die Orthogonalität bezieht sich hier nur auf die Richtungen der Richtungsvektoren der Geraden und nicht auf Schnittpunkte.
Orthogonalität von Ebenen
Auch Ebenen können orthogonal zueinander stehen oder von Geraden geschnitten werden. Zur Überprüfung der Orthogonalität spielen wieder Vektoren eine wichtige Rolle, insbesondere die sogenannten Normalenvektoren. Diese können direkt abgelesen oder mithilfe des Kreuzproduktes der Richtungsvektoren einer Ebene berechnet werden.
Zwei Ebenen gelten als senkrecht zueinander, wenn das Skalarprodukt ihrer Normalenvektoren 0 ergibt.
Merke dir also: Orthogonalität bezieht sich auf die Winkelbeziehung zwischen Geraden und die Richtungen von Vektoren, während sie für Ebenen durch das Skalarprodukt ihrer Normalenvektoren definiert wird.
Zusammenfassend kann gesagt werden, dass der Begriff „orthogonal“ in der Mathematik die Unabhängigkeit oder Senkrechtheit von Vektoren oder Funktionen beschreibt. Es ist ein wichtiger Begriff in linearen Algebra und Signalverarbeitung, der dazu dient, Beziehungen zwischen verschiedenen Größen zu analysieren und zu verstehen.

