Was ist achsensymmetrisch? – Bedeutung und Erkennung der Achsensymmetrie

Achsensymmetrie bezieht sich auf die Eigenschaft eines Objekts, dass es spiegelbildlich entlang einer Achse ist. In diesem Artikel werden wir die Bedeutung von Achsensymmetrie untersuchen und Beispiele aus verschiedenen Bereichen betrachten. Erfahren Sie, wie dieses Konzept in der Geometrie, Kunst und anderen Bereichen angewendet wird und warum es eine wichtige Rolle spielt.

Erklärung der Achsensymmetrie: Was bedeutet achsensymmetrisch?

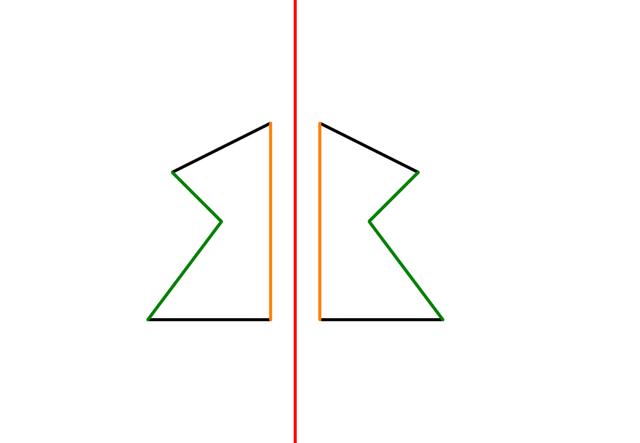
Die Achsensymmetrie ist ein Konzept, das sowohl in der Geometrie als auch in der Mathematik Anwendung findet. Eine Figur oder eine Funktion wird als achsensymmetrisch bezeichnet, wenn sie an einer Symmetrieachse gespiegelt werden kann und dabei die gespiegelte Hälfte genauso aussieht wie die erste Hälfte.

Eine Symmetrieachse, auch Spiegelachse genannt, ist einfach eine Linie, an der die Figur oder Funktion gespiegelt wird. Wenn man die Figur entlang dieser Linie faltet oder die Funktion entlang dieser Linie spiegelt, liegen beide Hälften deckungsgleich aufeinander.

In der Geometrie gibt es verschiedene Figuren, die achsensymmetrisch sein können. Ein Rechteck beispielsweise kann an zwei Symmetrieachsen gespiegelt werden. Ein Quadrat hat ebenfalls diese beiden Symmetrieachsen, aber zusätzlich auch noch beide Diagonalen als Spiegelachsen. Ein Trapez ist nur dann achsensymmetrisch, wenn es gleichschenklig ist. Ein gleichseitiges Dreieck besitzt drei Spiegelachsen, während ein gleichschenkliges Dreieck nur eine Symmetrieachse hat. Ein Kreis hingegen hat unendlich viele Symmetrieachsen, die alle durch den Mittelpunkt gehen.

Auch bei Funktionen kann man die Achsensymmetrie untersuchen. Dafür gibt es eine Formel zur Bestimmung der Achsensymmetrie zur y-Achse. Man vergleicht die Funktion f(-x) mit der Funktion f(x). Wenn beide Funktionen genau gleich sind, ist die Funktion achsensymmetrisch zur y-Achse. Ist dies nicht der Fall, ist die Funktion nicht zur y-Achse symmetrisch.

Die Achsensymmetrie wird auch als Spiegelsymmetrie bezeichnet, da man die Figur oder Funktion an einer Symmetrieachse spiegelt.

Neben der Achsensymmetrie gibt es noch die Punktsymmetrie. Dabei dreht man eine Figur oder eine Funktion um einen festen Punkt. Es ist wichtig, sowohl über die Achsensymmetrie als auch über die Punktsymmetrie Bescheid zu wissen.

Auf Studyflix bieten wir kostenlos hochwertige Bildungsinhalte an. Um dies zu ermöglichen, sind wir auf die Unterstützung unserer Werbepartner angewiesen. Wir bitten dich daher darum, deinen Adblocker für Studyflix auszuschalten oder uns zu den Ausnahmen hinzuzufügen. Dies hilft uns weiter und tut dir nicht weh. Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte lade anschließend die Seite neu.

Beispiel:

Um nachzuweisen, ob eine Funktion achsensymmetrisch zur y-Achse ist, vergleicht man f(-x) mit f(x). Wenn beide Funktionen genau gleich sind, ist die Funktion achsensymmetrisch zur y-Achse.

Achsensymmetrie erkennen: Wie erkennt man eine Achsensymmetrie?

Eine Achsensymmetrie bei einer Figur kann erkannt werden, indem man die Figur an einer Symmetrieachse spiegeln kann. Eine Symmetrieachse, auch Spiegelachse genannt, ist einfach die Linie, an der die Figur gespiegelt wird. Wenn das Bild entlang der Symmetrieachse gefaltet wird, liegen die Figuren deckungsgleich aufeinander.

Bei Funktionen kann die Achsensymmetrie mithilfe einer Achsensymmetrie-Formel ermittelt werden. Diese Formel gibt an, ob eine Funktion symmetrisch zur y-Achse ist. Dabei wird untersucht, ob f(-x) = f(x) gilt.

Um eine Achsensymmetrie bei einem Rechteck zu erkennen, kann es an genau zwei Symmetrieachsen gespiegelt werden. Ein Quadrat hat ebenfalls diese beiden Symmetrieachsen und zusätzlich beide Diagonalen als Spiegelachsen. Ein Trapez ist achsensymmetrisch mit einer Symmetrieachse, aber nur wenn es gleichschenklig ist. Ein gleichseitiges Dreieck ist achsensymmetrisch mit drei Spiegelachsen, während ein gleichschenkliges Dreieck nur eine Symmetrieachse hat. Ein Kreis hat unendlich viele Symmetrieachsen, die alle durch den Mittelpunkt gehen.

Grundsätzlich kann jede beliebige Figur achsensymmetrisch sein. Es gibt jedoch auch Figuren, die keine Achsensymmetrie aufweisen.

Auch bei Funktionen kann eine Achsensymmetrie zur y-Achse nachgewiesen werden. Eine Funktion ist achsensymmetrisch zur y-Achse, wenn f(-x) = f(x) gilt.

Die Achsensymmetrie wird auch als Spiegelsymmetrie bezeichnet, da die Figur oder Funktion an der Symmetrieachse gespiegelt wird und die gespiegelte Hälfte genauso aussieht wie die erste Hälfte.

Neben der Achsensymmetrie gibt es auch noch die Punktsymmetrie. Bei der Punktsymmetrie wird eine Figur oder Funktion um einen festen Punkt gedreht. Es ist wichtig, sowohl über die Achsensymmetrie als auch über die Punktsymmetrie Bescheid zu wissen.

Um hochwertige Bildung kostenlos anbieten zu können, benötigen wir Unterstützung von Werbepartnern. Wir bitten daher darum, den Adblocker für Studyflix auszuschalten oder uns zu den Ausnahmen hinzuzufügen. Eine kurze Anleitung dazu findest du hier.

Symmetrieachsen bei geometrischen Figuren: Welche Symmetrieachsen haben Rechtecke, Quadrate und Dreiecke?

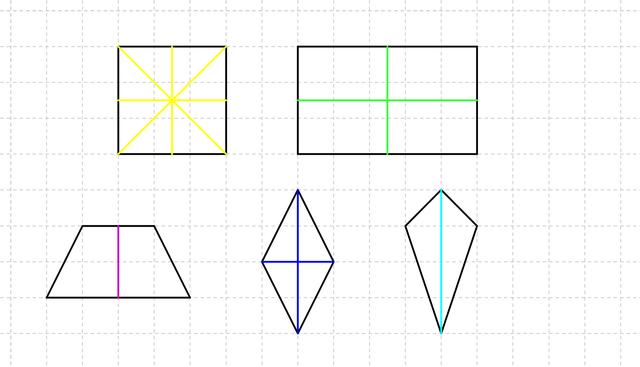
Rechtecke:

– Rechtecke haben zwei Symmetrieachsen. Diese verlaufen entlang der Mittellinien, die die gegenüberliegenden Seiten des Rechtecks verbinden.

Quadrate:

– Quadrate haben ebenfalls zwei Symmetrieachsen, die entlang der Mittellinien verlaufen und die gegenüberliegenden Seiten des Quadrats verbinden.
– Zusätzlich zu den beiden Symmetrieachsen haben Quadrate auch noch beide Diagonalen als Spiegelachsen.

Dreiecke:

– Gleichseitige Dreiecke sind achsensymmetrisch und haben drei Symmetrieachsen. Diese verlaufen entlang der Mittellinien, die jeweils eine Seite mit dem gegenüberliegenden Eckpunkt verbinden.
– Gleichschenklige Dreiecke haben dagegen nur eine Symmetrieachse, die entlang der Mittellinie verläuft, welche die beiden gleich langen Seiten miteinander verbindet.

Es ist wichtig anzumerken, dass diese Eigenschaften nur für spezifische Arten von Rechtecken, Quadraten und Dreiecken gelten. Andere Formen können unterschiedliche Anzahlen von Symmetrieachsen aufweisen oder möglicherweise gar keine Achsensymmetrie besitzen.

Symmetrieachsen bei einem Kreis: Wie viele Symmetrieachsen hat ein Kreis?

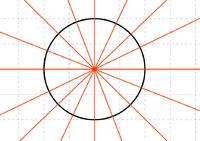
Ein Kreis hat unendlich viele Symmetrieachsen, die alle durch den Mittelpunkt des Kreises gehen. Das bedeutet, dass jede Linie, die durch den Mittelpunkt gezogen wird, eine Symmetrieachse des Kreises ist.

Diese Symmetrieachsen teilen den Kreis in zwei gleiche Hälften. Wenn man den Kreis entlang einer dieser Achsen spiegelt, liegen die beiden Hälften deckungsgleich aufeinander.

Da der Kreis rund ist und keine geraden Kanten hat, gibt es keine weiteren Symmetrieachsen außer denen, die durch den Mittelpunkt verlaufen.

Zusammenfassend kann man sagen, dass ein Kreis unendlich viele Symmetrieachsen hat, die alle durch den Mittelpunkt gehen.

Achsensymmetrie bei Funktionen: Wie kann man die Achsensymmetrie einer Funktion nachweisen?

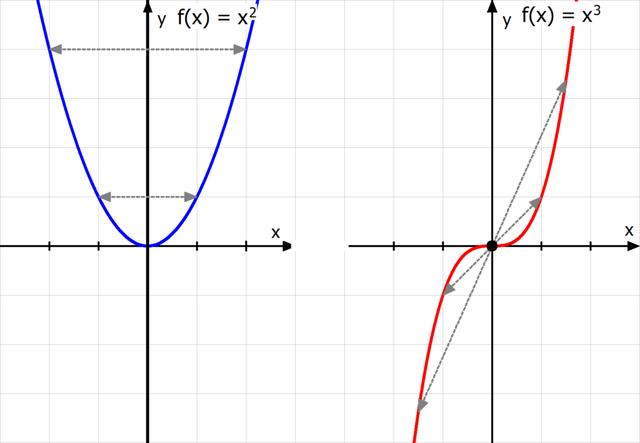
Was ist Achsensymmetrie bei Funktionen?

Achsensymmetrie bei Funktionen bedeutet, dass die Funktion symmetrisch zur y-Achse ist. Das heißt, wenn man die Funktion entlang der y-Achse spiegelt, sehen beide Hälften identisch aus. Um die Achsensymmetrie einer Funktion nachzuweisen, gibt es eine bestimmte Vorgehensweise.

Vorgehensweise zum Nachweis der Achsensymmetrie

1. Berechnung von f(-x): Ersetze in der gegebenen Funktion das x durch ein (-x). Dadurch erhältst du eine neue Funktion.
2. Vergleich von f(-x) und f(x): Überprüfe, ob die beiden Funktionen f(-x) und f(x) identisch sind. Wenn sie gleich sind, dann ist die Funktion achsensymmetrisch zur y-Achse.

Beispiel:
Angenommen wir haben die Funktion f(x) = x^2.
1. Berechnung von f(-x): Ersetze x durch (-x), also f(-x) = (-x)^2 = x^2.
2. Vergleich von f(-x) und f(x): Da f(-x) = x^2 und f(x) = x^2 identisch sind, ist die Funktion achsensymmetrisch zur y-Achse.

Diese Vorgehensweise ermöglicht es uns, schnell und einfach festzustellen, ob eine gegebene Funktion achsensymmetrisch zur y-Achse ist oder nicht.

Unterschied zwischen Achsensymmetrie und Punktsymmetrie: Was ist der Unterschied zwischen den beiden Symmetrietypen?

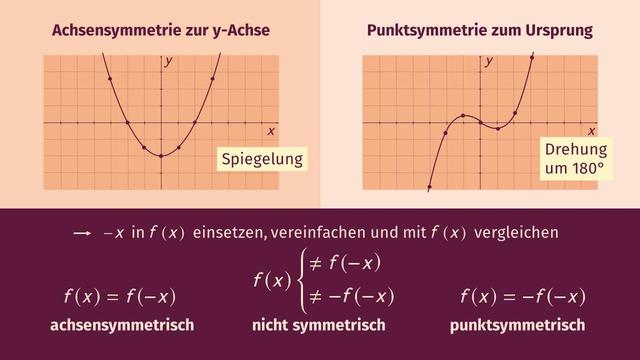
Achsensymmetrie

Die Achsensymmetrie, auch Spiegelsymmetrie genannt, tritt auf, wenn eine Figur oder Funktion an einer Symmetrieachse gespiegelt werden kann und die gespiegelte Hälfte genau gleich aussieht wie die erste Hälfte. Die Symmetrieachse ist dabei die Linie, an der die Figur oder Funktion gespiegelt wird. Bei Figuren können dies beispielsweise Diagonalen oder Seitenlängen sein, während bei Funktionen die Spiegelachse in der Regel die y-Achse ist.

Punktsymmetrie

Die Punktsymmetrie tritt auf, wenn eine Figur oder Funktion um einen festen Punkt gedreht werden kann und das Ergebnis genauso aussieht wie vorher. Dabei wird jede Punktposition mit ihrer Spiegelposition in Bezug auf den festen Punkt verbunden. Im Gegensatz zur Achsensymmetrie erfolgt hier keine Spiegelung entlang einer Linie.

Der Hauptunterschied zwischen Achsensymmetrie und Punktsymmetrie liegt also darin, dass bei der Achsensymmetrie eine Spiegelung entlang einer Linie stattfindet, während bei der Punktsymmetrie eine Drehung um einen festen Punkt erfolgt.

Zusammenfassend kann gesagt werden, dass eine Figur achsensymmetrisch ist, wenn sie eine Achse besitzt, die die Figur in zwei spiegelverkehrte Hälften teilt. Diese Symmetrie ist wichtig in der Mathematik und hat viele Anwendungen sowohl im Alltag als auch in anderen wissenschaftlichen Bereichen.