Wie verkürzt man Brüche? Lerne in diesem Artikel, wie du Brüche auf ihre einfachste Form reduzieren kannst. Wir werden die Grundlagen der Bruchrechnung erklären und dir einfache Schritte zeigen, um Brüche zu kürzen. Egal ob du Schüler oder Student bist, dieses Tutorial wird dir helfen, Brüche schnell und effizient zu vereinfachen. Verpasse nicht diese Gelegenheit, deine mathematischen Fähigkeiten zu verbessern!
Effektive Bruchrechnung: Wie man Brüche richtig kürzt

Warum ist das Kürzen von Brüchen wichtig?
Beim Rechnen mit Brüchen ist es oft erforderlich, die Brüche zu kürzen. Das bedeutet, dass der Bruch so vereinfacht wird, dass der Zähler und der Nenner keinen gemeinsamen Teiler mehr haben. Durch das Kürzen werden die Brüche übersichtlicher und leichter zu handhaben. Außerdem ermöglicht es das Kürzen, den kleinstmöglichen Ausdruck eines Bruchs zu finden.
Wie kürzt man einen Bruch?
Um einen Bruch zu kürzen, müssen wir den größten gemeinsamen Teiler (ggT) von Zähler und Nenner finden. Der ggT ist die größte Zahl, durch die sowohl der Zähler als auch der Nenner ohne Rest teilbar sind. Wenn wir den ggT gefunden haben, teilen wir sowohl den Zähler als auch den Nenner des Bruchs durch diese Zahl. Dadurch erhalten wir einen gekürzten Bruch.
Beispiel:
Wir wollen den Bruch 12/24 kürzen.
Der ggT von 12 und 24 ist 12.
Durch Division von Zähler und Nenner mit 12 erhalten wir den gekürzten Bruch 1/2.
Es ist wichtig zu beachten, dass ein gekürzter Bruch denselben Wert wie der Ursprungsbruch hat. Das Kürzen ändert nur die Darstellung des Bruchs, nicht jedoch seinen Wert.
Zusammenfassend lässt sich sagen, dass das Kürzen von Brüchen eine wichtige Technik in der Bruchrechnung ist, um Brüche übersichtlicher zu machen und den kleinstmöglichen Ausdruck eines Bruchs zu finden. Durch das Teilen des Zählers und des Nenners mit dem größten gemeinsamen Teiler wird der Bruch gekürzt, ohne seinen Wert zu verändern.
Schritt für Schritt: Das Kürzen von Brüchen leicht gemacht
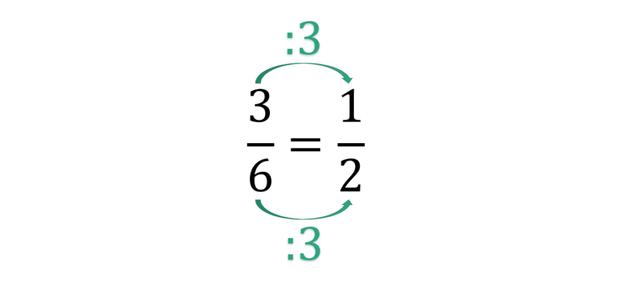
Grundlagen des Kürzens von Brüchen
Beim Kürzen von Brüchen geht es darum, den Bruch so weit wie möglich zu vereinfachen, indem man Zähler und Nenner durch eine gemeinsame Zahl teilt. Dadurch erhält man einen äquivalenten Bruch mit kleineren Zahlen. Um einen Bruch zu kürzen, sucht man nach dem größten gemeinsamen Teiler (ggT) von Zähler und Nenner und teilt beide durch diesen ggT.
Schritt-für-Schritt-Anleitung zum Kürzen von Brüchen
1. Schritt: Bestimme den ggT von Zähler und Nenner.
2. Schritt: Teile sowohl Zähler als auch Nenner durch den ggT.
3. Schritt: Überprüfe, ob der gekürzte Bruch bereits im einfachsten Ausdruck ist. Falls nicht, wiederhole die Schritte 1 und 2.
Beispiel:
Wir möchten den Bruch 12/24 kürzen.
1. Schritt: Der ggT von 12 und 24 ist 12.
2. Schritt: Teilen wir sowohl Zähler als auch Nenner durch 12, erhalten wir den gekürzten Bruch 1/2.
Das Kürzen von Brüchen ist eine wichtige Fähigkeit in der Mathematik und erleichtert das Rechnen mit Brüchen erheblich. Mit bettermarks können Schülerinnen und Schüler diese Fertigkeit auf interaktive Weise üben und ihr Verständnis vertiefen.
Praktische Tipps: So kürzt man Brüche einfach und schnell
1. Bestimme den größten gemeinsamen Teiler (ggT)
Um einen Bruch zu kürzen, musst du den größten gemeinsamen Teiler (ggT) von Zähler und Nenner finden. Der ggT ist die größte Zahl, die sowohl den Zähler als auch den Nenner ohne Rest teilt.
2. Teile Zähler und Nenner durch den ggT
Dividiere sowohl den Zähler als auch den Nenner des Bruchs durch den ggT. Dadurch erhältst du einen gekürzten Bruch, der denselben Wert wie der ursprüngliche Bruch hat.
Beispiel:
Angenommen, du hast den Bruch 12/18.
Der ggT von 12 und 18 ist 6.
Teile nun sowohl den Zähler als auch den Nenner durch 6:
12 ÷ 6 = 2
18 ÷ 6 = 3
Der gekürzte Bruch lautet also 2/3.
Weitere Tipps:
– Achte darauf, dass du immer so weit wie möglich kürzt. Wenn der ggT bereits 1 ist, kann der Bruch nicht weiter gekürzt werden.
– Wenn der Zähler größer als der Nenner ist, handelt es sich um einen unechten Bruch. In diesem Fall kannst du vor dem Kürzen eine Division durchführen, um zu sehen, wie oft der Nenner in den Zähler passt.
Mit diesen praktischen Tipps kannst du Brüche einfach und schnell kürzen. Viel Spaß beim Üben!
Bruchrechnung vereinfacht: Die Grundlagen des Kürzens von Brüchen
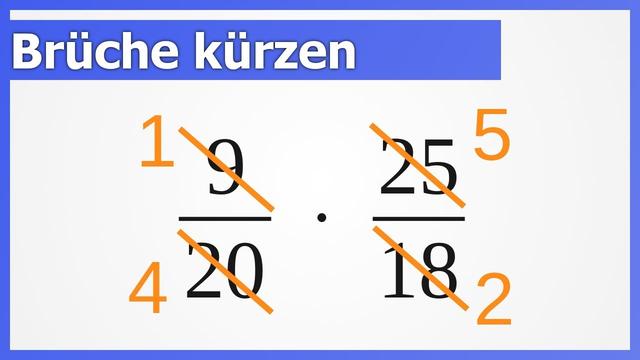
Was ist das Kürzen von Brüchen?
Beim Kürzen von Brüchen geht es darum, den Bruch so zu vereinfachen, dass der Zähler und der Nenner keinen gemeinsamen Teiler mehr haben. Dadurch wird der Bruch übersichtlicher und einfacher zu rechnen.
Wie funktioniert das Kürzen von Brüchen?
Um einen Bruch zu kürzen, sucht man nach dem größten gemeinsamen Teiler (ggT) von Zähler und Nenner. Dieser ggT wird dann sowohl im Zähler als auch im Nenner gekürzt. Das bedeutet, dass man beide Zahlen durch den ggT teilt.
Beispiel:
Angenommen wir haben den Bruch 8/12. Der ggT von 8 und 12 ist 4. Durch Teilen beider Zahlen durch 4 erhalten wir den gekürzten Bruch 2/3.
Es ist wichtig zu beachten, dass ein gekürzter Bruch denselben Wert wie der Ausgangsbruch hat. Das heißt, 8/12 ist gleichwertig zu 2/3.
Das Kürzen von Brüchen erleichtert nicht nur das Rechnen mit ihnen, sondern ermöglicht auch einen besseren Überblick über die mathematischen Zusammenhänge.
Erfolgreiches Lernen: Strategien zum Kürzen von Brüchen
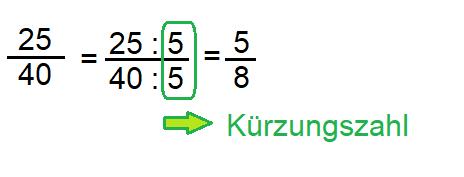
1. Was ist das Kürzen von Brüchen?
Das Kürzen von Brüchen ist eine wichtige Fähigkeit in der Mathematik, die es ermöglicht, Brüche auf ihren kleinstmöglichen Wert zu reduzieren. Dabei werden sowohl der Zähler als auch der Nenner des Bruchs durch einen gemeinsamen Teiler geteilt. Das Ergebnis ist ein gekürzter Bruch, bei dem keine weiteren ganzzahligen Teiler mehr möglich sind.
2. Strategien zum Kürzen von Brüchen
Es gibt verschiedene Strategien, um Brüche zu kürzen. Eine Möglichkeit besteht darin, den größten gemeinsamen Teiler (ggT) des Zählers und des Nenners zu bestimmen und beide durch diesen zu teilen. Eine andere Methode ist das Prüfen der einzelnen Primfaktoren des Zählers und des Nenners, um mögliche gemeinsame Faktoren zu finden und diese zu kürzen.
– Beispiel 1: Betrachten wir den Bruch 12/24. Der ggT von 12 und 24 ist 12. Wenn wir sowohl den Zähler als auch den Nenner durch 12 teilen, erhalten wir den gekürzten Bruch 1/2.
– Beispiel 2: Nehmen wir den Bruch 16/20. Die Primfaktoren von 16 sind 2^4 und die Primfaktoren von 20 sind 2^2 * 5. Der gemeinsame Faktor ist also 2^2 = 4. Durch Teilen von Zähler und Nenner durch 4 erhalten wir den gekürzten Bruch 4/5.
Es ist wichtig, dass Schülerinnen und Schüler diese Strategien üben und verstehen, um erfolgreich Brüche kürzen zu können. Durch regelmäßiges Üben mit adaptiven Übungen wie bettermarks können sie ihre Fähigkeiten verbessern und ein besseres Verständnis für die Grundlagen der Bruchrechnung entwickeln.
3. Vorteile des Kürzens von Brüchen
Das Kürzen von Brüchen hat mehrere Vorteile. Erstens ermöglicht es eine einfachere Darstellung von Brüchen, da sie auf ihren kleinstmöglichen Wert reduziert werden. Dadurch wird das Rechnen mit Brüchen insgesamt einfacher und übersichtlicher. Zweitens erleichtert das Kürzen auch das Vergleichen von Brüchen, da man schnell erkennen kann, welcher Bruch größer oder kleiner ist. Drittens kann das Kürzen von Brüchen auch dabei helfen, reale Situationen besser zu verstehen, indem man zum Beispiel Mengenverhältnisse anschaulicher darstellen kann.
Insgesamt ist das Kürzen von Brüchen eine wichtige Fähigkeit in der Mathematik, die Schülerinnen und Schülern dabei hilft, ein solides Fundament in der Bruchrechnung aufzubauen und erfolgreich mit mathematischen Aufgaben umzugehen.
Optimiere deine Mathematikkenntnisse: Die Kunst des Bruchkürzens
Warum ist das Kürzen von Brüchen wichtig?
Das Kürzen von Brüchen ist eine grundlegende Fähigkeit in der Mathematik, die es uns ermöglicht, Brüche auf ihre einfachste Form zu reduzieren. Durch das Kürzen können wir den Nenner und Zähler eines Bruchs teilen, indem wir gemeinsame Teiler finden und diese herauskürzen. Dies hilft uns, Brüche übersichtlicher und einfacher zu handhaben.
Wie funktioniert das Kürzen von Brüchen?
Um einen Bruch zu kürzen, müssen wir zunächst den größten gemeinsamen Teiler (ggT) von Zähler und Nenner finden. Der ggT ist die größte Zahl, die beide Zahlen ohne Rest teilt. Sobald wir den ggT gefunden haben, teilen wir sowohl Zähler als auch Nenner des Bruchs durch diesen Wert. Dadurch wird der Bruch auf seine einfachste Form reduziert.
Beispiel:
Angenommen, wir haben den Bruch 8/12. Um diesen zu kürzen, suchen wir den ggT von 8 und 12, der in diesem Fall 4 ist. Wir teilen sowohl den Zähler als auch den Nenner durch 4 und erhalten den gekürzten Bruch 2/3.
Vorteile des Kürzens von Brüchen
Das Kürzen von Brüchen hat mehrere Vorteile. Erstens macht es die Rechnung mit Brüchen einfacher und übersichtlicher. Indem wir Brüche auf ihre einfachste Form reduzieren, können wir sie besser vergleichen und addieren oder subtrahieren. Zweitens hilft uns das Kürzen, Brüche in alltäglichen Situationen besser zu verstehen. Wenn wir beispielsweise einen Kuchen in gleiche Stücke teilen möchten, ist es einfacher zu verstehen, dass 2 von 3 Stücken gegessen wurden als 8 von 12 Stücken.
Insgesamt ist das Kürzen von Brüchen eine wichtige Fähigkeit, die uns dabei hilft, Mathematik besser zu verstehen und anzuwenden. Durch die Nutzung von adaptiven Übungen wie bettermarks können Schülerinnen und Schüler ihre Kenntnisse im Kürzen von Brüchen verbessern und dadurch ihren Lernzuwachs steigern.
Insgesamt betrachtet ist das Kürzen von Brüchen eine wichtige mathematische Fähigkeit, die es ermöglicht, sie in einfacherer und übersichtlicher Form darzustellen. Durch das Teilen von Zähler und Nenner mit dem größten gemeinsamen Teiler kann der Bruch auf seinen kleinstmöglichen Ausdruck gebracht werden. Dies erleichtert nicht nur Rechenoperationen, sondern verbessert auch das Verständnis für mathematische Konzepte. Das Kürzen von Brüchen sollte daher regelmäßig geübt werden, um diese grundlegende Technik zu beherrschen.

