Eine Dezimalzahl ist eine Zahl, die nach dem Zehnersystem aufgebaut ist und durch ein Komma in einen ganzzahligen und einen dezimalen Teil gegliedert wird. Sie ermöglicht die Darstellung von Bruchteilen und rationalen Zahlen auf einfache Art und Weise. Dezimalzahlen werden im Alltag, in der Mathematik und in vielen anderen Bereichen verwendet, um Präzision und Genauigkeit zu gewährleisten. Erfahren Sie hier mehr über die Eigenschaften und Anwendungsbereiche von Dezimalzahlen.
Eigenschaften von Dezimalzahlen: Abbruch, Periode und Irrationalität
Eine Dezimalzahl kann verschiedene Eigenschaften haben, die sich auf ihre Nachkommastellen beziehen. Es gibt abbrechende Dezimalzahlen, bei denen die Reihe der Nachkommastellen endlich ist und keine weiteren von Null verschiedenen Zahlen folgen. Bei diesen Dezimalzahlen bricht die Reihe also ab.
Im Gegensatz dazu gibt es periodische Dezimalzahlen, bei denen sich ab einer bestimmten Stelle eine Ziffernfolge immer wiederholt. Diese wiederkehrende Ziffernfolge nennt man Periode. Die Reihe der Nachkommastellen bricht also nicht ab.
Eine weitere Art von Dezimalzahlen sind die irrationalen Zahlen. Bei diesen bricht die Reihe der Nachkommastellen ebenfalls nicht ab, jedoch gibt es hier keine Periode. Das bedeutet, dass keine Ziffernfolge immer wieder auftritt. Irrationale Zahlen sind deshalb nicht abbrechende und nicht periodische Dezimalzahlen.
Ein bekanntes Beispiel für eine irrationale Zahl ist die Zahl π (Pi). Sie lässt sich nicht als Bruch darstellen und hat unendlich viele Nachkommastellen ohne Periodizität.
Es ist wichtig zu beachten, dass beim Runden und Ordnen von Dezimalzahlen unterschiedliche Regeln gelten können. Beim Runden wird eine Dezimalzahl auf eine bestimmte Anzahl von Nachkommastellen gekürzt oder erweitert, um das Ergebnis mit einer gewünschten Genauigkeit anzugeben. Beim Ordnen werden Dezimalzahlen nach ihrer Größe auf einem Zahlenstrahl angeordnet.
Beim Runden einer Dezimalzahl gibt es verschiedene Verfahren, wie das Aufrunden oder Abrunden. Dabei wird die nächste Zehnerpotenz verwendet, um die Dezimalzahl auf die gewünschte Anzahl von Nachkommastellen zu runden.
Beim Ordnen von Dezimalzahlen auf einem Zahlenstrahl ist es hilfreich, die Stellenschreibweise der Dezimalzahlen zu kennen. Dabei werden die Zahlen nach ihrer Position im Zahlensystem geordnet, wobei die Nachkommastellen eine Rolle spielen.
Das Runden und Ordnen von Dezimalzahlen ist wichtig in vielen Alltagssituationen, zum Beispiel beim Bezahlen im Supermarkt oder bei komplexeren mathematischen Aufgaben. Es ermöglicht uns, Ergebnisse mit einer bestimmten Genauigkeit anzugeben und Dezimalzahlen zu vergleichen.
Genauigkeit und Rundung von Dezimalzahlen im Alltag
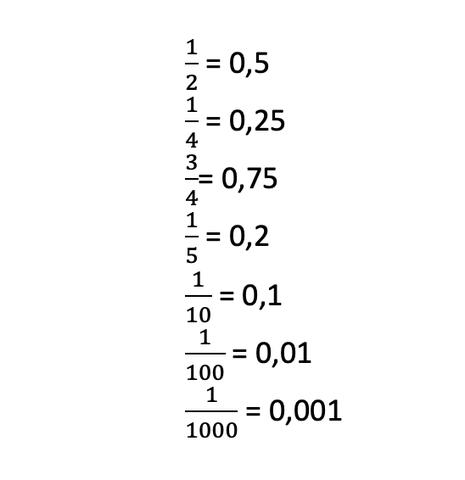
Die Genauigkeit und Rundung von Dezimalzahlen spielt eine wichtige Rolle im Alltag, insbesondere wenn es um Geldbeträge oder Messungen geht. In vielen Situationen ist es nicht notwendig oder sinnvoll, das Ergebnis mit voller Genauigkeit anzugeben.
Beispielsweise beim Einkaufen an der Supermarktkasse werden oft Eurobeträge mit zwei Nachkommastellen verlangt. Diese beiden Stellen repräsentieren die Centbeträge, die tatsächlich in physischer Form ausgegeben werden können. Alle weiteren Nachkommastellen sind für diesen Zweck irrelevant.
Um solche Fälle zu berücksichtigen, verwenden wir das Runden von Dezimalzahlen. Beim Runden wird eine Dezimalzahl auf eine bestimmte Anzahl von Nachkommastellen oder auf eine ganze Zahl gerundet. Dabei gibt es verschiedene Rundungsverfahren wie das Aufrunden oder Abrunden.
Bei der Verwendung von Dezimalzahlen in praktischen Situationen ist auch das Ordnen der Zahlen wichtig. Durch das Ordnen können wir beispielsweise Gewichte vergleichen oder den zeitlichen Ablauf von Ereignissen darstellen.
Ein hilfreiches Werkzeug beim Ordnen von Dezimalzahlen ist der Zahlenstrahl. Auf dem Zahlenstrahl werden die Dezimalzahlen entsprechend ihrer Größe angeordnet. Dies ermöglicht einen schnellen Vergleich und ein besseres Verständnis der Relationen zwischen den Zahlen.
Zusammenfassend ist es beim Umgang mit Dezimalzahlen im Alltag wichtig, die Genauigkeit zu beachten und die Zahlen gegebenenfalls zu runden. Das Ordnen von Dezimalzahlen erleichtert das Vergleichen und Verstehen der Zahlen. Der Einsatz von Werkzeugen wie dem Zahlenstrahl kann dabei hilfreich sein.
Dezimalzahlen: Anwendungsbereiche und Umwandlung in Brüche
Anwendungsbereiche von Dezimalzahlen
Dezimalzahlen finden in vielen Bereichen des Alltags Anwendung. Zum Beispiel werden Geldbeträge oft in Dezimalzahlen angegeben, um Centbeträge genau darstellen zu können. Auch bei Gewichten und Längen werden Dezimalzahlen verwendet, um präzise Messungen durchführen zu können. Darüber hinaus werden Dezimalzahlen in der Mathematik häufig für Berechnungen verwendet, da viele Ergebnisse nicht als glatte Zahlen angegeben werden können.
Umwandlung von Dezimalzahlen in Brüche
In einigen Fällen ist es sinnvoll, eine Dezimalzahl in einen Bruch umzuwandeln. Dies kann zum Beispiel dann der Fall sein, wenn man eine genaue Darstellung einer Zahl benötigt oder wenn man mit Brüchen einfacher rechnen kann. Um eine Dezimalzahl in einen Bruch umzuwandeln, muss man die Nachkommastelle als Bruchteil des Ganzen interpretieren.
Beispiel: Die Dezimalzahl 0,75 kann als Bruch dargestellt werden als 75/100 oder vereinfacht als 3/4.
Um eine Dezimalzahl mit einer endlichen Anzahl an Nachkommastellen (abbrechende Dezimalzahl) in einen Bruch umzuwandeln, wird der Nenner des Bruchs durch 10 hoch die Anzahl der Nachkommastellen bestimmt.
Beispiel: Die Dezimalzahl 0,6 kann als Bruch dargestellt werden als 6/10 oder vereinfacht als 3/5.
Bei Dezimalzahlen mit einer periodischen Nachkommastelle (periodische Dezimalzahl) wird der Nenner des Bruchs durch eine Zahl bestimmt, die so viele Neuner enthält wie es Perioden gibt, gefolgt von Nullen.
Beispiel: Die Dezimalzahl 0,333… kann als Bruch dargestellt werden als 1/3.
Es ist wichtig zu beachten, dass nicht alle Dezimalzahlen in Brüche umgewandelt werden können. Dies gilt insbesondere für irrationalen Zahlen wie \(\pi\) oder Wurzel aus 2. Diese Zahlen haben unendlich viele Nachkommastellen, die weder abbrechen noch periodisch sind. Daher können sie nicht genau als Bruch dargestellt werden.
Rechnen mit Dezimalzahlen: Addition, Subtraktion, Multiplikation und Division
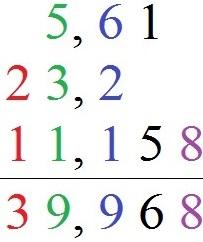
Beim Runden von Dezimalzahlen ist es wichtig, die gewünschte Genauigkeit zu beachten. Je nach Anwendungsbereich kann es sinnvoll sein, eine Dezimalzahl auf eine bestimmte Anzahl von Nachkommastellen zu runden. Dies wird oft gemacht, um das Ergebnis übersichtlicher darzustellen oder um mit Geldbeträgen zu arbeiten.
Beim Runden gibt es verschiedene Verfahren. Eine gängige Methode ist das „kaufmännische Runden“, bei dem ab der fünften Nachkommastelle auf- oder abgerundet wird, je nachdem ob die sechste Nachkommastelle größer oder kleiner als 5 ist. Wenn die sechste Nachkommastelle genau 5 ist, wird auf die nächste gerade Zahl gerundet.
Beim Ordnen von Dezimalzahlen geht es darum, sie in einer bestimmten Reihenfolge anzuordnen. Dies kann zum Beispiel beim Vergleichen von Größen oder beim Sortieren von Zahlen erforderlich sein.
Um Dezimalzahlen zu addieren und zu subtrahieren, werden sie zunächst so angeordnet, dass das Komma untereinander steht. Dann werden die Zahlen wie gewohnt addiert oder subtrahiert und das Komma im Ergebnis entsprechend platziert.
Bei der Multiplikation von Dezimalzahlen wird das Komma zunächst ignoriert und die Zahlen wie gewohnt multipliziert. Anschließend wird das Komma im Ergebnis so platziert, dass die Anzahl der Nachkommastellen stimmt.
Bei der Division von Dezimalzahlen wird ähnlich vorgegangen wie bei der Multiplikation. Das Komma wird zunächst ignoriert und die Zahlen wie gewohnt dividiert. Anschließend wird das Komma im Ergebnis so platziert, dass die Anzahl der Nachkommastellen stimmt.
Es ist wichtig, bei allen Rechenoperationen mit Dezimalzahlen auf die Stellenschreibweise zu achten und die richtige Anzahl von Nachkommastellen zu verwenden. Durch das Überschlagen oder Abschätzen der Ergebnisse kann man zudem überprüfen, ob das Ergebnis plausibel ist.
Runden von Dezimalzahlen: Regeln und Anwendungsbeispiele
Regeln für das Runden von Dezimalzahlen
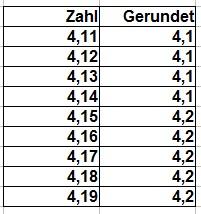
Beim Runden von Dezimalzahlen gibt es bestimmte Regeln, die beachtet werden sollten. Die wichtigste Regel besagt, dass bei einer 5 als letzter Ziffer der zu rundenden Zahl immer auf- oder abgerundet wird, je nachdem ob die vorherige Ziffer gerade oder ungerade ist. Ist die vorherige Ziffer gerade, wird abgerundet, ist sie ungerade, wird aufgerundet.
Ein Beispiel: Wenn wir die Zahl 3,45 auf eine Nachkommastelle runden wollen und die nächste Ziffer eine 5 ist, schauen wir uns die vorherige Ziffer an. In diesem Fall ist es eine 4, also eine gerade Zahl. Daher wird abgerundet und die gerundete Zahl lautet 3,4.
Anwendungsbeispiele für das Runden von Dezimalzahlen
Das Runden von Dezimalzahlen hat viele Anwendungsgebiete im Alltag. Hier sind einige Beispiele:
1. Geldbeträge: Wenn du zum Beispiel im Supermarkt einkaufst und deine Einkäufe bezahlst, möchtest du oft den genauen Betrag angeben. In diesem Fall rundest du den Gesamtbetrag auf zwei Nachkommastellen, da Centbeträge nicht weiter unterteilt werden können.
2. Längenangaben: Bei der Angabe von Längen kann es sinnvoll sein, auf eine bestimmte Genauigkeit zu runden. Zum Beispiel könntest du bei der Messung einer Strecke auf zwei Dezimalstellen runden, um eine genauere Angabe zu erhalten.
3. Zeitangaben: Bei der Umrechnung von Stunden in Minuten oder Sekunden kann das Runden von Dezimalzahlen nützlich sein. Hierbei kannst du auf die nächste ganze Zahl aufrunden, um eine übersichtlichere Zeitangabe zu erhalten.
Es ist wichtig zu beachten, dass das Runden von Dezimalzahlen immer eine gewisse Ungenauigkeit mit sich bringt. Je nach Anwendungsgebiet und gewünschter Genauigkeit sollten daher die Rundungsregeln entsprechend angewendet werden.
Ordnung von Dezimalzahlen auf dem Zahlenstrahl: Stellenschreibweise und Überschlag
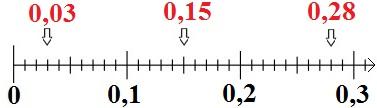
Die Ordnung von Dezimalzahlen auf dem Zahlenstrahl ist eine wichtige Methode, um Dezimalzahlen zu vergleichen und zu ordnen. Dabei wird die Stellenschreibweise verwendet, um die Position einer Dezimalzahl auf dem Zahlenstrahl darzustellen.
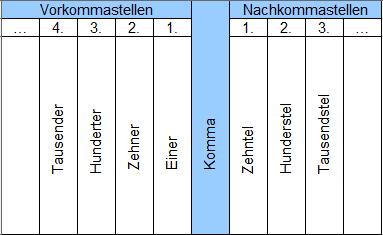
Die Stellenschreibweise besteht aus verschiedenen Stellenwerten, die von links nach rechts abnehmen. Die erste Stelle rechts vom Komma ist der Zehntelplatz, gefolgt vom Hundertstelplatz, Tausendstelplatz usw. Je weiter links eine Ziffer steht, desto größer ist ihr Stellenwert.
Um Dezimalzahlen auf dem Zahlenstrahl zu ordnen, kannst du den Überschlag verwenden. Dabei rundest du die Dezimalzahl auf den nächsten ganzzahligen Wert und vergleichst diese gerundete Zahl mit anderen Dezimalzahlen.
Beispiel:
1) Du möchtest die Dezimalzahlen 0,75 und 0,8 auf dem Zahlenstrahl ordnen.
– Runde 0,75 auf den nächsten ganzzahligen Wert: 1
– Runde 0,8 auf den nächsten ganzzahligen Wert: 1
Da beide gerundeten Zahlen gleich sind, musst du genauer betrachten.
– Die Dezimalzahl 0,75 liegt näher am Nullpunkt als die Dezimalzahl 0,8.
Also kannst du die Reihenfolge als 0,75 < 0,8 festlegen.
2) Du möchtest die Dezimalzahlen 2,3 und 2,35 auf dem Zahlenstrahl ordnen.
– Runde 2,3 auf den nächsten ganzzahligen Wert: 2
– Runde 2,35 auf den nächsten ganzzahligen Wert: 2
Da beide gerundeten Zahlen gleich sind, musst du genauer betrachten.
– Die Dezimalzahl 2,35 liegt näher am Nullpunkt als die Dezimalzahl 2,3.
Also kannst du die Reihenfolge als 2,35 < 2,3 festlegen.
Der Überschlag ermöglicht es dir also, Dezimalzahlen schnell und einfach auf dem Zahlenstrahl zu ordnen. Du kannst diese Methode verwenden, um verschiedene Dezimalzahlen zu vergleichen und ihre Positionen auf dem Zahlenstrahl zu bestimmen.
In der Mathematik bezieht sich eine Dezimalzahl auf eine Zahl, die in einem Zehnersystem dargestellt wird. Sie besteht aus einer ganzen Zahl und einem Bruchteil, der durch einen Dezimalpunkt getrennt ist. Dezimalzahlen sind wichtig für Berechnungen und Messungen in vielen Bereichen des täglichen Lebens. Das Verständnis von Dezimalzahlen ist daher unerlässlich, um mathematische Aufgaben erfolgreich zu lösen.