Was ist ein Dreisatz und wie funktioniert er?

Der Dreisatz ist eine mathematische Methode zur Lösung von proportionalen Verhältnissen. Mit Hilfe dieses einfachen Rechenverfahrens können unbekannte Größen in Bezug zueinander bestimmt werden. In diesem Artikel erfahren Sie, was ein Dreisatz ist und wie er angewendet wird.

Der Dreisatz: Ein wichtiges Lösungsverfahren in der Mathematik

Der Dreisatz ist ein grundlegendes Lösungsverfahren in der Mathematik, das uns hilft, Aufgaben zu lösen, bei denen zwei Größen proportional oder antiproportional zueinander stehen. Der Name „Dreisatz“ leitet sich von den drei Rechenschritten ab, die benötigt werden, um das Ergebnis zu berechnen.

Beim Dreisatz wird einer bestimmten Menge oder Größe eine weitere Menge oder Größe zugeordnet. Wenn sich die beiden Größen proportional verhalten, bedeutet dies, dass sie im gleichen Verhältnis zueinander stehen. Zum Beispiel gilt: Je mehr Fleisch ich kaufe, desto mehr muss ich bezahlen.

Im umgekehrten Dreisatz hingegen steht eine Menge oder Größe in einem antiproportionalen Verhältnis zu einer anderen. Das bedeutet, dass sich die beiden Größen umgekehrt proportional verhalten. Zum Beispiel gilt: Je mehr Bagger arbeiten, desto weniger Arbeitszeit wird benötigt.

Es ist wichtig, sorgfältig zu lesen und zu entscheiden, ob es sich bei einer Aufgabe um einen proportionalen oder antiproportionalen Zusammenhang handelt. Manchmal kann es auch vorkommen, dass eine Zuordnung weder proportional noch antiproportional ist.

Es gibt verschiedene Methoden und Schreibweisen zur Lösung von Aufgaben mit dem Dreisatz. Eine häufig verwendete Methode ist die Erstellung einer Tabelle mit zwei Spalten für die beiden Größen. Durch geschicktes Umrechnen und Multiplizieren können wir dann das gesuchte Ergebnis ermitteln.

Es ist auch möglich, Aufgaben mit Hilfe von Bruchgleichungen zu lösen. Dabei werden die beiden Größen in Form von Brüchen dargestellt und entsprechend umgeformt.

Um zu überprüfen, ob es sich tatsächlich um eine proportionale oder antiproportionale Zuordnung handelt, kann die Quotientengleichheit oder Produktgleichheit verwendet werden. Dabei werden zeilenweise die Quotienten oder Produkte gebildet und verglichen.

Der Dreisatz ist ein vielseitiges Lösungsverfahren, das uns dabei hilft, verschiedene mathematische Aufgaben zu lösen. Es ist wichtig, die verschiedenen Methoden und Schreibweisen zu kennen und anzuwenden, um die bestmögliche Lösung zu finden.

Proportionale und antiproportionale Zuordnung: Der Dreisatz erklärt

Der Dreisatz ist ein wichtiges Lösungsverfahren in der Mathematik, mit dem wir Aufgaben lösen können, bei denen zwei Größen proportional oder antiproportional zueinander stehen.

Eine proportionale Zuordnung liegt vor, wenn sich die beiden Größen in einem direkten Verhältnis zueinander verhalten. Das bedeutet, dass sie in gleichem Maße zunehmen oder abnehmen. Ein Beispiel dafür ist der Zusammenhang zwischen der Menge an Fleisch und dem Preis pro Kilogramm. Je mehr Fleisch gekauft wird, desto höher ist der Preis.

Bei einer antiproportionalen Zuordnung hingegen verhalten sich die beiden Größen umgekehrt proportional zueinander. Das bedeutet, dass sie sich entgegengesetzt verhalten. Ein Beispiel dafür ist der Zusammenhang zwischen der Anzahl an Baggern und der benötigten Arbeitszeit. Je mehr Bagger arbeiten, desto weniger Zeit wird benötigt.

Es ist wichtig, genau zu lesen und zu erkennen, ob es sich um einen proportionalen oder antiproportionalen Zusammenhang handelt. Manchmal kann es aber auch vorkommen, dass keine eindeutige Zuordnung besteht.

Der Dreisatz ermöglicht es uns, solche Aufgaben zu lösen. Es gibt verschiedene Methoden und Schreibweisen für den Dreisatz, man kann zum Beispiel eine Tabelle verwenden oder Bruchgleichungen aufstellen.

Um zu überprüfen, ob eine Zuordnung wirklich proportional oder antiproportional ist, kann man die Quotientengleichheit bzw. Produktgleichheit nutzen. Dabei werden die Quotienten bzw. Produkte der jeweiligen Größen berechnet und verglichen.

Der Dreisatz ist also ein nützliches Werkzeug, um proportionale und antiproportionale Zuordnungen zu lösen und zu überprüfen. Es ist wichtig, die Aufgaben genau zu lesen und den richtigen Lösungsweg auszuwählen.

Anwendung des Dreisatzes: Proportional oder antiproportional?

Der Dreisatz ist ein wichtiges Lösungsverfahren in der Mathematik, mit dem wir Aufgaben lösen können, bei denen zwei Größen proportional oder antiproportional zueinander stehen. Bei einer proportionalen Zuordnung gilt: Je mehr von einer Größe vorhanden ist, desto mehr von der anderen Größe gibt es. Bei einer antiproportionalen Zuordnung hingegen gilt: Je mehr von einer Größe vorhanden ist, desto weniger von der anderen Größe gibt es.

Beim Dreisatz werden einer bestimmten Menge oder Größe eine weitere Menge oder Größe zugeordnet. Wenn diese Zuordnung proportional ist, bedeutet das, dass sich die beiden Größen im gleichen Verhältnis ändern. Wenn die Zuordnung antiproportional ist, bedeutet das, dass sich die beiden Größen im umgekehrten Verhältnis ändern.

Es ist wichtig, die Aufgaben zum Dreisatz sorgfältig zu lesen und zu entscheiden, ob es sich um einen proportionalen oder antiproportionalen Zusammenhang handelt. Manchmal kann es auch vorkommen, dass keine eindeutige Zuordnung vorliegt und weder proportional noch antiproportional ist.

Um solche Aufgaben zu lösen, gibt es verschiedene Methoden wie den Einsatz einer Tabelle oder einer Bruchgleichung. Es spielt keine Rolle welche Methode gewählt wird, solange das Ergebnis korrekt berechnet wird.

Es ist auch möglich, die Richtigkeit der Zuordnung zu überprüfen. Bei proportionalen Zuordnungen kann die Quotientengleichheit verwendet werden, bei antiproportionalen Zuordnungen die Produktgleichheit.

Es ist wichtig zu beachten, dass bei antiproportionalen Zuordnungen auf der gegenüberliegenden Seite immer mit dem Gegenteil gerechnet werden muss. Je mehr von einer Größe vorhanden ist, desto weniger von der anderen Größe gibt es.

Der Dreisatz ist ein nützliches Werkzeug in der Mathematik, um proportionalen und antiproportionalen Zusammenhängen auf den Grund zu gehen und Aufgaben zu lösen. Es ist jedoch wichtig, die Aufgaben genau zu lesen und das richtige Lösungsverfahren anzuwenden.

Der Dreisatz: Lösen von Aufgaben zu proportionalen Zuordnungen

Der Dreisatz ist ein wichtiges Lösungsverfahren in der Mathematik, das verwendet wird, um Aufgaben zu lösen, bei denen zwei Größen proportional oder antiproportional zueinander stehen. Mit dem Dreisatz kann man zum Beispiel berechnen, wie viel man für eine bestimmte Menge Fleisch bezahlen muss oder wie lange man für eine bestimmte Strecke braucht.

Proportionale Zuordnungen liegen vor, wenn sich die beiden Größen direkt miteinander verändern. Das bedeutet, je mehr von einer Größe vorhanden ist, desto mehr von der anderen Größe gibt es auch. Ein Beispiel dafür ist der Zusammenhang zwischen der Menge an Fleisch und dem Preis pro Kilogramm. Je mehr Fleisch man kauft, desto höher ist der Preis.

Antiproportionale Zuordnungen hingegen liegen vor, wenn sich die beiden Größen indirekt miteinander verändern. Das bedeutet, je mehr von einer Größe vorhanden ist, desto weniger von der anderen Größe gibt es. Ein Beispiel dafür ist der Zusammenhang zwischen der Anzahl an Baggern und der benötigten Arbeitszeit. Je mehr Bagger arbeiten, desto weniger Zeit wird benötigt.

Es ist wichtig, bei Aufgaben zum Dreisatz genau zu lesen und zu entscheiden, ob es sich um einen proportionalen oder antiproportionalen Zusammenhang handelt. Manchmal kann es jedoch auch vorkommen, dass keine eindeutige Zuordnung besteht und weder proportional noch antiproportional gerechnet werden kann.

Es gibt verschiedene Methoden und Schreibweisen, um Aufgaben zum Dreisatz zu lösen. Eine häufig verwendete Methode ist die Tabelle mit zwei Spalten, in der die bekannten Werte eingetragen werden. Durch einfache Rechenoperationen wie Multiplikation oder Division kann man dann den gesuchten Wert berechnen.

Um zu überprüfen, ob es sich tatsächlich um eine proportionale oder antiproportionale Zuordnung handelt, kann man die Quotientengleichheit oder Produktgleichheit verwenden. Dabei werden zeilenweise Quotienten oder Produkte gebildet und verglichen.

Es ist auch möglich, Aufgaben zum Dreisatz mit Hilfe von Bruchgleichungen zu lösen. Dabei werden die Einheiten oft weggelassen, um die Gleichung übersichtlicher zu gestalten.

Der Dreisatz ist ein vielseitiges Lösungsverfahren, das bei vielen mathematischen Aufgaben angewendet werden kann. Es ist wichtig, verschiedene Methoden kennenzulernen und den Lösungsweg zu wählen, der am besten geeignet ist.

Der umgekehrte Dreisatz: Lösen von Aufgaben zu antiproportionalen Zuordnungen

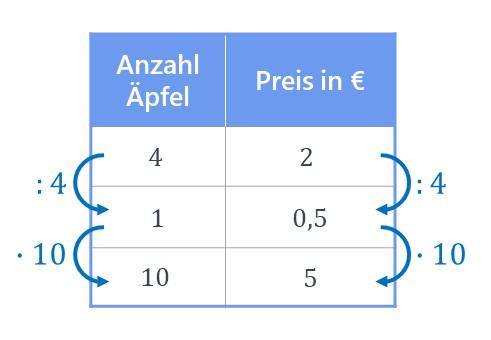
Der umgekehrte Dreisatz ist eine Methode, um Aufgaben zu antiproportionalen Zuordnungen zu lösen. Bei einer antiproportionalen Zuordnung gilt: Je mehr von einer Größe vorhanden ist, desto weniger von der anderen Größe wird benötigt, und umgekehrt.

Um eine solche Aufgabe zu lösen, kann man eine Tabelle verwenden. In der ersten Spalte trägt man die Werte für die eine Größe ein, und in der zweiten Spalte die entsprechenden Werte für die andere Größe.

Man sucht dann einen Zwischenschritt, mit dem man von den gegebenen Werten auf den gesuchten Wert kommen kann. Dabei muss man beachten, dass bei antiproportionalen Zuordnungen auf der gegenüberliegenden Seite immer mit dem Gegenteil gerechnet werden muss.

Eine andere Möglichkeit ist die Verwendung einer Bruchgleichung. Man stellt eine Gleichung auf, in der auf beiden Seiten ein Bruch steht. Man kann dann durch Umstellen und Multiplizieren den gesuchten Wert berechnen.

Es ist auch möglich, die Richtigkeit einer antiproportionalen Zuordnung zu überprüfen. Dazu multipliziert man zeilenweise die Werte und vergleicht die Ergebnisse.

Ein Beispiel für eine Aufgabe zu antiproportionalen Zuordnungen wäre: „10 Bagger benötigen 20 Stunden um eine bestimmte Menge Erde abzutransportieren. Es stehen jetzt aber lediglich 5 Bagger zur Verfügung. Wie viele Stunden brauchen diese 5 Bagger um die gleiche Menge Erde abzutransportieren?“

Überprüfung von proportionalem und antiproportionalem Zusammenhang mit dem Dreisatz

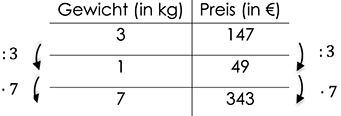
Um zu überprüfen, ob eine Zuordnung proportional oder antiproportional ist, kann der Dreisatz verwendet werden. Bei einer proportionalen Zuordnung gilt: Je mehr von einer Größe vorhanden ist, desto mehr von der anderen Größe gibt es. Bei einer antiproportionalen Zuordnung gilt hingegen: Je mehr von einer Größe vorhanden ist, desto weniger von der anderen Größe gibt es.

Überprüfung einer proportionalen Zuordnung:

• Bilde für jede Zeile den Quotienten aus den beiden Werten.
• Vergleiche die berechneten Quotienten miteinander.
• Wenn alle Quotienten denselben Wert ergeben, handelt es sich um eine proportionale Zuordnung.

Überprüfung einer antiproportionalen Zuordnung:

• Bilde für jede Zeile das Produkt aus den beiden Werten.
• Vergleiche die berechneten Produkte miteinander.
• Wenn alle Produkte denselben Wert ergeben, handelt es sich um eine antiproportionale Zuordnung.

Mit Hilfe des Dreisatzes können also sowohl proportionale als auch antiproportionale Zusammenhänge überprüft werden. Dies ermöglicht eine genaue Analyse und Lösung mathematischer Aufgaben.

Der Dreisatz ist eine mathematische Methode, um Proportionen und Verhältnisse zu berechnen. Er besteht aus drei Schritten und ermöglicht es, fehlende Werte zu ermitteln. Mit dem Dreisatz lässt sich das Verständnis für mathematische Zusammenhänge verbessern und er findet Anwendung in verschiedenen Bereichen des Alltags.