Eine Asymptote ist eine mathematische Linie, die sich einer Kurve immer weiter annähert, aber sie niemals berührt oder schneidet. Sie spielt eine wichtige Rolle bei der Untersuchung von Funktionen und kann helfen, deren Verhalten im Unendlichen zu verstehen. In diesem Artikel werden wir uns genauer mit dem Konzept der Asymptoten befassen und ihre Bedeutung in der Mathematik erklären.
- Mülltonnen Versteck: Praktische Anleitung für den eigenen Unterstand
- Grüne Wandgestaltung: DIY Ideen für eine Pflanzenwand
- Die Kristallnacht – Die staatlich organisierten Gewaltaktionen gegen Juden am 9. November 1938
- Wann Rosen zurückschneiden: Tipps für den richtigen Schnitt
- Eddie Murphy: Wie alt ist der Schauspieler?
Was ist eine Asymptote? Eine Erklärung und Beispiele
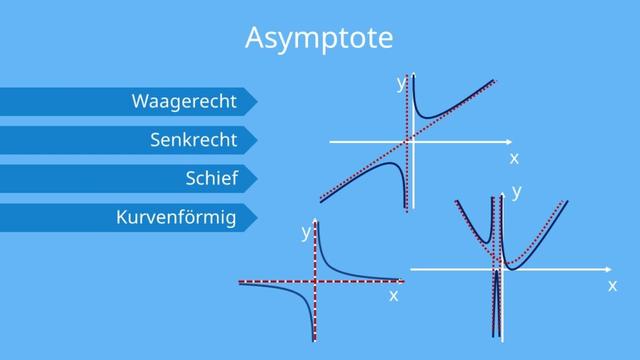
Eine Asymptote ist eine Kurve oder Linie, an die sich der Graph einer Funktion immer weiter annähert. Der Abstand zwischen dem Graphen und der Asymptote wird beliebig klein, wenn man sich in x-Richtung immer weiter vom Ursprung entfernt und den Funktionsgraphen betrachtet.
Es gibt verschiedene Typen von Asymptoten:
1. Waagrechte Asymptoten: Sie sind waagrechte Geraden, die parallel zur x-Achse verlaufen. Ihre Funktionsgleichung hat die Form y = c, wobei c eine konstante Zahl ist.
2. Senkrechte Asymptoten: Sie sind senkrechte Geraden, die parallel zur y-Achse verlaufen. Da sie nicht durch eine Funktionsgleichung beschrieben werden können, werden sie durch die Gleichung x = a beschrieben, wobei a eine Polstelle ist.
3. Schiefe Asymptoten: Sie sind Geraden, die weder waagrecht noch senkrecht verlaufen. Ihre Funktionsgleichung hat die Form y = mx + b, wobei m die Steigung der Asymptote und b der Schnittpunkt mit der y-Achse ist. Manchmal werden sie auch als schräge Asymptoten bezeichnet.
4. Kurvenförmige Asymptoten: Das asymptotische Verhalten des Funktionsgraphen ist kurvenförmig, wenn der Zählergrad der Funktion um mehr als eins größer ist als der Nennergrad.
Um die Art einer Asymptote zu bestimmen, vergleicht man den Zählergrad mit dem Nennergrad einer gebrochenrationalen Funktion. Anhand dieser Vergleichsregel kann man den Typ der Asymptote bestimmen.
Für die e-Funktion gibt es eine waagrechte Asymptote bei y = 0, unabhängig von Streckungen oder Verschiebungen in x- oder y-Richtung.
Die Berechnung von Asymptoten beinhaltet oft auch die Bestimmung von Grenzwerten, z.B. im Unendlichen. Es gibt verschiedene Möglichkeiten, Grenzwerte für verschiedene Funktionentypen zu berechnen.
Das sind die grundlegenden Informationen über Asymptoten und ihre Berechnung.
Arten von Asymptoten: Waagrechte, senkrechte und schräge Asymptoten
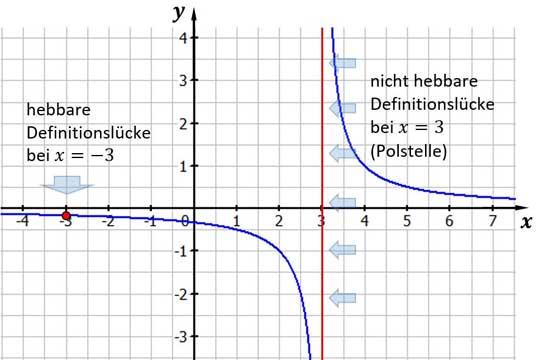
Eine Asymptote ist eine Kurve oder Linie, an die sich der Graph einer Funktion immer weiter annähert. Der Abstand zwischen dem Graphen und der Asymptote wird beliebig klein, wenn man sich in x-Richtung immer weiter vom Ursprung entfernt und dabei den Funktionsgraphen betrachtet. Dieses Verhalten im Unendlichen wird auch als Verhalten im Unendlichen bezeichnet.
Es gibt vier verschiedene Typen von Asymptoten:
1. Waagrechte Asymptoten: Sie verlaufen parallel zur x-Achse und ihre Funktionsgleichung hat die Form y = c, wobei c eine konstante Zahl ist.
2. Senkrechte Asymptoten: Sie verlaufen parallel zur y-Achse und können nicht mithilfe einer Funktionsgleichung beschrieben werden. Stattdessen werden sie durch die Gleichung x = a beschrieben, wobei a eine Polstelle genannt wird.
3. Schiefe Asymptoten: Sie sind Geraden, die weder waagrecht noch senkrecht verlaufen. Ihre Funktionsgleichung hat die Form y = mx + b, wobei m die Steigung der Asymptote und b der Schnittpunkt mit der y-Achse ist.
4. Kurvenförmige Asymptoten: Diese treten auf, wenn der Zählergrad des Bruchs um mehr als eins größer ist als der Nennergrad. Das asymptotische Verhalten des Funktionsgraphen ist dann kurvenförmig.
Um die Art einer Asymptote zu bestimmen, vergleicht man den Zählergrad mit dem Nennergrad des Bruchs. Je nachdem, ob der Zählergrad kleiner, gleich oder größer ist als der Nennergrad, kann man auf eine waagrechte, senkrechte, schiefe oder kurvenförmige Asymptote schließen.
Bei gebrochenrationalen Funktionen gibt es ein konkretes Vorgehen zur Bestimmung der Asymptoten. Man vergleicht den Zählergrad mit dem Nennergrad und betrachtet die Nullstellen des Nenners. Je nachdem, ob der Bruch vollständig gekürzt ist und der Nenner noch eine Nullstelle besitzt, kann man auf eine senkrechte Asymptote schließen.
Für die e-Funktion gilt, dass sie eine waagrechte Asymptote bei y = 0 hat. Selbst bei Streckungen oder Verschiebungen ändert sich das asymptotische Verhalten nicht.
Um Asymptoten zu berechnen, muss man verschiedene Arten unterscheiden und Grenzwerte bestimmen. Das Berechnen von Asymptoten beinhaltet also auch das Berechnen von Grenzwerten.
Zusammenfassend gibt es waagrechte, senkrechte, schiefe und kurvenförmige Asymptoten. Die Art einer Asymptote hängt vom Vergleich des Zählergrades mit dem Nennergrad ab. Bei gebrochenrationalen Funktionen gibt es ein konkretes Vorgehen zur Bestimmung der Asymptoten. Auch die e-Funktion hat eine spezielle waagrechte Asymptote bei y = 0. Das Berechnen von Asymptoten beinhaltet das Bestimmen von Grenzwerten.
Wie berechnet man Asymptoten? Schritt-für-Schritt Anleitung mit Beispielen
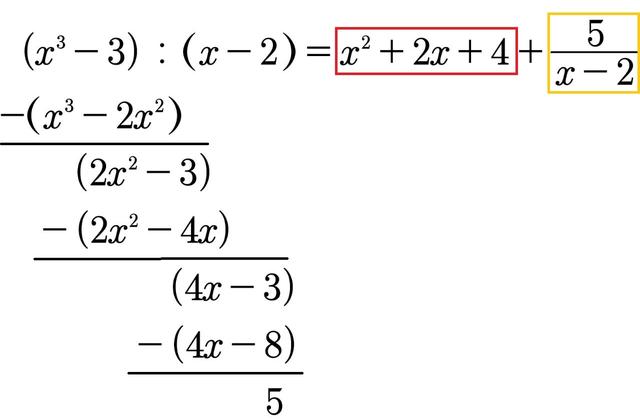
Wie berechnet man Asymptoten? Schritt-für-Schritt Anleitung mit Beispielen
Eine Asymptote ist eine Kurve oder Linie, an die sich der Graph einer Funktion immer weiter annähert. Um Asymptoten zu berechnen, muss man verschiedene Arten unterscheiden:
1. Waagrechte Asymptote:
– Überprüfe den Zählergrad und den Nennergrad der Funktion.
– Wenn der Zählergrad kleiner ist als der Nennergrad, gibt es eine waagrechte Asymptote bei y = 0.
– Die Funktionsgleichung dieser waagrechten Asymptote lautet y = 0.
2. Schiefe Asymptote:
– Überprüfe den Zählergrad und den Nennergrad der Funktion.
– Wenn der Zählergrad um 1 größer ist als der Nennergrad, gibt es eine schiefe Asymptote.
– Um die Funktionsgleichung dieser schiefen Asymptote zu bestimmen, führt man eine Polynomdivision durch und betrachtet den Grenzwert für x gegen Unendlich.
3. Kurvenförmige Asymptote:
– Überprüfe den Zählergrad und den Nennergrad der Funktion.
– Wenn der Zählergrad mehr als 1 größer ist als der Nennergrad, hat der Funktionsgraph ein kurvenförmiges asymptotisches Verhalten.
– Um die Funktionsgleichung dieser kurvenförmigen Asymptote zu bestimmen, führt man ebenfalls eine Polynomdivision durch und betrachtet den Grenzwert für x gegen Unendlich.
Beispiel:
Gegeben ist die Funktion f(x) = (2x^2 + 3x – 1) / (x + 1).
1. Überprüfe den Zählergrad und den Nennergrad:
– Der Zählergrad beträgt 2 und der Nennergrad beträgt 1.
2. Da der Zählergrad um 1 größer ist als der Nennergrad, gibt es eine schiefe Asymptote.
– Führe eine Polynomdivision durch: (2x^2 + 3x – 1) / (x + 1).
– Das Ergebnis der Polynomdivision ist f(x) = 2x – 1.
– Betrachte den Grenzwert für x gegen Unendlich: lim(x->∞) f(x) = lim(x->∞) (2x – 1).
– Der Grenzwert ergibt sich zu ∞, also hat die Funktion eine schiefe Asymptote mit der Funktionsgleichung y = 2x – 1.
Damit sind die Schritte zur Berechnung von Asymptoten abgeschlossen. Es ist wichtig zu beachten, dass diese Methode nur für gebrochenrationale Funktionen gilt. Andere Funktionstypen können unterschiedliche asymptotische Verhaltensweisen aufweisen.
Asymptoten bei gebrochenrationalen Funktionen: Bestimmung und Typen
Eine Asymptote ist eine Kurve oder Linie, an die sich der Graph einer Funktion immer weiter annähert. Der Abstand zwischen dem Graphen und der Asymptote wird dabei beliebig klein, wenn man sich in x-Richtung immer weiter vom Ursprung entfernt.
Es gibt vier verschiedene Typen von Asymptoten: waagrechte, senkrechte, schiefe und kurvenförmige Asymptoten.
– Waagrechte Asymptoten sind waagrechte Geraden, die parallel zur x-Achse verlaufen. Ihre Funktionsgleichung hat die Form y = c, wobei c eine konstante Zahl ist.
– Senkrechte Asymptoten sind senkrechte Geraden, die parallel zur y-Achse verlaufen. Sie können nicht durch eine Funktionsgleichung beschrieben werden.
– Schiefe Asymptoten sind Geraden, die weder waagrecht noch senkrecht verlaufen. Ihre Funktionsgleichung hat die Form y = mx + b, wobei m die Steigung der Asymptote und b der Schnittpunkt mit der y-Achse ist.
– Kurvenförmige Asymptoten sind keine Geraden, sondern Kurven. Ihre Funktionsgleichung kann nicht allgemein angegeben werden.
Für gebrochenrationale Funktionen gibt es ein konkretes Vorgehen zur Bestimmung der Asymptoten. Man vergleicht den Zählergrad mit dem Nennergrad:
– Wenn der Zählergrad kleiner ist als der Nennergrad, gibt es eine waagrechte Asymptote bei y = 0.
– Wenn der Zählergrad gleich dem Nennergrad ist, gibt es eine waagrechte Asymptote bei y = a/b, wobei a der Koeffizient des höchsten Potenzterms im Zählerpolynom ist und b der Koeffizient des höchsten Potenzterms im Nennerpolynom.
– Wenn der Zählergrad um 1 größer ist als der Nennergrad, gibt es eine schiefe Asymptote. Die Funktionsgleichung dieser Asymptote kann durch Polynomdivision und Grenzwertbetrachtung bestimmt werden.
– Wenn der Zählergrad mehr als 1 größer ist als der Nennergrad, hat der Funktionsgraph ein kurvenförmiges asymptotisches Verhalten. Auch hier wird die Funktionsgleichung der Asymptoten durch Polynomdivision und Grenzwertbetrachtung ermittelt.
Auch die e-Funktion besitzt eine waagrechte Asymptote bei y = 0. Eine Verschiebung in x-Richtung oder Stauchung in x- oder y-Richtung ändert nichts an dieser Asymptote.
Um Asymptoten zu berechnen, muss man verschiedene Arten unterscheiden. Für waagrechte Asymptoten vergleicht man den Zählergrad mit dem Nennergrad. Für schiefe und kurvenförmige Asymptoten verwendet man Polynomdivision und Grenzwertbetrachtung.
Es gibt also verschiedene Methoden zur Bestimmung von Asymptoten bei gebrochenrationalen Funktionen.
Asymptotisches Verhalten der e-Funktion: Waagrechte Asymptote und Verschiebungen
Eine wichtige Funktion, deren asymptotisches Verhalten man kennen sollte, ist die e-Funktion. Die normale Exponentialfunktion besitzt eine waagrechte Asymptote bei y=0. Der Graph der Funktion nähert sich dieser Asymptote für immer kleiner werdende x-Werte immer näher an. Auch wenn die normale e-Funktion in x- oder in y-Richtung gestaucht wird, bleibt die Asymptote die selbe. Selbst bei einer Verschiebung in x-Richtung ändert sich daran nichts. Das bedeutet, dass die Funktion das selbe asymptotische Verhalten wie die Funktion f(x)=e^x zeigt. Eine Verschiebung in y-Richtung verschiebt allerdings auch die waagrechte Asymptote der Funktion. So lautet zum Beispiel für die Funktion g(x)=e^x+2 ihre waagrechte Asymptote y=2.
Zusammenfassend kann man sagen, dass eine Asymptote eine Kurve oder Linie ist, an die sich der Graph einer Funktion immer weiter annähert. Im Unendlichen wird der Abstand zwischen dem Graphen und der Asymptote sehr klein. Um Asymptoten zu berechnen, muss man verschiedene Arten unterscheiden:
– Wenn der Zählergrad einer gebrochenrationalen Funktion kleiner ist als der Nennergrad, gibt es eine waagrechte Asymptote bei y=0.
– Wenn der Zählergrad gleich dem Nennergrad ist, gibt es ebenfalls eine waagrechte Asymptote bei y=0.
– Wenn der Zählergrad um 1 größer ist als der Nennergrad, gibt es eine schiefe Asymptote.
– Wenn der Zählergrad mehr als 1 größer ist als der Nennergrad, gibt es eine kurvenförmige Asymptote.
Wenn du eine Asymptote berechnest, bestimmst du immer auch einen Grenzwert, zum Beispiel im Unendlichen. Möchtest du mehr über die Grenzwerte verschiedener Funktionentypen wissen, dann schau dir unser Video dazu an!
Grenzwerte und Asymptoten: Zusammenhang und weitere Informationen
Grenzwerte und Asymptoten sind eng miteinander verbunden. Grenzwerte geben an, wie sich eine Funktion für immer größere oder kleinere Werte von x verhält. Asymptoten sind Kurven oder Linien, denen sich der Graph einer Funktion immer weiter annähert.
Eine waagrechte Asymptote tritt auf, wenn der Zählergrad der Funktion kleiner ist als der Nennergrad. Die Funktionsgleichung dieser Asymptote lautet y = 0. Das bedeutet, dass der Graph der Funktion für immer größer werdende oder kleiner werdende x-Werte die waagrechte Gerade y = 0 erreicht.
Eine schräge Asymptote tritt auf, wenn der Zählergrad um eins größer ist als der Nennergrad. Um die Funktionsgleichung dieser Asymptote zu bestimmen, führt man eine Polynomdivision durch und betrachtet den Grenzwert für x gegen Unendlich. Dieser Grenzwert gibt die Steigung der schiefen Asymptote an.
Wenn der Zählergrad mehr als eins größer ist als der Nennergrad, hat die Funktion ein kurvenförmiges asymptotisches Verhalten. Auch hier wird die Funktionsgleichung durch Polynomdivision und Grenzwertbetrachtung ermittelt.
Es ist wichtig zu beachten, dass nicht alle Funktionen Asymptoten haben. Manche Funktionen können auch mehrere Asymptoten haben.
Um die verschiedenen Arten von Asymptoten zu berechnen, vergleicht man den Zähler- und den Nennergrad der gebrochenrationalen Funktion. Je nachdem ob sie gleich sind oder in welchem Verhältnis sie zueinander stehen, kann man den Typ der Asymptote bestimmen.
Die Kenntnis von Grenzwerten und Asymptoten ist wichtig für die Kurvendiskussion einer Funktion. Sie ermöglichen es, das Verhalten des Funktionsgraphen im Unendlichen zu beschreiben und wichtige Eigenschaften der Funktion zu analysieren.
In der Mathematik ist eine Asymptote eine gerade Linie, die sich immer weiter einer Kurve annähert, aber sie nie berührt oder schneidet. Asymptoten sind wichtig, um das Verhalten von Funktionen zu analysieren und Grenzwerte zu bestimmen. Sie ermöglichen es uns, unendlich große oder kleine Werte einer Funktion zu verstehen. Durch das Verständnis von Asymptoten können wir komplexe mathematische Probleme besser lösen und Zusammenhänge zwischen Funktionen erkennen.

