Die Standardabweichung ist ein wichtiger statistischer Wert, der uns Aufschluss über die Streuung von Daten gibt. Sie zeigt uns, wie weit die einzelnen Werte im Durchschnitt von ihrem Mittelwert abweichen. In diesem Artikel erfahren Sie mehr darüber, was die Standardabweichung genau aussagt und wie sie interpretiert werden kann.
- Aufnäher individuell gestalten: Bestellen Sie bei uns im Shop oder stellen Sie eine kostenlose Anfrage
- Leckere Trinkschokolade am Stiel selbstgemacht – Geschenkidee!
- Erstelle dein eigenes Audio-Gästebuch und genieße Erlebnisse – jetzt anmelden!
- Ursachen, Symptome und Behandlung von Zwangsstörungen
- Tonkabohne: Verwendung, Vorteile und optimierte Inhalte auf unserer Webseite
Die Standardabweichung: Ein Maß für die Streubreite von Werten
Die Standardabweichung ist ein statistisches Maß, das verwendet wird, um die Streubreite der Werte eines Merkmals um den Mittelwert zu quantifizieren. Vereinfacht ausgedrückt gibt die Standardabweichung an, wie weit die gemessenen Ausprägungen eines Merkmals im Durchschnitt vom Mittelwert entfernt sind. Sie wird häufig in Umfragen und Studien verwendet, um die Varianz der Daten zu analysieren.
Die Berechnung der Standardabweichung erfolgt durch die Quadratwurzel der Varianz. Die Varianz ist definiert als die durchschnittliche quadratische Abweichung der einzelnen Werte vom Mittelwert. Die Standardabweichung wird oft mit dem Symbol „σ“ für eine Zufallsvariable oder „s“ für eine Stichprobe angegeben.
Ein wichtiger Aspekt der Standardabweichung ist, dass sie immer die gleiche Maßeinheit wie das untersuchte Merkmal besitzt. Dadurch ist es einfacher, sie zu interpretieren als die Varianz, da sie direkt auf den Wertebereich des Merkmals bezogen ist.
Eine kleinere Standardabweichung deutet in der Regel darauf hin, dass die gemessenen Ausprägungen des Merkmals enger um den Mittelwert liegen. Eine größere Standardabweichung hingegen zeigt eine stärkere Streuung der Daten an.
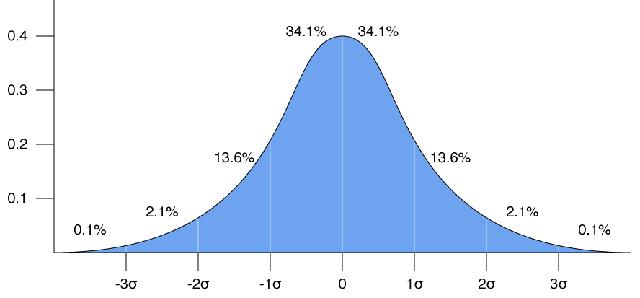
Für normalverteilte Merkmale gilt eine Faustregel: Innerhalb einer Entfernung von einer Standardabweichung vom Mittelwert liegen rund 68 Prozent aller Antwortwerte. Innerhalb von zwei Standardabweichungen sind es rund 95 Prozent aller Werte. Abweichungen, die größer als zwei Standardabweichungen sind, werden als Ausreißer bezeichnet.
Als Beispiel kann man sich vorstellen, dass 1.000 Personen nach ihren monatlichen Handyrechnungen befragt wurden. Der Mittelwert liegt bei 40 Euro und die Standardabweichung beträgt 27 Euro. Das bedeutet, dass die durchschnittliche Entfernung aller Antworten zum Mittelwert 27 Euro beträgt.
In einem weiteren Beispiel wurden 1.000 Personen gefragt, wie viel Geld sie im Schnitt ausgeben, wenn sie mittags essen gehen. Der Mittelwert liegt bei 4,50 Euro und die Standardabweichung bei s = 0,60 Euro. Dies bedeutet, dass die durchschnittliche Entfernung aller Antworten zum Mittelwert 0,60 Euro beträgt. Aufgrund der beschriebenen Faustformel lässt sich ableiten, dass rund 68 Prozent aller Befragten zwischen 3,90 Euro und 5,10 Euro ausgeben (4,50 +/- 0,60 Euro). Rund 95 Prozent geben zwischen 3,30 Euro und 5,70 Euro aus (4,50 +/- 2 mal 0,60 Euro).
Bitte beachten Sie jedoch, dass die Definitionen in diesem Statistik-Lexikon vereinfachte Erläuterungen sind und möglicherweise nicht vollständig den wissenschaftlichen Standards entsprechen.
Die Bedeutung der Standardabweichung in der Statistik
Die Standardabweichung ist ein wichtiges Maß in der Statistik, um die Streubreite der Werte eines Merkmals um den Mittelwert zu beschreiben. Sie gibt an, wie stark die gemessenen Ausprägungen eines Merkmals vom Durchschnitt abweichen. Eine größere Standardabweichung deutet auf eine stärkere Streuung hin, während eine kleinere Standardabweichung darauf hindeutet, dass die Werte enger um den Mittelwert liegen.
Die Berechnung der Standardabweichung erfolgt über die Quadratwurzel der Varianz. Die Standardabweichung wird oft mit dem Symbol „σ“ für eine Zufallsvariable oder „s“ für eine Stichprobe angegeben. Sie hat immer die gleiche Maßeinheit wie das untersuchte Merkmal, was ihre Interpretation im Vergleich zur Varianz erleichtert.
Für normalverteilte Merkmale gilt eine Faustformel: Innerhalb einer Standardabweichung nach oben und unten vom Mittelwert liegen rund 68 Prozent aller Antwortwerte. Innerhalb von zwei Standardabweichungen sind es rund 95 Prozent aller Werte. Abweichungen jenseits dieser Grenzen werden als Ausreißer bezeichnet.
In unserem Beispiel wurde gefragt, wie hoch die monatliche Handyrechnung von 1.000 Personen ist. Der Mittelwert lag bei 40 Euro und die Standardabweichung bei 27 Euro. Das bedeutet, dass die durchschnittliche Entfernung aller Antworten zum Mittelwert 27 Euro beträgt.
Es ist wichtig zu beachten, dass diese Definitionen vereinfacht sind und möglicherweise nicht allen wissenschaftlichen Standards entsprechen.
Interpretation und Aussagekraft der Standardabweichung
Die Standardabweichung ist ein wichtiges Maß, um die Streubreite der Werte eines Merkmals um den Mittelwert zu bestimmen. Sie gibt an, wie weit die gemessenen Ausprägungen eines Merkmals im Durchschnitt vom Mittelwert entfernt sind. Eine kleinere Standardabweichung deutet darauf hin, dass die gemessenen Werte enger um den Mittelwert liegen, während eine größere Standardabweichung auf eine stärkere Streuung hindeutet.
Die Interpretation der Standardabweichung wird durch ihre Maßeinheit erleichtert, da sie immer die gleiche Einheit wie das untersuchte Merkmal besitzt. Im Vergleich zur Varianz ist die Interpretation der Standardabweichung einfacher.
Für normalverteilte Merkmale gilt eine Faustformel: Innerhalb einer Standardabweichung nach oben und unten vom Mittelwert liegen rund 68 Prozent aller Antwortwerte. Innerhalb von zwei Standardabweichungen sind es rund 95 Prozent aller Werte. Abweichungen jenseits dieser Grenzen werden als Ausreißer bezeichnet.
Ein Beispiel zur Veranschaulichung: Wenn 1.000 Personen gefragt werden, wie hoch ihre monatliche Handyrechnung ist und der Mittelwert bei 40 Euro liegt mit einer Standardabweichung von 27 Euro, bedeutet dies, dass die durchschnittliche Entfernung aller Antworten zum Mittelwert 27 Euro beträgt.
Es ist jedoch wichtig zu beachten, dass diese Definitionen vereinfacht sind und möglicherweise nicht vollständig den wissenschaftlichen Standards entsprechen.
Wie die Standardabweichung die Verteilung von Daten beschreibt
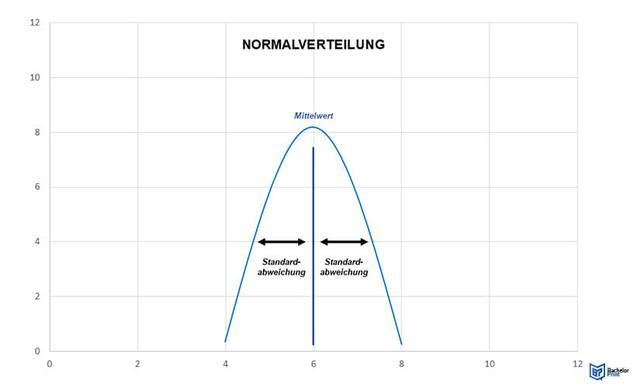
Die Standardabweichung ist ein Maß für die Streubreite der Werte eines Merkmals rund um dessen Mittelwert. Sie gibt an, wie weit die gemessenen Ausprägungen eines Merkmals im Durchschnitt vom Durchschnittswert entfernt sind. Eine kleinere Standardabweichung bedeutet, dass die Werte enger um den Mittelwert liegen, während eine größere Standardabweichung auf eine stärkere Streuung hinweist.
Um die Standardabweichung zu berechnen, wird die Quadratwurzel der Varianz verwendet. Das Symbol für die Standardabweichung einer Zufallsvariable ist σ, während für eine Stichprobe das Symbol s verwendet wird. Die Standardabweichung hat immer dieselbe Maßeinheit wie das untersuchte Merkmal, was ihre Interpretation im Vergleich zur Varianz erleichtert.
Für normalverteilte Merkmale gilt eine Faustformel: Innerhalb einer Standardabweichung vom Mittelwert liegen etwa 68 Prozent aller Antwortwerte. Innerhalb von zwei Standardabweichungen sind es rund 95 Prozent aller Werte. Abweichungen jenseits dieser Grenzen werden als Ausreißer bezeichnet.
Ein Beispiel: Wenn 1.000 Personen gefragt wurden, wie hoch ihre monatliche Handyrechnung ist und der Mittelwert bei 40 Euro liegt mit einer Standardabweichung von 27 Euro, bedeutet dies, dass die durchschnittliche Entfernung aller Antworten zum Mittelwert 27 Euro beträgt.
Es ist wichtig zu beachten, dass diese Definitionen vereinfacht sind und möglicherweise nicht allen wissenschaftlichen Standards entsprechen.
Der Zusammenhang zwischen Mittelwert und Standardabweichung
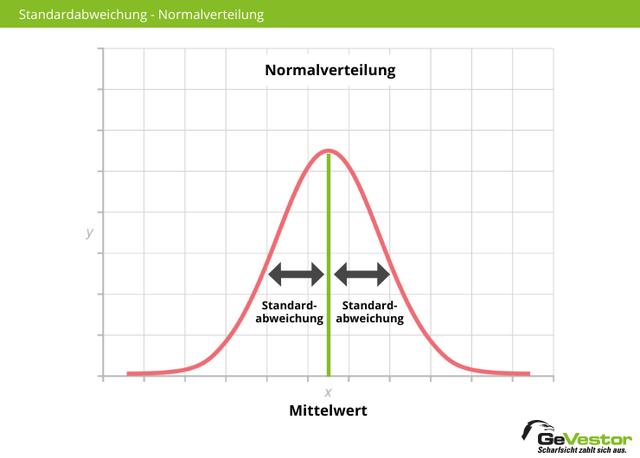
Die Standardabweichung ist eng mit dem Mittelwert eines Merkmals verbunden. Sie gibt an, wie stark die gemessenen Ausprägungen eines Merkmals um den Durchschnitt herum streuen. Eine kleine Standardabweichung deutet darauf hin, dass die Werte des Merkmals eher nah beieinander liegen, während eine große Standardabweichung auf eine größere Streuung hinweist.
Wenn der Mittelwert einer Stichprobe erhöht wird, hat dies in der Regel auch Auswirkungen auf die Standardabweichung. Wenn die Werte um den höheren Mittelwert herum gestreut sind, wird die durchschnittliche Entfernung zum Mittelwert größer und somit auch die Standardabweichung.
Umgekehrt gilt: Wenn der Mittelwert einer Stichprobe verringert wird, werden die Werte tendenziell enger um den niedrigeren Mittelwert gestreut. Dadurch nimmt auch die durchschnittliche Entfernung zum Mittelwert ab und somit auch die Standardabweichung.
Es besteht also ein direkter Zusammenhang zwischen dem Mittelwert und der Standardabweichung eines Merkmals. Eine Änderung des Mittelwerts führt zu einer entsprechenden Änderung der Streuung der Werte um diesen Durchschnittswert herum.
Zusammenfassend lässt sich sagen, dass der Mittelwert und die Standardabweichung wichtige Kennzahlen sind, um das Verhalten von Daten zu beschreiben und zu analysieren. Der Mittelwert gibt einen zentralen Wert an, während die Standardabweichung Informationen über die Streuung der Daten liefert.
Die Faustformel der Standardabweichung und ihre Anwendung
Anwendung der Faustformel
Die Faustformel der Standardabweichung besagt, dass innerhalb einer Entfernung von einer Standardabweichung nach oben und unten vom Mittelwert rund 68 Prozent aller Antwortwerte liegen. Das bedeutet, dass die meisten gemessenen Ausprägungen eines Merkmals in einem relativ engen Bereich um den Mittelwert herum liegen.
Wenn man den Umkreis auf zwei Standardabweichungen erweitert, sind bereits rund 95 Prozent aller Werte enthalten. Das heißt, dass die Streubreite der gemessenen Ausprägungen größer wird und es auch mehr Ausreißer gibt.
Diese Faustformel ist besonders nützlich bei normalverteilten Merkmalen, da sie eine schnelle Einschätzung darüber ermöglicht, wie weit die gemessenen Werte um den Mittelwert streuen.
Beispielanwendung
Nehmen wir an, wir haben eine Stichprobe von 1.000 Personen befragt, wie viel Geld sie im Schnitt ausgeben, wenn sie mittags essen gehen. Der Mittelwert liegt bei 4,50 Euro und die Standardabweichung beträgt s = 0,60 Euro.
Anhand der Faustformel können wir ableiten, dass rund 68 Prozent aller Befragten zwischen 3,90 Euro und 5,10 Euro ausgeben (4,50 +/- 0,60 Euro). Rund 95 Prozent geben zwischen 3,30 Euro und 5,70 Euro aus (4,50 +/- 2 mal 0,60 Euro).
Durch die Anwendung der Faustformel erhalten wir einen guten Überblick über die Streubreite der gemessenen Ausprägungen und können schnell beurteilen, wie repräsentativ unsere Stichprobe ist.
Insgesamt lässt sich sagen, dass die Standardabweichung eine wichtige statistische Kennzahl ist, die Auskunft darüber gibt, wie stark die einzelnen Werte einer Verteilung um den Durchschnitt streuen. Sie ermöglicht es uns, die Varianz innerhalb einer Datenmenge zu bestimmen und somit Rückschlüsse auf deren Streuung und Homogenität zu ziehen. Die Standardabweichung ist daher ein nützliches Werkzeug in der Datenanalyse und kann dabei helfen, Muster und Trends zu erkennen sowie Vergleiche zwischen verschiedenen Gruppen oder Zeitperioden anzustellen.