Was ist Flächeninhalt und wie berechnet man ihn?

Der Begriff „Flächeninhalt“ bezieht sich auf die Größe einer Fläche. Er gibt an, wie viel Raum eine bestimmte Fläche einnimmt und wird in Quadratmetern gemessen. Der Flächeninhalt ist ein wichtiges Konzept in der Geometrie und spielt eine entscheidende Rolle bei Berechnungen von Grundstücken, Räumen oder geometrischen Figuren. Dieser Artikel erklärt, was der Flächeninhalt ist und wie er berechnet werden kann.

Was ist Flächeninhalt und wie wird er berechnet?

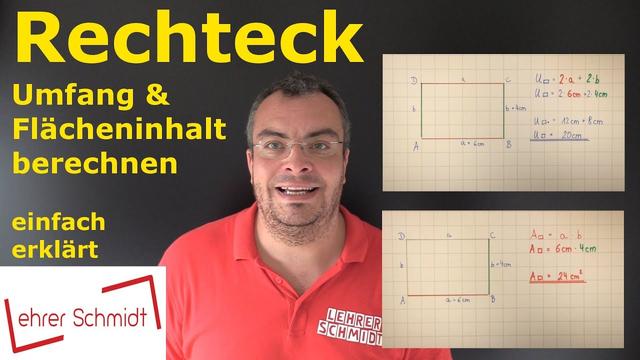
Definition des Flächeninhalts

Der Flächeninhalt ist ein Maß für die Größe eines zweidimensionalen Objekts oder einer Figur. Er gibt an, wie groß die Fläche dieser Figur ist. Der Flächeninhalt wird oft auch einfach als „Fläche“ bezeichnet, was jedoch missverständlich sein kann, da dieser Begriff sowohl das Objekt selbst als auch seine Größe umfassen kann. Zum Beispiel kann man sagen „diese Fläche malen wir grün an“ oder „die Fläche des Ackers beträgt einen halben Hektar“.

Im dreidimensionalen Raum spricht man meist von der „Oberfläche“ eines Körpers, wenn man über Flächen spricht. Genauer gesagt bezieht sich dies auf den „Oberflächeninhalt“ eines Körpers.

Berechnung des Flächeninhalts

Die Basiseinheit des Flächeninhalts ist der Quadratmeter (m²). Man kann jedoch jede andere Längeneinheit quadrieren, um eine Flächeneinheit zu erhalten. Zum Beispiel sind 100 Meter mal 100 Meter ein Hektar und (1 cm)² sind ein Quadratzentimeter.

Für viele Figuren gibt es einfache Formeln zur Berechnung des Flächeninhalts. Zum Beispiel ist die Fläche eines Rechtecks das Produkt von zwei benachbarten Seitenlängen.

Wenn eine Figur von einer beliebig geformten Kurve begrenzt wird, die der Graph einer Funktion ist, kann man ihren Flächeninhalt mithilfe der Integralrechnung berechnen.

Der Flächeninhalt einer zusammengesetzten Figur ist die Summe der Einzelflächen. Die Analytische Geometrie bietet weitere Möglichkeiten zur Bestimmung von Flächeninhalten. Zum Beispiel ist die Fläche eines Parallelogramms der Betrag des Kreuzprodukts (Vektorprodukts) der beiden Vektoren, die es aufspannen.

Insgesamt gibt es verschiedene Methoden und Formeln, um den Flächeninhalt einer Figur zu berechnen, je nach ihrer Form und den gegebenen Informationen.

Die Bedeutung und Berechnung des Flächeninhalts

Die Bedeutung des Flächeninhalts

Der Flächeninhalt ist ein Maß für die Größe eines zweidimensionalen Objekts oder einer Figur. Er gibt an, wie viel Fläche von dem Objekt eingenommen wird. Der Flächeninhalt kann verwendet werden, um die Größe von verschiedenen geometrischen Formen zu vergleichen, wie zum Beispiel Quadraten, Rechtecken oder Kreisen. Auch bei realen Objekten wie einem Fußballfeld oder der Bundesrepublik Deutschland kann der Flächeninhalt angegeben werden, um ihre Größe zu beschreiben.

Es ist wichtig zu beachten, dass der Begriff „Fläche“ sowohl das Objekt selbst als auch seine Größe bezeichnen kann. Deshalb wird oft der Begriff „Flächeninhalt“ verwendet, um deutlich zu machen, dass es sich um die Größe der Fläche handelt.

Die Berechnung des Flächeninhalts

Für viele geometrische Figuren gibt es einfache Formeln zur Berechnung des Flächeninhalts. Zum Beispiel ist die Fläche eines Rechtecks das Produkt seiner beiden benachbarten Seitenlängen: A = Länge * Breite.

Wenn eine Figur von einer beliebig geformten Kurve begrenzt wird, die der Graph einer Funktion ist, kann man ihren Flächeninhalt mithilfe der Integralrechnung berechnen. Das Integral über den Bereich zwischen der Funktion und der x-Achse liefert den Flächeninhalt.

Bei zusammengesetzten Figuren ist der Flächeninhalt die Summe der Einzelflächen. Man kann die Fläche einer zusammengesetzten Figur berechnen, indem man die Flächen der einzelnen Teile addiert.

In der analytischen Geometrie gibt es auch andere Methoden zur Bestimmung von Flächeninhalten. Zum Beispiel kann die Fläche eines Parallelogramms als Betrag des Kreuzprodukts der beiden Vektoren berechnet werden, die es aufspannen.

Es ist wichtig, den Flächeninhalt korrekt zu berechnen, um genaue Messungen und Vergleiche durchführen zu können. Der Quadratmeter (m²) ist die Basiseinheit für den Flächeninhalt. Es ist jedoch auch möglich, jede andere Längeneinheit zu quadrieren, um eine Flächeneinheit zu erhalten.

Zusammenfassend kann gesagt werden, dass der Flächeninhalt ein wichtiges Konzept in der Geometrie ist, um die Größe von zweidimensionalen Objekten und Figuren zu beschreiben und zu vergleichen. Es gibt verschiedene Methoden zur Berechnung des Flächeninhalts, je nach Form der Figur oder des Objekts.

Flächeninhalt: Definition und Berechnungsmethoden

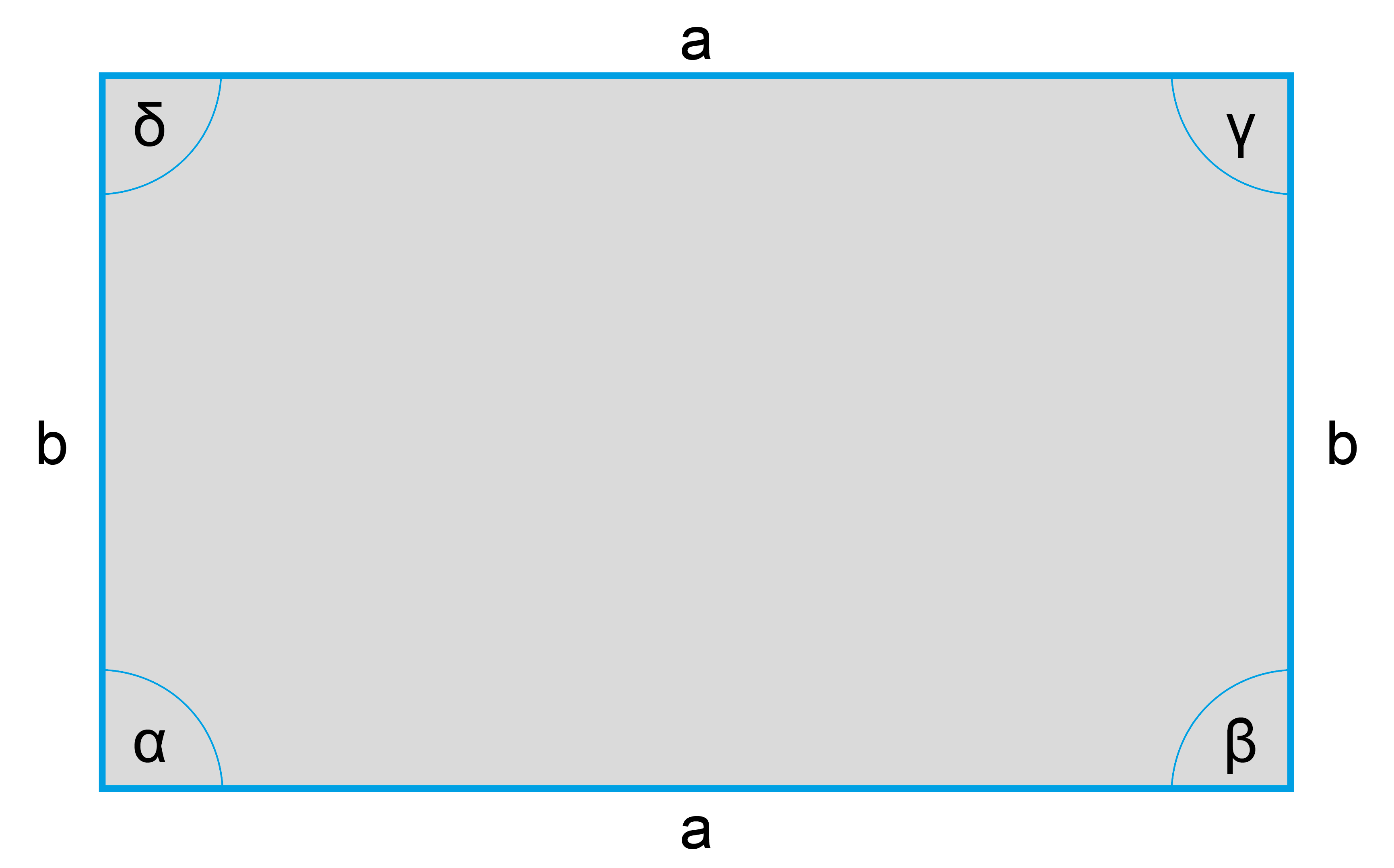
Definition des Flächeninhalts

Der Flächeninhalt ist ein Maß für die Größe eines zweidimensionalen Objekts oder einer Figur. Er gibt an, wie viel Fläche eine Figur in der Ebene einnimmt. Oft wird auch einfach nur von „Fläche“ gesprochen, was jedoch zu Missverständnissen führen kann, da damit sowohl das Objekt selbst als auch seine Größe gemeint sein kann. Um diese Unterscheidung zu verdeutlichen, spricht man bei Flächen im dreidimensionalen Raum meist von der „Oberfläche“.

Die Basiseinheit des Flächeninhalts ist der Quadratmeter (m²). Man kann jedoch jede andere Längeneinheit quadrieren, um eine Flächeneinheit zu erhalten. Zum Beispiel entspricht 100 Meter mal 100 Meter einem Hektar und (1 cm)² einem Quadratzentimeter.

Berechnung des Flächeninhalts

Für viele Figuren gibt es einfache Formeln zur Berechnung des Flächeninhalts. So ist zum Beispiel die Fläche eines Rechtecks das Produkt seiner beiden benachbarten Seitenlängen.

Wenn eine Figur von einer beliebig geformten Kurve begrenzt wird, die der Graph einer Funktion ist, kann man ihren Flächeninhalt mithilfe der Integralrechnung berechnen.

Der Flächeninhalt einer zusammengesetzten Figur ergibt sich aus der Summe der Einzelflächen.

Die Analytische Geometrie bietet weitere Möglichkeiten zur Bestimmung von Flächeninhalten. Zum Beispiel ist die Fläche eines Parallelogramms der Betrag des Kreuzprodukts der beiden Vektoren, die es aufspannen.

Zusammenfassung

Der Flächeninhalt ist ein Maß für die Größe eines zweidimensionalen Objekts oder einer Figur. Er wird in Quadratmetern (m²) angegeben, kann aber auch in anderen Längeneinheiten quadriert werden. Es gibt verschiedene Methoden zur Berechnung des Flächeninhalts, wie zum Beispiel Formeln für einfache Figuren, die Verwendung der Integralrechnung oder die Anwendung analytischer geometrischer Konzepte. Der Flächeninhalt einer zusammengesetzten Figur ergibt sich aus der Summe der Einzelflächen.

Alles, was Sie über den Flächeninhalt wissen müssen

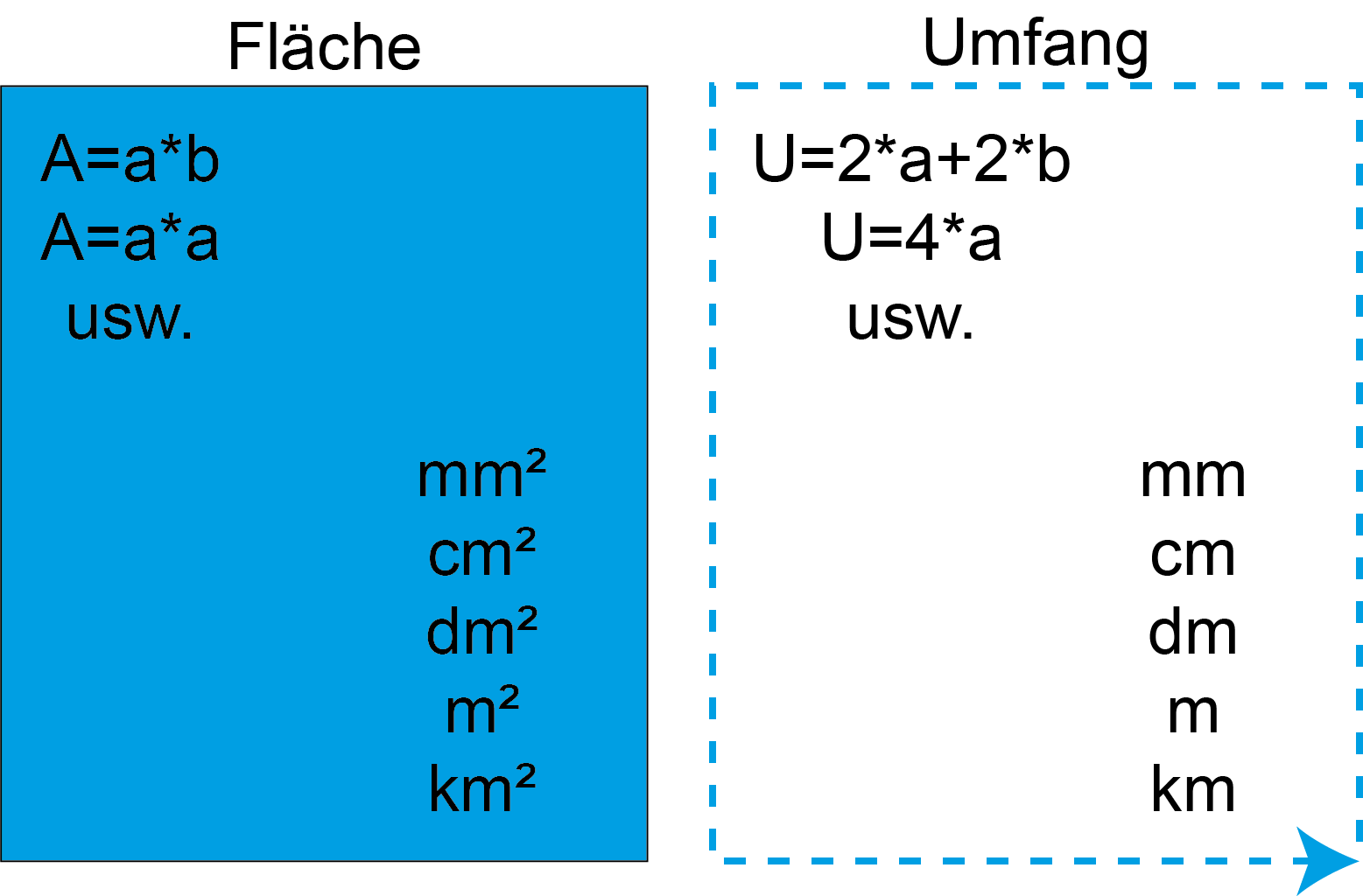
Flächeninhalt als Maß für die Größe von zweidimensionalen Objekten

Der Flächeninhalt ist ein Maß für die Größe eines zweidimensionalen Objekts oder einer Figur. Er gibt an, wie viel Fläche das Objekt einnimmt. Der Flächeninhalt wird oft einfach als „Fläche“ bezeichnet, was jedoch zu Missverständnissen führen kann, da dieser Begriff sowohl das Objekt selbst als auch seine Größe umfassen kann. Zum Beispiel kann man sagen „diese Fläche malen wir grün an“, um auf das Objekt selbst zu verweisen, oder „die Fläche des Ackers beträgt einen halben Hektar“, um auf die Größe des Objekts hinzuweisen.

Im dreidimensionalen Raum spricht man meist von der „Oberfläche“ eines Körpers, wenn man über Flächen spricht. Genauer gesagt bezieht sich der Begriff „Oberflächeninhalt“ auf den Flächeninhalt eines Körpers. Die Basiseinheit des Flächeninhalts ist der Quadratmeter (m²), aber prinzipiell kann jede andere Längeneinheit quadriert werden, um eine Flächeneinheit zu erhalten. Zum Beispiel sind 100 Meter mal 100 Meter ein Hektar und (1 cm)² sind ein Quadratzentimeter.

Berechnung des Flächeninhalts

Für viele Figuren gibt es einfache Formeln zur Berechnung ihres Flächeninhalts. Zum Beispiel ist die Fläche eines Rechtecks das Produkt seiner beiden benachbarten Seitenlängen. Wenn eine Figur von einer beliebig geformten Kurve begrenzt wird, die der Graph einer Funktion ist, kann man ihren Flächeninhalt mithilfe der Integralrechnung berechnen. Der Flächeninhalt einer zusammengesetzten Figur ergibt sich aus der Summe der Einzelflächen.

Die Analytische Geometrie bietet weitere Möglichkeiten zur Bestimmung von Flächeninhalten. Zum Beispiel entspricht die Fläche eines Parallelogramms dem Betrag des Kreuzprodukts (Vektorprodukts) der beiden Vektoren, die es aufspannen. Das Volumen eines Parallelepipeds entspricht dem Betrag des Spatprodukts der drei es aufspannenden Vektoren.

Achsensymmetrie

Achsensymmetrie bezieht sich auf die Eigenschaft einer Figur, dass sie spiegelsymmetrisch zur Achse ist. Das bedeutet, dass es eine Achse gibt, entlang derer die Figur gespiegelt werden kann und dabei unverändert bleibt. Diese Achse wird als Spiegelachse bezeichnet und ein Punkt auf dieser Achse als Spiegelpunkt. Eine Figur wird als achsensymmetrisch oder punktsymmetrisch bezeichnet, wenn sie mindestens einen Spiegelpunkt hat und ihre Form unverändert bleibt, wenn sie um diesen Punkt gespiegelt wird.

Ähnlichkeit

Ähnlichkeit bezieht sich auf die Eigenschaft zweier Figuren, dass sie in ihrer Form gleich sind, aber unterschiedliche Größen haben können. Eine Ähnlichkeitsabbildung ist eine Transformation, die eine Figur in eine ähnliche Figur überführt. Dabei bleiben die Winkel zwischen den Seiten erhalten, aber die Seitenlängen können sich ändern. Ähnlichkeit wird oft verwendet, um Verhältnisse zwischen verschiedenen Größen darzustellen.

Eine Figur kann als ähnlich bezeichnet werden, wenn sie die gleichen Innenwinkel hat wie eine andere Figur und die Verhältnisse der Seitenlängen gleich sind. Ähnlichkeit ist ein wichtiges Konzept in der Geometrie und wird unter anderem bei der Konstruktion von Modellen oder bei der Berechnung von Skalierungen verwendet.

Flächeninhalt erklärt: Definition und Beispiele

Definition des Flächeninhalts

Der Flächeninhalt ist ein Maß für die Größe eines zweidimensionalen Objekts oder einer Figur. Er gibt an, wie viel Fläche eine bestimmte Figur einnimmt. Der Flächeninhalt wird oft auch einfach nur als „Fläche“ bezeichnet, was jedoch missverständlich sein kann, da dieser Begriff sowohl das Objekt selbst als auch seine Größe umfassen kann. Im dreidimensionalen Raum spricht man meist von der „Oberfläche“ eines Körpers.

Die Basiseinheit des Flächeninhalts ist der Quadratmeter (m²). Es ist jedoch möglich, jede andere Längeneinheit zu quadrieren, um eine Flächeneinheit zu erhalten. Zum Beispiel entspricht 100 Meter mal 100 Meter einem Hektar und (1 cm)² einem Quadratzentimeter.

Berechnung des Flächeninhalts

Für viele Figuren gibt es einfache Formeln zur Berechnung des Flächeninhalts. So ist zum Beispiel die Fläche eines Rechtecks das Produkt seiner beiden benachbarten Seitenlängen.

Wenn eine Figur von einer beliebig geformten Kurve begrenzt wird, die der Graph einer Funktion ist, kann man ihren Flächeninhalt mithilfe der Integralrechnung berechnen.

Der Flächeninhalt einer zusammengesetzten Figur ergibt sich aus der Summe der Einzelflächen.

In der Analytischen Geometrie gibt es weitere Möglichkeiten zur Bestimmung von Flächeninhalten. Zum Beispiel ist die Fläche eines Parallelogramms der Betrag des Kreuzprodukts der beiden Vektoren, die es aufspannen.

Beispiele für Flächeninhalte

– Die Fläche eines Quadrats mit einer Seitenlänge von 5 Metern beträgt 25 Quadratmeter.
– Die Fläche eines Rechtecks mit einer Länge von 6 Metern und einer Breite von 4 Metern beträgt 24 Quadratmeter.
– Die Fläche eines Kreises mit einem Radius von 3 Metern beträgt etwa 28,27 Quadratmeter.
– Die Fläche eines Dreiecks mit einer Basislänge von 8 Metern und einer Höhe von 6 Metern beträgt 24 Quadratmeter.

Diese Beispiele zeigen, wie der Flächeninhalt verschiedener Figuren berechnet werden kann. Es ist wichtig zu beachten, dass die Einheiten der Seitenlängen oder Radien in derselben Einheit angegeben sein müssen, um den korrekten Flächeninhalt zu erhalten.

Grundlagen des Flächeninhalts: Definition und Formeln

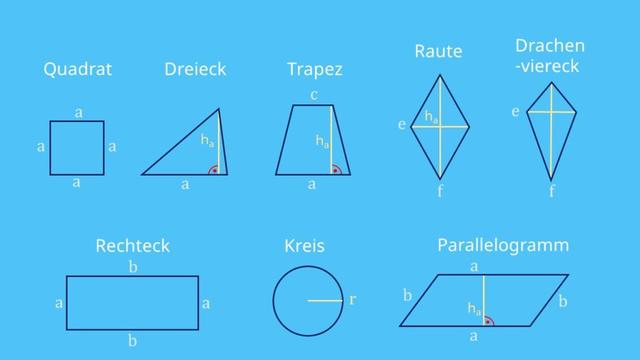
Definition des Flächeninhalts

Der Flächeninhalt ist ein Maß für die Größe eines zweidimensionalen Objekts oder einer Figur. Er gibt an, wie viel Fläche das Objekt einnimmt. Der Begriff „Fläche“ wird oft synonym verwendet, kann jedoch zu Missverständnissen führen, da er sowohl das Objekt selbst als auch seine Größe bezeichnen kann. Beispielsweise kann man sagen „diese Fläche malen wir grün an“ oder „die Fläche des Ackers beträgt einen halben Hektar“.

Einheit des Flächeninhalts

Die Basiseinheit des Flächeninhalts ist der Quadratmeter (m²). Es ist jedoch möglich, jede andere Längeneinheit zu quadrieren, um eine Flächeneinheit zu erhalten. Zum Beispiel entspricht 100 Meter mal 100 Meter einem Hektar und (1 Zentimeter)² einem Quadratzentimeter.

Berechnung des Flächeninhalts

Für viele Figuren gibt es einfache Formeln zur Berechnung des Flächeninhalts. So ist zum Beispiel die Fläche eines Rechtecks das Produkt seiner beiden benachbarten Seitenlängen.

Wenn eine Figur von einer beliebig geformten Kurve begrenzt wird, die der Graph einer Funktion ist, kann man ihren Flächeninhalt mithilfe der Integralrechnung berechnen.

Der Flächeninhalt einer zusammengesetzten Figur ergibt sich aus der Summe der Einzelflächen.

Die Analytische Geometrie bietet weitere Möglichkeiten zur Bestimmung von Flächeninhalten. Zum Beispiel entspricht die Fläche eines Parallelogramms dem Betrag des Kreuzprodukts (Vektorprodukts) der beiden Vektoren, die es aufspannen.

Zusammenfassung

Der Flächeninhalt ist ein Maß für die Größe eines zweidimensionalen Objekts oder einer Figur. Er wird in Quadratmetern gemessen, kann aber auch in anderen Längeneinheiten quadriert werden. Es gibt verschiedene Formeln zur Berechnung des Flächeninhalts, abhängig von der Form der Figur. Bei zusammengesetzten Figuren ergibt sich der Flächeninhalt aus der Summe der Einzelflächen. In der Analytischen Geometrie können weitere Methoden zur Bestimmung von Flächeninhalten verwendet werden, wie das Kreuzprodukt bei Parallelogrammen.

Der Flächeninhalt ist ein Maß für die Größe einer geometrischen Figur in der Ebene. Er wird berechnet, indem man die Fläche dieser Figur bestimmt. Der Flächeninhalt ist eine wichtige Größe in der Mathematik und findet Anwendung in verschiedenen Bereichen wie zum Beispiel der Geometrie oder der Physik. Durch das Verständnis des Flächeninhalts können wir Formen vergleichen, Bereiche messen und komplexe Probleme lösen.