Sattelpunkte: Definition und Berechnung einfach erklärt

Ein Sattelpunkt ist ein wichtiger Begriff in der Mathematik, insbesondere in der Differentialrechnung. Er bezeichnet einen kritischen Punkt auf einer Funktion, an dem die Krümmung sowohl in horizontaler als auch in vertikaler Richtung wechselt. In diesem kurzen Artikel werden wir genauer erklären, was ein Sattelpunkt ist und wie er mathematisch definiert wird.

Was ist ein Sattelpunkt und wie berechnet man ihn?

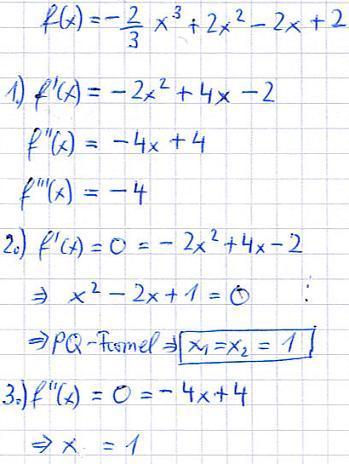
Ein Sattelpunkt ist ein Punkt auf dem Graphen einer Funktion, an dem die Funktion eine Steigung von 0 hat und sowohl davor als auch danach fällt oder steigt. Es handelt sich um einen Wendepunkt mit waagerechter Tangente.

Um einen Sattelpunkt zu berechnen, müssen bestimmte Bedingungen erfüllt sein. Zunächst werden die ersten drei Ableitungen der Funktion berechnet. Dann werden die Nullstellen der zweiten Ableitung ermittelt und in die dritte Ableitung eingesetzt. Wenn dabei Werte ungleich 0 erhalten werden, handelt es sich um Wendepunkte.

Anschließend werden die Wendepunkte in die erste Ableitung eingesetzt. Wenn dabei ein Wert von 0 herauskommt, liegt an dieser Stelle ein Sattelpunkt vor.

Um die genauen Koordinaten des Sattelpunktes zu bestimmen, werden die x-Werte aus Schritt 4 in die Funktion eingesetzt, um die entsprechenden y-Koordinaten zu erhalten.

Es ist wichtig zu beachten, dass ein Sattelpunkt eine Änderung des Krümmungsverhaltens der Funktion darstellt. Vor dem Sattelpunkt ist die Funktion linksgekrümmt, während sie nach dem Sattelpunkt rechtsgekrümmt ist.

Die Berechnung eines Sattelpunktes erfolgt also durch das Überprüfen der Bedingungen für einen Wendepunkt und zusätzlich das Überprüfen der Steigung an den Wendepunkten.

Es gibt auch Fälle, in denen bestimmte Funktionen trotz einer dritten Ableitung von 0 einen Sattelpunkt haben können. In solchen Fällen werden x-Werte links und rechts von der kritischen Stelle in die zweite Ableitung eingesetzt. Wenn dabei ein positiver und ein negativer Wert erhalten werden, handelt es sich um einen Sattelpunkt.

Zusammenfassend kann gesagt werden, dass ein Sattelpunkt ein spezieller Wendepunkt mit waagerechter Tangente ist, bei dem sowohl die Krümmung als auch die Steigung bestimmte Bedingungen erfüllen müssen.

Schritt-für-Schritt Anleitung: Wie berechnet man einen Sattelpunkt?

Schritt 1: Berechne die ersten drei Ableitungen der Funktion f(x).

– Bestimme die Ableitungen von f(x) nach x.
– Berechne die erste Ableitung f'(x).
– Berechne die zweite Ableitung f“(x).
– Berechne die dritte Ableitung f“'(x).

Schritt 2: Ermittle die Nullstellen der zweiten Ableitung.

– Setze f“(x) = 0 und löse nach x auf.
– Die gefundenen x-Werte sind potenzielle Wendepunkte.

Schritt 3: Setze die Nullstellen der zweiten Ableitung in die dritte Ableitung ein.

– Setze die gefundenen x-Werte in f“'(x) ein.
– Wenn f“'(x) ≠ 0 ist, handelt es sich um Wendepunkte.

Schritt 4: Setze die Wendepunkte in die erste Ableitung ein.

– Setze die gefundenen x-Werte in f'(x) ein.
– Wenn f'(x) = 0 ist, handelt es sich um Sattelpunkte.

Schritt 5: Bestimme die y-Koordinaten der Sattelpunkte.

– Setze die gefundenen x-Werte in f(x) ein, um die entsprechenden y-Koordinaten zu erhalten.

Nun kannst du Schritt für Schritt vorgehen, um einen Sattelpunkt einer Funktion zu berechnen. Beachte, dass dies eine allgemeine Anleitung ist und je nach Funktion unterschiedliche Schritte erforderlich sein können.

Sattelpunkte einer gebrochenrationalen Funktion: Schritt-für-Schritt Anleitung

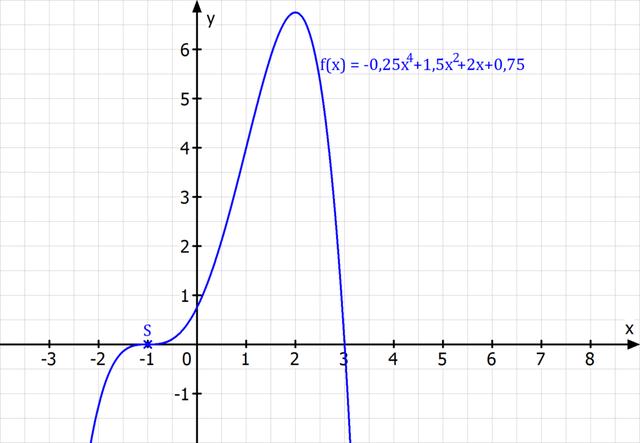
Was sind Sattelpunkte?

Ein Sattelpunkt oder Terrassenpunkt ist ein Punkt auf dem Graphen einer Funktion, an dem die Funktion eine Steigung von 0 hat und der Graph sowohl davor als auch danach fällt oder steigt. Ein Sattelpunkt ist also ein Wendepunkt mit einer waagerechten Tangente.

Wie berechnet man Sattelpunkte?

Um einen Sattelpunkt zu berechnen, muss man die folgenden Schritte durchführen:

1. Berechne die ersten drei Ableitungen der Funktion.
2. Ermittle die Nullstellen der zweiten Ableitung.
3. Setze die Nullstellen der zweiten Ableitung in die dritte Ableitung ein. Wenn dabei Werte ungleich 0 herauskommen, handelt es sich um Wendepunkte.
4. Setze die Wendepunkte in die erste Ableitung ein. Wenn dabei Werte gleich 0 herauskommen, handelt es sich um Sattelpunkte.
5. Setze die x-Werte aus Schritt 4 in die Funktion ein, um die y-Koordinaten der Sattelpunkte zu bestimmen.

Beispiel

Nehmen wir an, wir haben eine gebrochenrationale Funktion f(x) gegeben und möchten den Sattelpunkt berechnen.

1. Wir berechnen zunächst die Ableitungen der Funktion f(x).
2. Danach ermitteln wir die Nullstellen der zweiten Ableitung.
3. Wir setzen diese Nullstellen in die dritte Ableitung ein und erhalten Ergebnisse ungleich 0, also handelt es sich um Wendepunkte.
4. Wir setzen die Wendepunkte in die erste Ableitung ein und erhalten Ergebnisse gleich 0, also handelt es sich um Sattelpunkte.
5. Abschließend setzen wir die x-Werte der Sattelpunkte in die Funktion f(x) ein, um die y-Koordinaten zu bestimmen.

Wendepunkt oder Sattelpunkt?

Um zu überprüfen, ob es sich bei einem Wendepunkt tatsächlich um einen Sattelpunkt handelt, muss man zusätzlich die Steigung an dieser Stelle überprüfen. Wenn die Steigung gleich 0 ist, handelt es sich um einen Sattelpunkt.

Sattelpunkt berechnen: Anleitung und Beispiele

Ein Sattelpunkt ist ein Punkt auf einem Funktionsgraphen, an dem die Funktion eine Steigung von 0 hat und der Graph sowohl davor als auch danach fällt oder steigt. Es handelt sich also um einen Wendepunkt mit einer waagerechten Tangente.

Um den Sattelpunkt einer Funktion zu berechnen, gibt es verschiedene Schritte:

1. Berechne die ersten drei Ableitungen der Funktion f(x).
2. Ermittle die Nullstellen der zweiten Ableitung.
3. Setze die Nullstellen der zweiten Ableitung in die dritte Ableitung ein. Wenn dabei 0 herauskommt, handelt es sich um Wendestellen.
4. Setze die Wendestellen in die erste Ableitung ein. Wenn dabei 0 herauskommt, hat f an dieser Stelle einen Sattelpunkt.
5. Setze die x-Werte aus Schritt 4 in die Funktion f(x) ein, um die y-Koordinaten des Sattelpunktes zu bestimmen.

Hier ist ein konkretes Beispiel zur Verdeutlichung:

Angenommen wir haben die Funktion f(x) = x^3 – 3x^2 + 2x + 1.

Schritt 1: Berechne die Ableitungen von f(x):
f'(x) = 3x^2 – 6x + 2
f“(x) = 6x – 6
f“'(x) = 6

Schritt 2: Ermittle die Nullstellen der zweiten Ableitung:
Setze f“(x) = 0 und löse nach x auf:
6x – 6 = 0
x = 1

Schritt 3: Setze die ermittelte Nullstelle in die dritte Ableitung ein:
f“'(1) = 6
Da der Wert ungleich 0 ist, handelt es sich um eine Wendestelle.

Schritt 4: Überprüfe, ob es sich bei der Wendestelle um einen Sattelpunkt handelt:
Setze x = 1 in die erste Ableitung f'(x) ein:
f'(1) = 3 – 6 + 2
f'(1) = -1
Da der Wert ungleich 0 ist, handelt es sich nicht um einen Sattelpunkt.

Schritt 5: Berechne die y-Koordinate des Wendepunktes:
Setze x = 1 in die Funktion f(x) ein:
f(1) = (1)^3 – 3(1)^2 + 2(1) + 1
f(1) = 2

Der berechnete Wendepunkt hat also die Koordinaten (1,2).

Das war eine Anleitung zur Berechnung von Sattelpunkten einer Funktion. Es ist wichtig zu beachten, dass Sattelpunkte spezielle Wendepunkte sind und daher zusätzliche Bedingungen erfüllen müssen.

Alles über Sattelpunkte: Definition und Berechnung

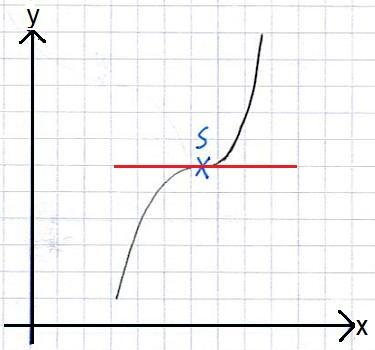
Definition

Ein Sattelpunkt, auch Terrassenpunkt genannt, ist ein Punkt auf dem Graphen einer Funktion, an dem die Steigung der Funktion 0 ist. Vor und nach dem Sattelpunkt fällt bzw. steigt der Graph.

Berechnung

Um einen Sattelpunkt zu berechnen, müssen bestimmte Bedingungen erfüllt sein:
1. Die erste Ableitung der Funktion muss an der Stelle des Sattelpunktes gleich 0 sein.
2. Die zweite Ableitung der Funktion muss an der Stelle des Sattelpunktes ungleich 0 sein.
3. Die dritte Ableitung der Funktion muss an den Wendepunkten (Nullstellen der zweiten Ableitung) ungleich 0 sein.

Um die Koordinaten des Sattelpunktes zu bestimmen, setzt man die x-Werte aus Schritt 4 in die Funktion ein und erhält die entsprechenden y-Koordinaten.

Es ist wichtig zu beachten, dass ein Wendepunkt nicht automatisch ein Sattelpunkt ist. Für einen Sattelpunkt müssen zusätzlich die oben genannten Bedingungen erfüllt sein.

Beispielhaft wird dies im Artikel mit konkreten Aufgaben und Lösungen erklärt. Es wird auch darauf hingewiesen, dass es bestimmte Funktionen geben kann, bei denen trotz Erfüllung aller Bedingungen kein Sattelpunkt vorliegt.

Zusätzlich wird erwähnt, dass man mithilfe dieser Informationen auch die Wendetangente berechnen kann, welche eine lineare Funktion ist, die den Graphen am Wendepunkt berührt.

Wie bestimmt man einen Sattelpunkt in der Mathematik?

Ein Sattelpunkt in der Mathematik ist ein Punkt auf dem Graphen einer Funktion, an dem die Funktion eine waagerechte Tangente hat und sowohl davor als auch danach fällt oder steigt. Um einen Sattelpunkt zu bestimmen, kann man folgende Schritte befolgen:

1. Berechne die ersten drei Ableitungen der Funktion f(x).
– Die Ableitungen geben uns Informationen über die Steigung und das Krümmungsverhalten der Funktion.

2. Ermittle die Nullstellen der zweiten Ableitung.
– Die Nullstellen der zweiten Ableitung geben uns mögliche Wendepunkte.

3. Setze die Nullstellen der zweiten Ableitung in die dritte Ableitung ein.
– Wenn die dritte Ableitung an den Wendepunkten ungleich null ist, handelt es sich um Terrassenpunkte.

4. Setze die Wendepunkte in die erste Ableitung ein.
– Wenn die erste Ableitung an den Wendepunkten gleich null ist, handelt es sich um Sattelpunkte.

5. Bestimme die y-Koordinaten der Sattelpunkte, indem du die x-Werte aus Schritt 4 in die Funktion f(x) einsetzt.

Es ist wichtig zu beachten, dass diese Schritte hinreichend aber nicht notwendig sind, um einen Sattelpunkt zu bestimmen. Es gibt bestimmte Funktionen, bei denen trotz einer dritten Ableitung von null ein Sattelpunkt existieren kann. In solchen Fällen kann man zusätzlich x-Werte links und rechts von der kritischen Stelle in die zweite Ableitung einsetzen und prüfen, ob ein Wert positiv und der andere negativ ist.

Die Berechnung von Sattelpunkten kann in der Kurvendiskussion von Funktionen hilfreich sein, um das Krümmungsverhalten des Graphen zu analysieren.

Ein Sattelpunkt ist ein Punkt auf einer Funktion, an dem die Krümmung wechselt. Es handelt sich um einen kritischen Punkt, der weder ein Maximum noch ein Minimum ist. Sattelpunkte spielen eine wichtige Rolle in der Differentialrechnung und können zur Analyse von Kurvenverläufen verwendet werden.