Irrationale Zahlen sind eine faszinierende und geheimnisvolle mathematische Konzept. Sie können nicht als Bruch zweier ganzer Zahlen dargestellt werden und haben unendlich viele nicht periodische Dezimalstellen. Ihre Existenz wurde von antiken Mathematikern entdeckt und hat unsere Vorstellung von Zahlen erweitert. In diesem Artikel werden wir uns genauer mit irrationalen Zahlen befassen und ihre Eigenschaften sowie ihre Bedeutung in der Mathematik diskutieren.
Eine Einführung in irrationale Zahlen: Definition und Eigenschaften
Definition der irrationalen Zahlen
Die irrationalen Zahlen sind alle Zahlen, die sich nicht als Quotient oder Verhältnis aus zwei ganzen Zahlen schreiben lassen. Anders ausgedrückt gehören sie nicht zur Menge der rationalen Zahlen \(\mathbb Q\). Die Menge der irrationalen und rationalen Zahlen zusammen bildet die Menge der reellen Zahlen \(\mathbb R\).
Eigenschaften der irrationalen Zahlen
1. Darstellung als Dezimalzahlen: Eine wichtige Eigenschaft irrationaler Zahlen ist, dass sie sich als Dezimalzahlen weder abbrechen noch periodisch wiederholen. Dies bedeutet, dass es unendlich viele Nachkommastellen gibt, ohne dass ein bestimmtes Muster erkennbar ist.
2. Unendlich viele irrationale Zahlen: Es gibt unendlich viele irrationale Zahlen auf der Zahlengeraden. Selbst zwischen zwei beliebigen rationalen Zahlen existieren immer noch unendlich viele irrationale Zahlen.
3. Beispiel des Beweises für die Irrationalität von \(\sqrt 2\): Ein bekanntes Beispiel für einen Beweis zur Irrationalität einer Zahl ist der Beweis für die Irrationalität von \(\sqrt 2\). Durch einen indirekten Beweis wird gezeigt, dass es keine natürlichen Zahlen \(r\) und \(s\) geben kann, deren Verhältnis gleich \(\sqrt 2\) ist.
Diese Eigenschaften machen die irrationalen Zahlen zu einer interessanten und vielfältigen Menge innerhalb der reellen Zahlen.
Irrationale Zahlen erklärt: Warum können sie nicht als Brüche geschrieben werden?
Was sind rationale und irrationale Zahlen?
Rationale Zahlen sind alle Zahlen, die sich als Quotient oder Verhältnis zweier ganzer Zahlen schreiben lassen. Sie gehören zur Menge der rationalen Zahlen \(\mathbb Q\). Irrationale Zahlen hingegen können nicht als solche Quotienten geschrieben werden und gehören daher nicht zur Menge \(\mathbb Q\). Die irrationalen und die rationalen Zahlen bilden zusammen die Menge der reellen Zahlen \(\mathbb R\).
Die Darstellung von irrationalen Zahlen
Der Unterschied zwischen rationalen und irrationalen Zahlen wird deutlich, wenn man sie als Dezimalzahlen darstellt. Irrationale Zahlen haben unendlich viele Nachkommastellen, die weder abbrechen noch periodisch sind. Im Gegensatz dazu haben rationale Zahlen entweder eine endliche Anzahl an Nachkommastellen oder eine wiederkehrende Periodizität.
Es gibt unendlich viele irrationale Zahlen auf der Zahlengeraden und sogar zwischen zwei beliebigen rationalen Zahlen liegen immer noch unendlich viele irrationale Zahlen.
Der Beweis für die Irrationalität von \(\sqrt 2\)
Ein Beispiel für einen Beweis der Irrationalität einer Zahl ist der Beweis für die Irrationalität von \(\sqrt 2\). Man nimmt zunächst an, dass \(\sqrt 2\) eine rationale Zahl ist und schreibt sie als Bruch \(\frac{r}{s}\) mit zwei teilerfremden natürlichen Zahlen r und s.
Durch Umformungen zeigt man dann, dass dies zu einem Widerspruch führt. Man kommt zu dem Schluss, dass weder r noch s gerade sein können, obwohl sie als teilerfremd angenommen wurden.
Aus diesem Beweis folgt, dass \(\sqrt 2\) keine rationale Zahl ist und somit zu den irrationalen Zahlen gehört.
Die irrationalen Zahlen sind also eine wichtige Ergänzung zu den rationalen Zahlen und tragen zur Vollständigkeit der Menge der reellen Zahlen bei.
Der Unterschied zwischen rationalen und irrationalen Zahlen: Eine Übersicht
Rationale Zahlen:
– Rationale Zahlen sind alle Zahlen, die sich als Bruch aus zwei ganzen Zahlen darstellen lassen.
– Sie gehören zur Menge der rationalen Zahlen \(\mathbb Q\).
– Beispiele für rationale Zahlen sind \(\frac{1}{2}\), \(\frac{3}{4}\) und \(-\frac{5}{8}\).
– Rationale Zahlen können als endliche oder periodische Dezimalzahlen dargestellt werden.
Irrationale Zahlen:
– Irrationale Zahlen sind alle Zahlen, die sich nicht als Bruch aus zwei ganzen Zahlen darstellen lassen.
– Sie gehören nicht zur Menge der rationalen Zahlen \(\mathbb Q\), sondern zur Menge der reellen Zahlen \(\mathbb R\).
– Beispiele für irrationale Zahlen sind \(\sqrt{2}\), \(\pi\) und \(e\).
– Irrationale Zahlen können als weder abbrechende noch periodische Dezimalzahlen dargestellt werden.
– Zwischen zwei beliebigen rationalen Zahlen liegen unendlich viele irrationale Zahlen.
Beweis für die Irrationalität von \(\sqrt{2}\):
Um zu zeigen, dass die Zahl \(\sqrt{2}\) irrational ist, nehmen wir an, dass sie rational ist (\(r^2 = 2s^2\) mit \(r\) und \(s\) als teilerfremde natürliche Zahlen). Durch einen indirekten Beweis zeigen wir dann, dass dies nicht stimmen kann. Da \(r\) und \(s\) beide gerade sein müssten, wären sie nicht teilerfremd, was im Widerspruch zur Annahme steht. Daher kann es keine zwei natürlichen Zahlen geben, deren Verhältnis gleich \(\sqrt{2}\) ist.
Die Unterscheidung zwischen rationalen und irrationalen Zahlen ist wichtig in der Mathematik und hat viele Anwendungen, zum Beispiel in der Geometrie und Analysis.
Die Bedeutung irrationaler Zahlen in der Mathematik: Ein Überblick
Definition und Eigenschaften irrationaler Zahlen
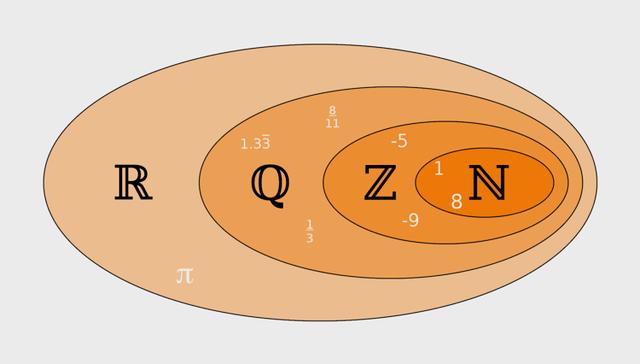
Die irrationalen Zahlen sind eine wichtige Klasse von Zahlen in der Mathematik. Sie werden definiert als alle Zahlen, die sich nicht als Quotient oder Verhältnis zweier ganzer Zahlen darstellen lassen. Anders ausgedrückt gehören sie nicht zur Menge der rationalen Zahlen \(\mathbb Q\). Die rationalen und irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen \(\mathbb R\). Eine mögliche Schreibweise für die Menge der irrationalen Zahlen ist \(\mathbb R \setminus \mathbb Q\).
Der Unterschied zwischen rationalen und irrationalen Zahlen zeigt sich in ihrer Darstellung als Dezimalzahlen. Während rationale Zahlen entweder endliche oder periodische Dezimalbrüche sind, haben irrationale Zahlen unendlich viele nicht-periodische Nachkommastellen. Es gibt unendlich viele verschiedene irrationale Zahlen und zwischen zwei beliebigen rationalen Zahlen liegen immer noch unendlich viele irrationale Zahlen auf der Zahlengeraden.
Anwendung und Bedeutung irrationaler Zahlen
Irrationale Zahlen spielen eine wichtige Rolle in verschiedenen mathematischen Disziplinen. In der Geometrie treten sie beispielsweise bei der Konstruktion des goldenen Schnitts auf, welcher ein Verhältnis ist, das durch eine irrationale Zahl beschrieben wird. Auch bei der Berechnung von Längen, Flächeninhalten oder Volumina von geometrischen Figuren können irrationalen Zahlen auftreten.
In der Analysis werden irrationale Zahlen zur Untersuchung von Grenzwerten und Konvergenz verwendet. Sie sind unverzichtbar bei der Definition und Analyse von Funktionen, Ableitungen und Integralen. Die Eigenschaften irrationaler Zahlen ermöglichen es Mathematikern, komplexe mathematische Probleme zu lösen und wichtige Zusammenhänge in der Natur oder Wissenschaft zu beschreiben.
Die Bedeutung irrationaler Zahlen geht jedoch über die Mathematik hinaus. Sie haben auch philosophische Implikationen, da sie aufzeigen, dass es im Universum unendlich viele nicht-rational erklärbare Phänomene gibt. Irrationale Zahlen fordern unser Verständnis von Realität und Rationalität heraus und zeigen uns die Grenzen unserer Vorstellungskraft auf.
Der Beweis für die Irrationalität der Zahl √2: Ein grundlegendes Konzept erklärt
Einleitung
Der Beweis für die Irrationalität der Zahl √2 ist ein klassisches Beispiel dafür, wie man mit Hilfe eines indirekten Beweises zu einem fundamentalen Ergebnis gelangen kann. Dieser Beweis zeigt, dass √2 keine rationale Zahl ist und daher zu den irrationalen Zahlen gehört.
Der indirekte Beweis
Um zu beweisen, dass √2 irrational ist, nehmen wir zunächst an, dass es eine rationale Zahl r gibt, deren Quadrat 2 ergibt. Das bedeutet, dass √2 = r/s gilt, wobei r und s teilerfremde natürliche Zahlen sind.
Durch Umformungen können wir zeigen, dass in diesem Fall sowohl r als auch s gerade Zahlen sein müssen. Angenommen r ist gerade, dann existiert eine natürliche Zahl n, sodass r = 2n. Damit ergibt sich (2n)^2 = 4n^2 = 2s^2. Durch weitere Umformungen erhalten wir 2n^2 = s^2.
Da s^2 ebenfalls gerade sein muss, folgt daraus, dass auch s gerade sein muss. Dies widerspricht jedoch unserer Annahme, dass r und s teilerfremd sind.
Folglich kann es keine rationalen Zahlen geben, deren Verhältnis gleich √2 ist. Somit ist √2 irrational.
Zusammenfassung
Der Beweis für die Irrationalität der Zahl √2 basiert auf einem indirekten Beweisverfahren. Durch Annahme des Gegenteils und anschließende logische Umformungen kann gezeigt werden, dass es keine rationale Zahl gibt, deren Quadrat 2 ergibt. Somit gehört √2 zu den irrationalen Zahlen. Dieser Beweis verdeutlicht das grundlegende Konzept der Irrationalität und zeigt, wie man mit relativ einfachen Gedankengängen zu fundamentalen mathematischen Erkenntnissen gelangen kann.
Unendlich viele irrationale Zahlen: Eine Entdeckungsreise durch die Dezimalzahlen
Was sind irrationalen Zahlen?
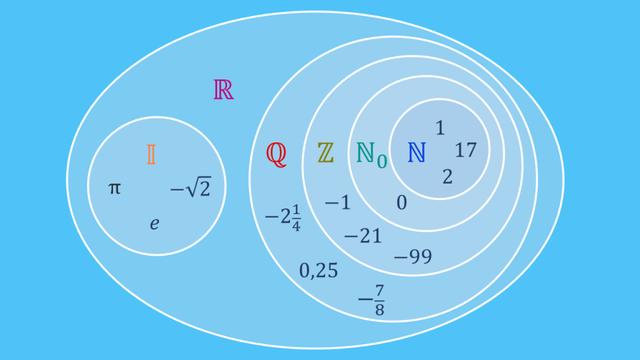
Die irrationalen Zahlen sind eine Teilmenge der reellen Zahlen, die sich nicht als Bruch zweier ganzer Zahlen darstellen lassen. Anders ausgedrückt, sie können nicht als Verhältnis zweier ganzer Zahlen geschrieben werden. Im Gegensatz dazu gehören die rationalen Zahlen zur Menge der reellen Zahlen und können als Bruch dargestellt werden.
Beispiel für eine irrationale Zahl
Ein bekanntes Beispiel für eine irrationale Zahl ist die Wurzel aus 2 (\(\sqrt{2}\)). Der Beweis dafür, dass \(\sqrt{2}\) irrational ist, erfolgt über einen indirekten Beweis. Man nimmt an, dass \(\sqrt{2}\) rational ist und zeigt dann, dass dies zu einem Widerspruch führt. Somit kann \(\sqrt{2}\) keine rationale Zahl sein.
Unendlich viele irrationale Zahlen
Es gibt unendlich viele irrationale Zahlen. Dies lässt sich unter anderem anhand ihrer Darstellung als Dezimalzahlen erkennen. Im Gegensatz zu den rationalen Zahlen gibt es bei den irrationalen Zahlen keine periodischen oder abbrechenden Dezimalstellen. Sie haben eine unendliche Anzahl von Nachkommastellen und können daher nicht in Form eines Bruchs dargestellt werden.
Zwischen zwei beliebigen rationalen Zahlen existieren immer noch unendlich viele irrationale Zahlen auf der Zahlengeraden. Dies verdeutlicht die Vielfalt und Unendlichkeit der irrationalen Zahlen.
Zusammenfassung
Die irrationalen Zahlen sind eine wichtige Teilmenge der reellen Zahlen. Sie können nicht als Verhältnis zweier ganzer Zahlen geschrieben werden und haben unendlich viele Nachkommastellen in ihrer Dezimaldarstellung. Ein bekanntes Beispiel für eine irrationale Zahl ist die Wurzel aus 2 (\(\sqrt{2}\)). Es gibt unendlich viele irrationale Zahlen, die zwischen beliebigen rationalen Zahlen existieren. Diese Vielfalt macht die irrationalen Zahlen zu einem faszinierenden Thema in der Mathematik.
Zusammenfassend sind irrationale Zahlen eine wichtige mathematische Konzept, das uns ermöglicht, die Lücken in der rationalen Zahlensystem zu füllen. Sie können nicht als Brüche dargestellt werden und haben unendlich viele nicht wiederholende Dezimalstellen. Irrationale Zahlen spielen eine bedeutende Rolle in der Geometrie, Physik und anderen Bereichen der Mathematik und tragen zum Verständnis von komplexen mathematischen Konzepten bei.