Wann ist eine Matrix invertierbar? Alles was du darüber wissen musst!

Eine Matrix ist invertierbar, wenn sie eine eindeutige Umkehrmatrix besitzt. Die Invertierbarkeit einer Matrix ist von großer Bedeutung in der linearen Algebra und findet Anwendung in verschiedenen mathematischen Bereichen wie der Lösung linearer Gleichungssysteme oder der Berechnung von Determinanten. In diesem Artikel werden wir uns mit den Kriterien beschäftigen, die erfüllt sein müssen, damit eine Matrix invertierbar ist.

Bedingungen für die Invertierbarkeit einer Matrix

Um festzustellen, ob eine Matrix invertierbar ist, müssen bestimmte Bedingungen erfüllt sein. Hier sind die wichtigsten:

1. Quadratische Matrix: Eine Matrix muss quadratisch sein, um invertierbar zu sein. Das bedeutet, dass sie genauso viele Zeilen wie Spalten haben muss.

2. Determinante ungleich Null: Die Determinante der Matrix darf nicht null sein. Die Determinante ist eine Zahl, die aus den Einträgen der Matrix berechnet wird. Wenn die Determinante null ist, kann die inverse Matrix nicht existieren.

3. Lineare Unabhängigkeit: Die Spalten oder Zeilen einer invertierbaren Matrix müssen linear unabhängig voneinander sein. Das bedeutet, dass keine Spalte oder Zeile als lineare Kombination anderer Spalten oder Zeilen dargestellt werden kann.

4. Vollrangige Matrix: Eine invertierbare Matrix hat den vollen Rang, das heißt, alle ihre Zeilen und Spalten sind linear unabhängig voneinander.

Wenn diese Bedingungen erfüllt sind, kann man davon ausgehen, dass eine Matrix invertierbar ist und eine inverse Matrix existiert. Es ist wichtig zu beachten, dass nicht jede beliebige Matrix invertierbar ist und dass es verschiedene Methoden gibt, um die Inverse einer gegebenen Matrix zu berechnen.

Zusammenfassend können wir sagen, dass eine quadratische Matrix mit einer von Null verschiedenen Determinante und vollrangigen Zeilen und Spalten als invertierbar betrachtet wird.

Erfahren Sie, wann eine Matrix invertierbar ist

Eine Matrix ist invertierbar, wenn sie bestimmte Voraussetzungen erfüllt. Hier sind die Bedingungen, die überprüft werden müssen:

1. Quadratische Matrix: Eine Matrix muss quadratisch sein, das bedeutet, dass die Anzahl der Zeilen und Spalten gleich sein muss. Nur quadratische Matrizen können invertiert werden.

2. Determinante ungleich Null: Die Determinante einer Matrix ist ein Wert, der aus den Einträgen der Matrix berechnet wird. Um zu überprüfen, ob eine Matrix invertierbar ist, muss ihre Determinante ungleich Null sein. Wenn die Determinante Null ist, kann die Matrix nicht invertiert werden.

Es gibt verschiedene Methoden zur Berechnung der Inversen einer Matrix, wie den Gauß-Algorithmus, die Adjunkte oder die Cramersche Regel. Diese Methoden ermöglichen es uns, die inverse Matrix zu berechnen und damit weitere Berechnungen durchzuführen.

Es ist wichtig zu beachten, dass nicht jede beliebige Matrix invertierbar ist. Es gibt singuläre Matrizen, deren Determinante null ist und daher keine inverse Matrix haben. Reguläre Matrizen hingegen sind invertierbar und ermöglichen es uns, mit ihnen zu rechnen.

Zusammenfassend lässt sich sagen, dass eine quadratische Matrix mit einer von Null verschiedenen Determinante als invertierbar betrachtet wird. Die Inverse einer solchen Matrix kann mit verschiedenen Methoden berechnet werden und erlaubt weitere Rechenoperationen mit der ursprünglichen Matrix.

Die Voraussetzungen für eine invertierbare Matrix

Eine Matrix ist invertierbar, wenn sie bestimmte Voraussetzungen erfüllt. Hier sind die wichtigsten Bedingungen:

1. Quadratische Matrix: Eine Matrix muss quadratisch sein, das heißt, sie muss genauso viele Zeilen wie Spalten haben. Nur quadratische Matrizen können invertiert werden.

2. Determinante ungleich Null: Die Determinante einer Matrix muss ungleich Null sein. Die Determinante ist eine Zahl, die aus den Einträgen der Matrix berechnet wird. Ist die Determinante gleich Null, so ist die Matrix nicht invertierbar.

3. Vollständiger Rang: Eine invertierbare Matrix hat immer vollen Rang, das bedeutet, dass alle Zeilen und Spalten linear unabhängig voneinander sind. Wenn eine oder mehrere Zeilen/Spalten linear abhängig sind, kann die Matrix nicht invertiert werden.

Diese Bedingungen stellen sicher, dass die inverse Matrix existiert und eindeutig bestimmt ist. Wenn eine Matrix diese Voraussetzungen erfüllt, dann kann man ihre Inverse berechnen und mit ihr weiter rechnen.

Es ist wichtig zu beachten, dass nicht jede beliebige Matrix invertierbar ist. Es gibt auch singuläre Matrizen, bei denen eine oder mehrere der oben genannten Bedingungen nicht erfüllt sind. Singuläre Matrizen haben keine Inverse und können in gewissen Rechenoperationen problematisch sein.

In unserem Beispiel wurde gezeigt, dass die gegebene Beispielmatrix quadratisch ist und ihre Determinante ungleich Null ist. Daher ist diese Matrix invertierbar und besitzt eine Inverse.

Wann kann man eine Matrix invertieren?

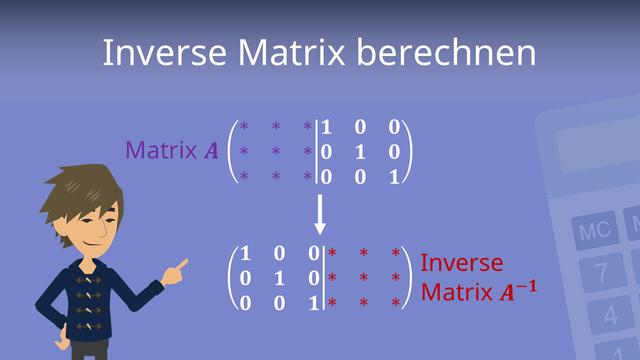
Eine Matrix kann nur dann invertiert werden, wenn sie bestimmte Voraussetzungen erfüllt. Hier sind die Bedingungen, die erfüllt sein müssen:

1. Quadratische Matrix: Eine Matrix muss quadratisch sein, das bedeutet, dass sie genauso viele Zeilen wie Spalten haben muss. Nur quadratische Matrizen können invertiert werden.

2. Determinante ungleich Null: Die Determinante einer Matrix muss ungleich Null sein, damit sie invertierbar ist. Die Determinante ist eine Zahl, die aus den Einträgen der Matrix berechnet wird und gibt Aufschluss über verschiedene Eigenschaften der Matrix. Ist die Determinante gleich Null, so ist die Matrix nicht invertierbar.

Wenn diese beiden Bedingungen erfüllt sind, dann kann die inverse Matrix berechnet werden. Die inverse Matrix ist eine spezielle Art von Matrix, mit der multipliziert man die ursprüngliche Matrix erhält man die Einheitsmatrix.

Es ist wichtig zu beachten, dass nicht alle Matrizen invertierbar sind. Wenn eine Matrix nicht invertierbar ist, nennt man sie singulär.

Zusammenfassend lässt sich sagen, dass eine quadratische Matrix mit einer von Null verschiedenen Determinante invertierbar ist. In unserem Beispiel haben wir gezeigt, dass die gegebene Beispielmatrix diese Bedingungen erfüllt und daher invertierbar ist.

Invertierbarkeit von Matrizen: Was Sie wissen sollten

Die Invertierbarkeit einer Matrix ist ein wichtiges Konzept in der linearen Algebra. Hier sind einige wichtige Informationen, die Sie darüber wissen sollten:

1. Quadratische Matrizen: Eine Matrix muss quadratisch sein, um invertierbar zu sein. Das bedeutet, dass die Anzahl der Zeilen und Spalten gleich sein muss.

2. Determinante ungleich Null: Die Determinante einer Matrix spielt eine entscheidende Rolle bei der Invertierbarkeit. Eine Matrix ist invertierbar, wenn ihre Determinante ungleich Null ist. Wenn die Determinante Null ist, dann ist die Matrix singulär und nicht invertierbar.

3. Berechnung der Inversen: Es gibt verschiedene Methoden zur Berechnung der inversen Matrix, wie den Gauß-Algorithmus, die Adjunkte oder die Cramersche Regel. Diese Methoden ermöglichen es Ihnen, die inverse Matrix zu finden, indem Sie sie mit der ursprünglichen Matrix multiplizieren.

4. Regeln und Eigenschaften: Eine inverse Matrix ist selbst wieder invertierbar. Die Inverse der inversen Matrix ist wieder die ursprüngliche Matrix. Eine inverse Matrix kann auch transponiert werden und das Ergebnis bleibt das gleiche wie bei der Inversion einer transponierten Matrix.

5. Orthogonale Matrizen: Bei orthogonalen Matrizen sind die Inverse und die Transponierte sogar gleich.

Es lohnt sich immer, vorher zu überprüfen, ob eine bestimmte Matrix invertierbar ist, bevor man weitere Berechnungen durchführt.

Wie erkennt man, ob eine Matrix invertierbar ist?

Eine Matrix ist invertierbar, wenn sie bestimmte Voraussetzungen erfüllt. Hier sind einige Kriterien, anhand derer du prüfen kannst, ob eine Matrix invertierbar ist:

1. Quadratische Matrix: Eine Matrix muss quadratisch sein, das bedeutet, dass die Anzahl der Zeilen gleich der Anzahl der Spalten sein muss. Nur quadratische Matrizen können invertiert werden.

2. Determinante ungleich Null: Die Determinante einer Matrix spielt eine wichtige Rolle bei der Invertierbarkeit. Um zu überprüfen, ob eine Matrix invertierbar ist, musst du die Determinante berechnen und sicherstellen, dass sie ungleich Null ist. Wenn die Determinante Null ist, kann die Matrix nicht invertiert werden.

3. Vollrangige Matrix: Eine vollrangige Matrix hat den vollen Rang, das heißt alle ihre Zeilen und Spalten sind linear unabhängig. Wenn eine quadratische Matrix den vollen Rang hat, dann ist sie invertierbar.

4. Singuläre und reguläre Matrizen: Eine singuläre Matrix ist nicht invertierbar und hat eine Determinante von Null. Eine reguläre Matrix hingegen ist invertierbar und hat eine von Null verschiedene Determinante.

Es gibt verschiedene Methoden zur Berechnung der inversen Matrix wie den Gauß-Algorithmus, die Adjunkte oder die Cramersche Regel. Diese Methoden können angewendet werden, um festzustellen, ob eine gegebene quadratische Matrix invertierbar ist.

Es lohnt sich immer vorher zu überprüfen, ob eine Matrix invertierbar ist, bevor du mit ihr rechnest. Dies erspart dir möglicherweise unnötige Berechnungen und ermöglicht es dir, die Eigenschaften der invertierbaren Matrix effizient zu nutzen.

Zusammenfassend lässt sich sagen, dass eine Matrix invertierbar ist, wenn sie quadratisch ist, eine von Null verschiedene Determinante hat und den vollen Rang besitzt. Nur unter diesen Voraussetzungen kann die inverse Matrix berechnet werden.

Insgesamt kann gesagt werden, dass eine Matrix invertierbar ist, wenn sie quadratisch ist und einen vollen Rang hat. Es gibt verschiedene Methoden zur Berechnung der Inversen einer Matrix, wie beispielsweise die Gauß-Jordan-Elimination oder die Determinante. Die Invertierbarkeit einer Matrix spielt eine wichtige Rolle in verschiedenen mathematischen Anwendungen und ermöglicht unter anderem das Lösen von linearen Gleichungssystemen.