Alles über Rhombus: Eigenschaften, Definition und Anwendungen

Ein Rhombus ist eine geometrische Figur, die aus vier gleich langen Seiten besteht und deren gegenüberliegende Winkel gleich sind. In diesem Artikel erfahren Sie alles über die Eigenschaften und Anwendungen eines Rhombus sowie seine Unterschiede zu anderen Vierecken.

Eigenschaften und Definition eines Rhombus

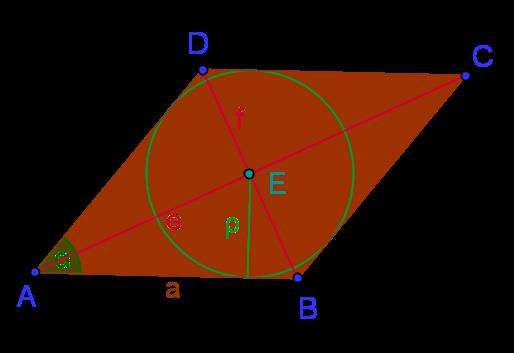
Ein Rhombus, auch bekannt als Raute, ist ein spezielles Viereck, bei dem alle vier Seiten gleich lang sind. Es kann auch als Parallelogramm mit gleich langen Seiten oder als Drachenviereck mit zwei parallelen Seitenpaaren bezeichnet werden.

Ein Rhombus hat einige weitere charakteristische Eigenschaften:

– Ein Rhombus mit einem rechten Winkel in einer seiner Ecken ist ein Quadrat.
– Die gegenüberliegenden Winkel eines Rhombus sind gleich groß.
– Der Flächeninhalt eines Rhombus kann entweder durch das halbe Diagonalenprodukt (\(A = \frac{e \cdot f}{2}\)) oder durch die Formel „Seite mal Höhe“ (\(A = h \cdot a\)) berechnet werden.
– Ein Rhombus besitzt Achsensymmetrie, was bedeutet, dass er um eine Achse gespiegelt werden kann und dabei sein Aussehen nicht verändert.

Zur Veranschaulichung: Wenn ein Blatt DIN-A4-Papier entlang einer bestimmten Strecke gefaltet wird, bleibt das Dreieck fest, während das Viereck in ein neues Viereck übergeht. Dieses neue Viereck liegt wieder in der \(x_1\) – \(x_2\) -Ebene und besitzt die gleichen Eigenschaften wie der ursprüngliche Rhombus.

Es gibt noch weitere mathematische Konzepte und Anwendungen im Zusammenhang mit einem Rhombus, wie zum Beispiel Schnittpunkte von Geraden im Raum oder die Berechnung des Abstands zwischen einem Punkt und einer Ebene. Die genannten Eigenschaften und Definitionen sind jedoch grundlegende Merkmale eines Rhombus.

Merkmale und Bedeutung eines Rhombus

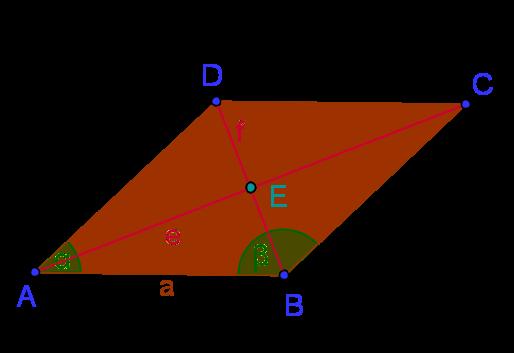
Ein Rhombus, auch bekannt als Raute, ist ein Viereck, bei dem alle vier Seiten gleich lang sind. Es kann auch als Parallelogramm mit gleich langen Seiten oder als Drachenviereck mit zwei parallelen Seitenpaaren bezeichnet werden. Ein besonderes Merkmal einer Raute ist, dass sie einen rechten Winkel haben kann. In diesem Fall wird die Raute zu einem Quadrat.

Der Flächeninhalt eines Rhombus kann auf zwei Arten berechnet werden. Entweder als halbes Diagonalenprodukt oder als „Seite mal Höhe“. Die Achsensymmetrie spielt ebenfalls eine Rolle bei einem Rhombus. Einander gegenüberliegende Winkel sind gleich groß und es gibt eine Spiegelachse, entlang der das Rhombus gespiegelt werden kann.

Die Bedeutung eines Rhombus liegt in seiner geometrischen Eigenschaften und Anwendungen. Aufgrund seiner symmetrischen Form wird es oft in der Kunst und Architektur verwendet. Es hat auch praktische Anwendungen in der Technik und im Bauwesen, wie zum Beispiel bei der Konstruktion von Diamanten oder beim Entwerfen von Fliesenmustern.

Zusammenfassend lässt sich sagen, dass ein Rhombus ein spezielles Viereck mit gleichen Seitenlängen ist und verschiedene geometrische Eigenschaften aufweist. Es hat sowohl ästhetische als auch praktische Anwendungen in verschiedenen Bereichen.

Was zeichnet ein Rhombus aus?

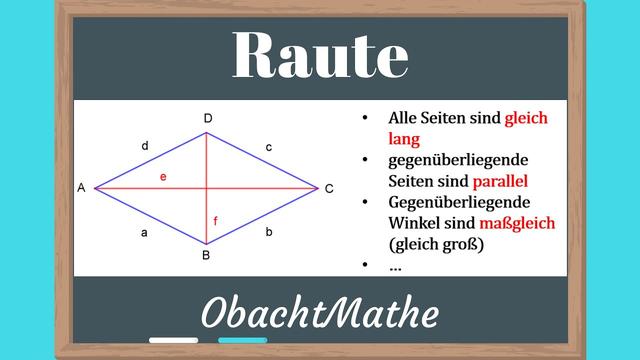
Ein Rhombus, auch als Raute bekannt, ist ein spezielles Viereck, bei dem alle vier Seiten gleich lang sind. Dadurch besitzt er einige besondere Eigenschaften. Ein Rhombus kann auch als Parallelogramm mit gleich langen Seiten oder als Drachenviereck mit zwei parallelen Seitenpaaren bezeichnet werden.

Zusätzlich zu den gleich langen Seiten hat ein Rhombus noch weitere charakteristische Merkmale. Wenn ein Rhombus einen rechten Winkel besitzt, wird er zu einem Quadrat. Ein Quadrat ist somit eine spezielle Form des Rhombus.

Die Fläche eines Rhombus kann auf zwei verschiedene Arten berechnet werden. Eine Möglichkeit ist es, den Flächeninhalt als das halbe Diagonalenprodukt zu berechnen: A = (e * f) / 2. Alternativ kann der Flächeninhalt auch durch die Formel A = h * a bestimmt werden, wobei h die Höhe und a eine Seite des Rhombus ist.

Ein Rhombus hat außerdem die Eigenschaft, dass sich gegenüberliegende Winkel immer gleich groß sind. Dies bedeutet, dass die inneren Winkel des Rhombus paarweise gleich sind.

Zur Verdeutlichung können Schrägbilder verwendet werden, um die Geometrie eines Rhombus darzustellen.

Insgesamt zeichnet sich ein Rhombus also durch seine gleich langen Seiten und seine symmetrische Form aus. Er hat sowohl Eigenschaften eines Parallelogramms als auch eines Drachenvierecks und kann je nach spezifischen Merkmalen wie einem rechten Winkel sogar zu einem Quadrat werden.

Alles Wichtige über einen Rhombus

Eigenschaften eines Rhombus:

– Ein Rhombus ist ein Viereck, bei dem alle vier Seiten gleich lang sind.
– Ein Rhombus kann auch als Parallelogramm mit gleich langen Seiten oder als Drachenviereck mit zwei parallelen Seitenpaaren bezeichnet werden.
– Eine Raute mit einem rechten Winkel ist ein Quadrat.

Berechnung des Flächeninhalts:

– Den Flächeninhalt eines Rhombus kann man entweder wie beim Drachenviereck als das halbe Diagonalenprodukt berechnen: A = (e * f) / 2.
– Alternativ kann man den Flächeninhalt auch wie beim Parallelogramm als „Seite mal Höhe“ berechnen: A = h * a.

Anwendung in der Geometrie:

– Ein Rhombus kommt häufig in geometrischen Berechnungen vor, insbesondere wenn es um die Bestimmung von Flächeninhalten geht.
– Durch seine symmetrische Form und gleich langen Seiten hat der Rhombus bestimmte Eigenschaften, die ihn von anderen Vierecken unterscheiden.

Die Besonderheiten eines Rhombus erklärt

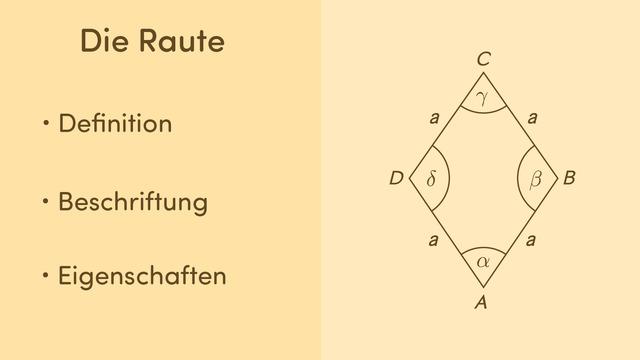
Definition und Eigenschaften

Ein Rhombus, auch Raute genannt, ist ein spezielles Viereck, bei dem alle vier Seiten gleich lang sind. Es handelt sich also um ein Parallelogramm mit gleich langen Seiten oder um ein Drachenviereck mit zwei parallelen Seitenpaaren. Eine weitere wichtige Eigenschaft der Raute ist, dass sie über gegenüberliegende Winkel verfügt, die gleich groß sind.

Berechnung des Flächeninhalts

Der Flächeninhalt einer Raute kann auf verschiedene Weisen berechnet werden. Zum einen kann er wie beim Drachenviereck als das halbe Diagonalenprodukt berechnet werden: A = (e * f) / 2. Dabei stehen e und f für die Längen der beiden Diagonalen der Raute. Alternativ kann der Flächeninhalt auch wie beim Parallelogramm als „Seite mal Höhe“ berechnet werden: A = h * a, wobei h die Höhe und a eine Seite der Raute darstellt.

Achsensymmetrie

Eine weitere interessante Eigenschaft eines Rhombus ist seine Achsensymmetrie. Das bedeutet, dass er punktsymmetrisch zur Mitte seiner Diagonalen ist. Das heißt, wenn man den Rhombus entlang einer seiner Diagonalen spiegelt, erhält man wieder den gleichen Rhombus.

Zusammenfassend lässt sich sagen, dass ein Rhombus ein besonderes Viereck mit gleich langen Seiten ist und über bestimmte symmetrische Eigenschaften verfügt. Der Flächeninhalt kann auf verschiedene Weisen berechnet werden und die Achsensymmetrie macht den Rhombus zu einem interessanten geometrischen Objekt.

Bedeutung und Charakteristika eines Rhombus

Ein Rhombus, auch bekannt als Raute, ist ein spezielles Viereck, bei dem alle vier Seiten gleich lang sind. Es kann auch als Parallelogramm mit gleich langen Seiten oder als Drachenviereck mit zwei parallelen Seitenpaaren bezeichnet werden. Ein besonderes Merkmal einer Raute ist, dass sie ein rechter Winkel sein kann. In diesem Fall wird die Raute zu einem Quadrat.

Ein Rhombus hat weitere Eigenschaften wie gleich große gegenüberliegende Winkel und den gleichen Flächeninhalt wie ein Parallelogramm oder Drachenviereck. Der Flächeninhalt kann entweder durch das halbe Diagonalenprodukt oder als „Seite mal Höhe“ berechnet werden.

Zusammenfassend lässt sich sagen, dass ein Rhombus ein Viereck ist, bei dem alle Seiten gleich lang sind und verschiedene Bezeichnungen haben kann. Es hat bestimmte geometrische Eigenschaften wie gleiche Winkel und einen bestimmten Flächeninhalt.

Ein Rhombus ist eine geometrische Figur mit vier gleich langen Seiten und gegenüberliegenden Winkeln, die ebenfalls gleich groß sind. Durch seine Symmetrie und Eigenschaften eignet sich ein Rhombus besonders gut für Berechnungen im mathematischen Bereich.