Erfolgreich Mathe lernen mit bettermarks: Antiproportionale Zuordnung erklärt

Eine antiproportionale Zuordnung beschreibt eine mathematische Beziehung, bei der zwei Größen umgekehrt proportional zueinander stehen. Das bedeutet, dass wenn eine Größe zunimmt, die andere abnimmt und umgekehrt. In diesem Artikel werden wir uns genauer mit dem Konzept der antiproportionalen Zuordnung befassen und seine Anwendung in verschiedenen Bereichen kennenlernen. Lassen Sie uns nun tiefer in dieses interessante Thema eintauchen!

Erklärung und Beispiele für eine antiproportionale Zuordnung

Eine antiproportionale Zuordnung liegt vor, wenn zwei Größen in umgekehrt proportionalem Verhältnis zueinander stehen. Das bedeutet, dass wenn eine Größe größer wird, die andere Größe kleiner wird und umgekehrt.

Ein Beispiel für eine antiproportionale Zuordnung ist die Geschwindigkeit eines Autos und die Zeit, die es benötigt, um eine bestimmte Strecke zurückzulegen. Wenn das Auto schneller fährt, benötigt es weniger Zeit, um die Strecke zu bewältigen. Umgekehrt braucht das Auto länger, wenn es langsamer fährt.

Eine weitere Beispiel ist der Zusammenhang zwischen Anzahl der Arbeiter und der Zeit, die benötigt wird, um eine Aufgabe abzuschließen. Wenn mehr Arbeiter an einer Aufgabe arbeiten, wird sie schneller erledigt sein. Wenn hingegen weniger Arbeiter eingesetzt werden, dauert es länger, bis die Aufgabe abgeschlossen ist.

In einer Wertetabelle einer antiproportionalen Zuordnung werden beide Größen dargestellt und ihre Werte miteinander verglichen. Dabei kann man beobachten, dass bei steigenden Werten einer Größe die Werte der anderen Größe abnehmen.

Ein Graph einer antiproportionalen Zuordnung zeigt eine Hyperbelkurve. Die Kurve verläuft von links oben nach rechts unten und hat den Scheitelpunkt im Ursprung (0/0). Je größer ein Wert auf der x-Achse ist, desto kleiner ist der entsprechende Wert auf der y-Achse.

Die adaptiven Übungen von bettermarks bieten Schülerinnen und Schülern die Möglichkeit, antiproportionale Zuordnungen interaktiv zu üben. Durch personalisierte Rückmeldungen können sie ihren Lernfortschritt verfolgen und gezielt an ihren Schwächen arbeiten.

Die wissenschaftliche Studie der Regierung von Uruguay hat gezeigt, dass die Nutzung von bettermarks zu einem Lernzuwachs von bis zu 30% führen kann. In Deutschland haben im Schuljahr 20/21 über 400.000 Schülerinnen und Schüler mit bettermarks gearbeitet und dabei mehr als 144 Millionen Aufgaben gelöst. Bettermarks wird in über zehn Ländern weltweit im Unterricht eingesetzt.

Bitte beachten Sie, dass auf der Website von bettermarks Cookies verwendet werden. Einige dieser Cookies sind essenziell für die Funktion der Website, während andere dazu dienen, die Erfahrung der Nutzer zu verbessern. Personenbezogene Daten können verarbeitet werden, zum Beispiel für personalisierte Anzeigen und Inhalte oder zur Messung von Anzeigen- und Inhaltsleistung. Weitere Informationen zur Verwendung Ihrer Daten finden Sie in der Datenschutzerklärung von bettermarks.

Impressum: [Impressum einfügen]

Merkmale und Eigenschaften einer antiproportionalen Zuordnung

1. Umgekehrt proportionale Beziehung

Eine antiproportionale Zuordnung liegt vor, wenn zwei Größen miteinander verknüpft sind und sich umgekehrt proportional zueinander verhalten. Das bedeutet, dass eine Größe größer wird, während die andere Größe kleiner wird, und umgekehrt. Wenn eine Größe verdoppelt wird, halbiert sich die andere Größe.

2. Wertetabelle

Um eine antiproportionale Zuordnung zu analysieren, kann eine Wertetabelle erstellt werden. Dabei werden verschiedene Werte für beide Größen festgelegt und ihre entsprechenden Werte berechnet. In einer antiproportionalen Zuordnung werden die Werte in der Regel nicht direkt proportional angegeben, sondern es ergibt sich ein bestimmtes Muster oder Verhältnis.

Beispiel:

Größe 1 | Größe 2
——–|——–
2 | 8
4 | 4
6 | 2

In diesem Beispiel wird deutlich, dass sich die Werte von Größe 1 umgekehrt proportional zu den Werten von Größe 2 verhalten.

3. Graphische Darstellung

Eine antiproportionale Zuordnung kann auch grafisch dargestellt werden. Dabei wird die erste Größe auf der x-Achse und die zweite Größe auf der y-Achse abgetragen. Die Punkte im Koordinatensystem ergeben dann einen Graphen, der eine Kurve bildet.

Bei einer antiproportionalen Zuordnung steigt der Graph zunächst steil an und flacht dann ab, je größer die Werte auf der x-Achse werden. Dies liegt daran, dass sich die beiden Größen umgekehrt proportional verhalten.

Zusammenfassend lässt sich sagen, dass antiproportionale Zuordnungen durch eine umgekehrte Proportionalität zwischen zwei Größen gekennzeichnet sind. Sie können mithilfe einer Wertetabelle oder graphischen Darstellung analysiert werden.

Wie funktioniert eine antiproportionale Zuordnung?

Definition

Eine antiproportionale Zuordnung ist eine mathematische Beziehung zwischen zwei Größen, bei der sich die Werte der einen Größe umgekehrt proportional zu den Werten der anderen Größe verhalten. Das bedeutet, dass wenn die Werte einer Größe steigen, die Werte der anderen Größe sinken und umgekehrt.

Beispiel

Ein einfaches Beispiel für eine antiproportionale Zuordnung ist die Geschwindigkeit und die Zeit. Nehmen wir an, ein Auto fährt mit konstanter Geschwindigkeit von 60 km/h. Wenn wir nun die Zeit betrachten, die das Auto benötigt, um eine bestimmte Strecke zurückzulegen, sehen wir folgendes Muster: Je länger das Auto unterwegs ist (also je größer die Zeit), desto weniger Strecke hat es in dieser Zeit zurückgelegt. Umgekehrt gilt auch: Je kürzer das Auto unterwegs ist (also je kleiner die Zeit), desto mehr Strecke hat es in dieser Zeit zurückgelegt.

Wertetabelle

Um eine antiproportionale Zuordnung darzustellen, kann man eine Wertetabelle verwenden. In dieser Tabelle werden jeweils Paare von Werten für beide Größen aufgelistet. Dabei kann man beobachten, dass wenn ein Wert größer wird, der andere Wert kleiner wird und umgekehrt.

Beispiel einer Wertetabelle für die Geschwindigkeit und Zeit:

| Zeit (in Stunden) | Geschwindigkeit (in km/h) |
|——————-|————————–|
| 1 | 60 |
| 2 | 30 |
| 3 | 20 |
| 4 | 15 |

Grafische Darstellung

Eine antiproportionale Zuordnung kann auch grafisch dargestellt werden. Dabei wird die eine Größe auf der x-Achse und die andere Größe auf der y-Achse abgetragen. In einem Koordinatensystem erhält man dann eine Hyperbel, bei der sich die Kurve immer weiter der y-Achse annähert, aber nie die Achse selbst berührt.

In unserem Beispiel mit Geschwindigkeit und Zeit würde die Grafik also eine nach unten geöffnete Hyperbel zeigen.

Zusammenfassend lässt sich sagen, dass eine antiproportionale Zuordnung eine Beziehung zwischen zwei Größen beschreibt, bei der sich die Werte umgekehrt proportional verhalten. Dies kann durch Wertetabellen oder grafische Darstellungen veranschaulicht werden.

Antiproportionale Zuordnungen: Definition und Anwendungsbeispiele

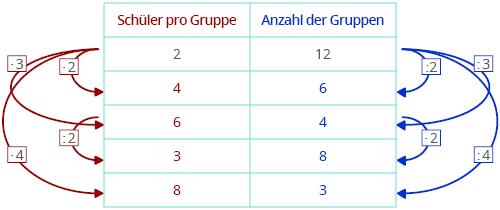
Definition:

Bei antiproportionalen Zuordnungen steht eine Größe in umgekehrtem Verhältnis zu einer anderen Größe. Das bedeutet, wenn eine Größe größer wird, wird die andere Größe kleiner und umgekehrt. In mathematischer Form kann dies durch die Gleichung y = k/x dargestellt werden, wobei k eine Konstante ist.

Anwendungsbeispiele:

– Ein Beispiel für eine antiproportionale Zuordnung ist die Zeit, die benötigt wird, um eine bestimmte Strecke zurückzulegen. Wenn die Geschwindigkeit erhöht wird, verringert sich die benötigte Zeit. Umgekehrt gilt: Wenn die Geschwindigkeit verringert wird, verlängert sich die benötigte Zeit.

– Ein weiteres Beispiel ist der Zusammenhang zwischen der Anzahl der Arbeiter und der Dauer eines Projekts. Je mehr Arbeiter an einem Projekt beteiligt sind, desto schneller kann das Projekt abgeschlossen werden. Wenn jedoch weniger Arbeiter zur Verfügung stehen, verlängert sich die Dauer des Projekts.

– In der Finanzwelt gibt es auch viele Beispiele für antiproportionale Zuordnungen. Zum Beispiel steht bei steigenden Zinssätzen die Höhe der monatlichen Ratenzahlungen für einen Kredit in umgekehrtem Verhältnis zur Laufzeit des Kredits. Je länger die Laufzeit des Kredits ist, desto niedriger sind die monatlichen Ratenzahlungen.

Diese Beispiele verdeutlichen den Zusammenhang zwischen antiproportionalen Zuordnungen und dem umgekehrten Verhältnis von Größen. Sie zeigen, wie sich eine Größe verändert, wenn die andere Größe variiert.

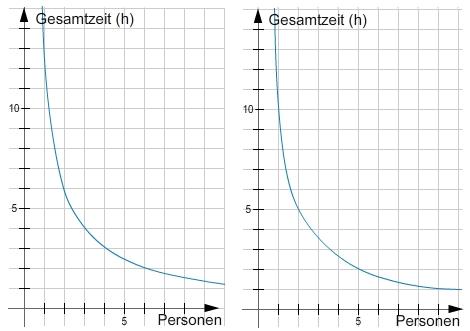
Graphen von antiproportionalen Zuordnungen: Erklärung und Interpretation

Antiproportionale Zuordnungen sind mathematische Beziehungen, bei denen eine Größe mit einer anderen umgekehrt proportional ist. Das bedeutet, dass wenn eine Größe größer wird, die andere entsprechend kleiner wird und umgekehrt. Die Beziehung zwischen den beiden Größen kann durch einen Graphen dargestellt werden.

Ein Graph einer antiproportionalen Zuordnung hat die Form einer Hyperbel. Die Hyperbel besteht aus zwei Ästen, die sich gegenüberliegen und sich der x- und y-Achse annähern, aber diese nie berühren oder schneiden. Der Graph verläuft also im ersten Quadranten oberhalb der x-Achse und im dritten Quadranten unterhalb der x-Achse.

Die Steigung des Graphen gibt an, wie stark die beiden Größen miteinander verknüpft sind. Je steiler der Graph abfällt, desto stärker ist die antiproportionale Beziehung zwischen den beiden Größen.

Die Interpretation des Graphen erfolgt anhand der Achsenbeschriftung. Die x-Achse repräsentiert eine Größe, während die y-Achse eine andere Größe darstellt. Wenn man entlang des Graphen nach rechts geht, nimmt die x-Größe zu und die y-Größe ab. Umgekehrt nimmt die x-Größe ab und die y-Größe zu, wenn man entlang des Graphen nach links geht.

Es ist wichtig zu beachten, dass ein linearer Zusammenhang zwischen den beiden Größen nicht vorliegt. Bei antiproportionalen Zuordnungen ändert sich das Verhältnis zwischen den beiden Größen, wenn eine von ihnen variiert.

Zusammenfassend kann gesagt werden, dass der Graph einer antiproportionalen Zuordnung die Beziehung zwischen zwei Größen darstellt, bei der eine Größe größer wird, während die andere kleiner wird. Der Graph hat die Form einer Hyperbel und die Steigung gibt Auskunft über die Stärke der Beziehung. Die Interpretation erfolgt entlang der Achsenbeschriftung.

Lernen mit bettermarks: Erfolgreich Mathe lernen, auch bei antiproportionalen Zuordnungen

Bettermarks bietet Schülerinnen und Schülern die Möglichkeit, Mathematik erfolgreich zu lernen, einschließlich des Themas der antiproportionalen Zuordnungen. Mit den adaptiven Übungen von bettermarks können Schülerinnen und Schüler auf verschiedenen Geräten wie Tablets, Computern und Smartphones rechnen und erhalten personalisierte Rückmeldungen.

Die Wirksamkeit von bettermarks wurde wissenschaftlich bewiesen. Die Regierung von Uruguay führte eine dreijährige Studie durch, basierend auf UNESCO-Daten zur Nutzung von bettermarks. Das Ergebnis zeigte einen Lernzuwachs von bis zu 30%. In Deutschland haben im Schuljahr 20/21 über 400.000 Schülerinnen und Schüler mit bettermarks gerechnet und dabei mehr als 144 Millionen Aufgaben gelöst.

Bettermarks wird in Schulen in über zehn Ländern weltweit eingesetzt, darunter Deutschland, die Niederlande, Uruguay und Südafrika. Es ist in vier Sprachen verfügbar und wird täglich im Unterricht verwendet.

In einer antiproportionalen Zuordnung verhalten sich zwei Größen umgekehrt proportional zueinander. Das bedeutet, dass eine Größe größer wird, während die andere kleiner wird, und umgekehrt. Dieses Verhältnis kann durch eine konstante Zahl beschrieben werden. Eine antiproportionale Zuordnung ist wichtig, um Beziehungen zwischen verschiedenen Variablen zu verstehen und sie mathematisch zu analysieren.