Pseudotetraden im BCD-Code ist ein interessantes Konzept, das in der digitalen Datenverarbeitung verwendet wird. Es bezieht sich auf eine spezielle Kombination von vier Bits, die bestimmte Zahlen repräsentieren können. Diese Methode ermöglicht eine effiziente und platzsparende Darstellung von dezimalen Zahlen im binären Format. In diesem Artikel werden wir näher darauf eingehen und die Funktionsweise sowie Anwendungen von Pseudotetraden im BCD-Code untersuchen.
- Verzaubere als Waldfee: Anleitung für selbstgemachtes Kostüm
- Wie Sie das Problem iPad nicht verfügbar beheben können – 3 einfache Methoden
- Optimales Alter für Winterreifen: Empfehlung von Continental
- Einfaches Rezept für selbstgemachtes Chiliöl – Schärfegrad nach Belieben
- Lidocain: Wirkung, Dosierung und Anwendungsgebiete
Bedeutung und Funktion von Pseudotetraden im BCD-Code
Die Pseudotetraden im BCD-Code haben keine Funktion und gehören nicht zu den eigentlichen Tetraden, die die Dezimalziffern repräsentieren. Sie werden auch als „falsche Tetraden“ bezeichnet. Im Gegensatz zu den echten Tetraden, die eine dezimale Wertigkeit haben, haben die Pseudotetraden keine spezifische Bedeutung oder Funktion.
Im BCD-Code werden nur 10 Tetraden benötigt, um die Dezimalziffern von 0 bis 9 darzustellen. Die übrigen 6 Tetraden sind Pseudotetraden und werden nicht verwendet. Sie dienen lediglich dazu, die Anzahl der Bits in einer binär codierten Dezimalzahl aufzufüllen.
In der Praxis werden jedoch andere Codes verwendet, da der BCD-Code sehr verschwenderisch ist und viel Speicherplatz benötigt. Die Verwendung von Pseudotetraden erhöht den Speicherbedarf weiter. Aus diesem Grund wird die BCD-Arithmetik selten angewendet und andere Codes bevorzugt.
Trotzdem gibt es Bereiche wie das Finanzwesen und die Wissenschaft, in denen eine hohe Genauigkeit erforderlich ist, die über die Gleitkommadarstellung hinausgeht. Hier kommen spezielle Codierungen wie das Densely Packed Decimal Encoding zum Einsatz.
In der Digitaltechnik und bei digitalen Anzeigen wie z.B. 7-Segment-Anzeigen wird jedoch immer noch häufig die BCD-Codierung verwendet. Um den BCD-Code als Dezimalzahl anzuzeigen, wird ein BCD-Decoder verwendet, der den Code auf die entsprechenden Segmente der 7-Segment-Anzeige umsetzt. Die Pseudotetraden haben dabei keine Funktion und werden nicht berücksichtigt.
Insgesamt sind die Pseudotetraden im BCD-Code also überflüssig und haben keine Bedeutung oder Funktion. Sie dienen lediglich dazu, die Anzahl der Bits in einer binär codierten Dezimalzahl aufzufüllen.
Die Rolle der Pseudotetraden im 8-4-2-1-BCD-Code erklärt
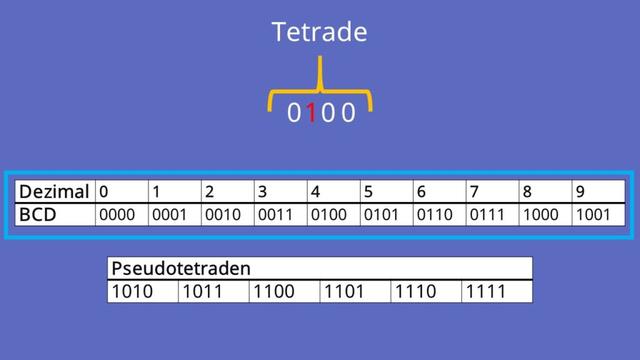
Im 8-4-2-1-BCD-Code werden die Dezimalziffern einer Dezimalzahl durch eigene 4-Bit-Dualzahlen dargestellt. Dabei stehen die Zahlen 8, 4, 2 und 1 für die dezimale Wertigkeit der dualen Stellen. Jede Dezimalziffer wird also durch eine Tetrade (eine Vierergruppe) von Bits repräsentiert.
Für die zehn Dezimalziffern werden nur zehn Tetraden benötigt. Die sechs weiteren Tetraden werden als Pseudotetraden bezeichnet und haben keine Funktion im BCD-Code. Sie entfallen oder dürfen nicht auftreten.
In der Praxis werden jedoch andere Codes verwendet, da der BCD zu verschwenderisch im Speicher ist. Auch bietet er gegenüber 32-Bit-Gleitkommazahlen nur eine etwas höhere Genauigkeit. Dennoch gibt es Bereiche wie das Finanzwesen und die Wissenschaft, in denen eine sehr hohe Genauigkeit gefordert ist, die über die Gleitkommadarstellung hinausgeht. Hier kommen spezielle Codierungen wie das Densely Packed Decimal Encoding zum Einsatz.
Die BCD-Codierung findet Anwendung in der Digitaltechnik und bei digitalen Anzeigen wie beispielsweise den 7-Segment-Anzeigen von Digitaluhren. Um den BCD-Code auf einer 7-Segment-Anzeige darstellen zu können, wird ein BCD-Decoder verwendet, der den 4-Bit-Dualcode auf die entsprechenden 7 Segmente umwandelt.
Die Pseudotetraden spielen in diesem Zusammenhang keine Rolle und werden daher nicht verwendet.
Warum Pseudotetraden im BCD-Code keine Funktion haben
Im BCD-Code werden Dezimalzahlen durch 4 Bit der entsprechenden dualen Zahl dargestellt. Für die 10 Dezimalziffern werden nur 10 Tetraden benötigt. Die restlichen 6 Tetraden, die als Pseudotetraden bezeichnet werden, gehören nicht mehr dazu und haben keine Funktion.
Die Pseudotetraden treten im BCD-Code nicht auf bzw. dürfen nicht auftreten. Sie sind überflüssig und führen zu einer verschwenderischen Nutzung des Speichers. Daher werden in der Praxis andere Codes verwendet, die effizienter sind.
BCD-Arithmetik wird heutzutage nur noch selten angewendet, da sie weniger effizient ist und gegenüber 32-Bit-Gleitkommazahlen nur eine geringfügig höhere Genauigkeit bietet. Dennoch gibt es Bereiche wie das Finanzwesen und die Wissenschaft, in denen eine sehr hohe Genauigkeit gefordert ist, die über die Gleitkommadarstellung hinausgeht.
Verwendung und Nutzen von Pseudotetraden im BCD-Code
Im BCD-Code werden Pseudotetraden verwendet, um dezimale Zahlen binär zu kodieren. Diese Pseudotetraden sind zusätzliche 4-Bit-Dualzahlen, die keine Funktion haben und im BCD-Code nicht auftreten dürfen. Sie dienen dazu, die Anzahl der benötigten Tetraden auf 10 zu begrenzen.
Der Nutzen von Pseudotetraden liegt darin, dass sie Platz sparen und den Speicher effizienter nutzen. Ohne sie würde für eine dreistellige Dezimalzahl von 0 bis 999 eine Dualzahl mit 10 Bit benötigt werden. Durch die Verwendung von Pseudotetraden kann die binäre Codierung auf 12 Bit reduziert werden.
Allerdings wird die BCD-Arithmetik aufgrund des verschwenderischen Speicherverbrauchs nur noch selten angewendet. Andere Codes, die weniger Platz benötigen, werden in der Praxis bevorzugt. Dennoch gibt es Bereiche wie das Finanzwesen und die Wissenschaft, in denen eine hohe Genauigkeit über die Gleitkommadarstellung hinaus erforderlich ist. Hier kommen spezielle Codierungen wie das Densely Packed Decimal Encoding zum Einsatz.
In der Digitaltechnik und bei digitalen Anzeigen findet die BCD-Codierung Verwendung. Zum Beispiel werden Digitaluhren im Innern mit dem BCD-Code betrieben. Auch die Uhrzeit im DCF77-Signal wird als BCD-Code kodiert.
Um den BCD-Code in Dezimalzahlen umzuwandeln und anzuzeigen, wird ein BCD-Decoder und eine 7-Segment-Anzeige verwendet. Der BCD-Decoder decodiert die 4-Bit-Dualzahlen auf die entsprechenden Segmente der Anzeige.
Die Verwendung von Pseudotetraden im BCD-Code ermöglicht eine effiziente binäre Darstellung von Dezimalzahlen und findet Anwendung in verschiedenen Bereichen der Elektronik.
Alternative Codes zur Vermeidung von Pseudotetraden im BCD-Code
Der BCD-Code hat den Nachteil, dass er Tetraden enthält, die keine Funktion haben und somit verschwendet sind. Aus diesem Grund werden in der Praxis alternative Codes verwendet, die effizienter sind.
Ein Beispiel für einen solchen alternativen Code ist der Excess-3-Code. Dabei handelt es sich um einen 4-Bit-Code, bei dem zu jeder Dezimalziffer 3 addiert wird. Dadurch entsteht eine Verschiebung um drei Stellen nach oben. Dieser Code vermeidet Pseudotetraden und wird häufig in der Digitaltechnik eingesetzt.
Ein weiterer alternativer Code ist der Gray-Code. Hierbei handelt es sich um einen binären Code, bei dem benachbarte Zahlen nur eine Bitänderung aufweisen. Dadurch wird verhindert, dass beim Übergang von einer Zahl zur nächsten mehrere Bits gleichzeitig geändert werden müssen. Der Gray-Code wird unter anderem in Drehgebern und analogen-digitalen Wandlern verwendet.
Es gibt noch weitere alternative Codes wie den 2421-Code oder den XS3-Code, die ebenfalls dazu dienen, Pseudotetraden zu vermeiden und die Effizienz der Codierung zu verbessern.
Diese alternativen Codes werden je nach Anwendungsbereich ausgewählt und eingesetzt, um eine optimale Darstellung und Verarbeitung von Zahlen zu gewährleisten.
Anwendungsgebiete, in denen Pseudotetraden im BCD-Code nicht auftreten dürfen
Anwendungsgebiete, in denen Pseudotetraden im BCD-Code nicht auftreten dürfen:
1. Finanzwesen: Im Finanzwesen ist eine hohe Genauigkeit bei der Darstellung und Verarbeitung von Zahlen erforderlich. Hier können Pseudotetraden im BCD-Code nicht auftreten, da sie zu Ungenauigkeiten führen würden. Daher werden spezielle Codes wie das Densely Packed Decimal Encoding verwendet, um eine präzise Repräsentation von Zahlen zu gewährleisten.
2. Wissenschaftliche Berechnungen: Auch in der Wissenschaft ist eine hohe Genauigkeit bei der Verarbeitung von Zahlen wichtig. Bei komplexen Berechnungen und Experimenten müssen genaue Ergebnisse erzielt werden. Daher dürfen auch hier keine Pseudotetraden im BCD-Code auftreten.
3. Digitale Anzeigen: In digitalen Anzeigen wie z.B. 7-Segment-Anzeigen wird der BCD-Code verwendet, um Zahlen darzustellen. Da diese Anzeigen eine hohe Genauigkeit erfordern, dürfen keine Pseudotetraden vorkommen, da dies zu falschen oder unlesbaren Anzeigen führen würde.
Es gibt jedoch auch Anwendungsgebiete, in denen die Verwendung von Pseudotetraden im BCD-Code akzeptabel ist, z.B. in weniger anspruchsvollen Bereichen der Digitaltechnik oder bei einfachen Rechenoperationen, bei denen eine geringere Genauigkeit ausreicht.
Zusammenfassend lässt sich sagen, dass Pseudotetraden im BCD-Code eine Methode zur Darstellung von Zahlen darstellen, bei der jede Ziffer in einer Gruppe von vier Bits codiert wird. Diese Technik ermöglicht die effiziente Speicherung und Verarbeitung von Dezimalzahlen in digitalen Systemen.

